국소 특이치 계수

Local outlier factor
시리즈의 일부
기계 학습
및 데이터 마이닝
Scatterplot featuring a linear support vector machine's decision boundary (dashed line)
문제
지도 학습
(분류 • 회귀)
클러스터링
치수 축소
구조화된 예측
이상 검출
인공신경망
강화 학습
인간과의 학습
모델 진단
이론.
기계학습장
관련 기사

이상 검출에서 Local Outlier Factor(LOF)는 Markus M. Breunig, Hans-Peter Kriegel, Raymond T에 의해 제안된 알고리즘입니다.Ng와 Jörg Sander는 2000년에 인접 [1]데이터 포인트에 대한 특정 데이터 포인트의 국소 편차를 측정하여 비정상적인 데이터 포인트를 찾아냈다.

LOF는 DBSCAN 및 Optics와 로컬 [2]밀도 추정에 사용되는 "코어 거리" 및 "도달 거리"의 개념과 같은 몇 가지 개념을 공유합니다.

기본 아이디어

LOF의 기본 개념: 한 점의 국소 밀도와 이웃의 밀도를 비교합니다.A의 밀도는 인접 라우터보다 훨씬 낮다.

로컬 특이치 인수는 로컬 밀도의 개념을 기반으로 하며, 여기서 가장 가까운 k개의 인접 라우터에 의해 로컬 밀도가 지정되며, 이 인접 라우터의 거리는 밀도를 추정하는 데 사용됩니다.물체의 로컬 밀도와 인접물체의 로컬 밀도를 비교함으로써 유사한 밀도의 영역과 인접물체보다 훨씬 낮은 밀도를 가진 점을 식별할 수 있습니다.이 값은 특이치로 간주됩니다.

국소 밀도는 한 지점이 인접 지점으로부터 "접근"될 수 있는 일반적인 거리로 추정됩니다.LOF에서 사용되는 "도달 가능 거리"의 정의는 군집 내에서 보다 안정적인 결과를 얻기 위한 추가 척도입니다.LOF가 사용하는 "도달 거리"에는 2차 출처(예: Ethem Alpaydin [3]교과서)에서 종종 부정확하게 발견되는 몇 가지 미묘한 세부 사항이 있다.

공식적인.

k-distance(A)는 물체 A에서 k번째 가장 가까운 이웃까지의 거리입니다.k개의 가장 가까운 네이버세트는 이 거리에 있는 모든 객체를 포함하며, "tie"의 경우 k개의 객체보다 클 수 있습니다.K개의 가장 가까운 네이버 세트를 N(A)으로 나타냅니다k.

도달 가능 거리 그림.오브젝트 B와 C의 도달 가능 거리(k=3)는 동일하지만, D는 k개의 가장 가까운 인접 라우터가 아닙니다.

이 거리는 도달 가능성 거리라고 불리는 것을 정의하기 위해 사용됩니다.

도달k 가능성 거리(A,B)=max{k-distance(B), d(A,B)}

즉, 물체 A와 물체 B의 도달 가능 거리는 두 물체의 실제 거리이지만 적어도 물체 B의 k 거리이다.B의 가장 가까운 인접 라우터 k개(B의 핵심, DBSCAN 클러스터 분석 참조)에 속하는 개체는 동일한 거리로 간주됩니다.이 거리를 두는 이유는 보다 안정적인[citation needed] 결과를 얻기 위해서입니다.이것은 대칭이 아니기 때문에 수학적 정의에서는 거리가 아닙니다.(항상 k-distance(A)를 사용하는 것은 일반적인[4] 실수이지만, 이것은 Simplified-LOF라고[4] 불리는 약간 다른 방법을 생성합니다.)

객체 A의 로컬 도달 가능성 밀도는 다음과 같이 정의됩니다.

lrdk(A):=1/(§ 도달가능성-거리B ∈ Nk(A)k(A, B)/ 없음k )

이것은 오브젝트 A가 네이버로부터의 평균 도달 가능 거리의 역수입니다.이것은 A로부터의 네이버의 평균 도달 가능성(정의로는 k-distance(A))이 아니라 A를 네이버로부터 「리치」할 수 있는 거리입니다.중복된 점을 사용하면 이 값은 무한대가 될 수 있습니다.

그런 다음 로컬 도달 가능성 밀도를 다음을 사용하는 네이버의 밀도와 비교합니다.

LOFk(A) : = LrdB ∈ Nk(A)kB ∈ Nk(A)k(B) / lrdk(A) / Nk(A) = Lrd(B) / Nk(A) · lrdk(A)

이는 네이버의 평균 로컬 도달 가능성 밀도를 객체 자체의 로컬 도달 가능성 밀도로 나눈 값입니다.값이 약 1이면 오브젝트가 네이버와 동등함을 나타냅니다(따라서 특이치가 아님).값이 1보다 작으면 밀도가 높은 영역(인사이어일 수 있음)을 나타내고 값이 1보다 크게 크면 특이치를 나타냅니다.

LOF(k)~1은 이웃과 비슷한 밀도를 의미합니다.

LOF(k) <1은 네이버보다 높은 밀도를 의미합니다(초기).

LOF(k) > 1은 네이버보다 밀도가 낮음을 의미합니다(이상).

이점

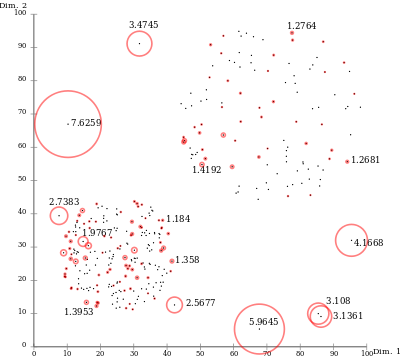
ELKI에 의해 시각화되는 LOF 점수.오른쪽 위 군집은 왼쪽 아래 군집에 가까운 특이치와 비슷한 밀도를 가지지만 특이치는 올바르게 탐지됩니다.

로컬 접근 방식 때문에 LOF는 데이터 집합의 다른 영역에서 특이치가 아닐 데이터 집합에서 특이치를 식별할 수 있습니다.예를 들어, 매우 조밀한 군집과 "작은" 거리에 있는 점은 특이치이지만, 희박한 군집 내의 점은 인접 군집과 유사한 거리를 나타낼 수 있습니다.

LOF의 기하학적 직관은 저차원 벡터 공간에만 적용 가능한 반면, 알고리즘은 유사성 함수를 정의할 수 있는 모든 맥락에서 적용될 수 있다.이는 수많은 설정에서 매우 잘 작동하며, [6]종종 네트워크 침입[5] 탐지 및 처리된 분류 벤치마크 데이터 등에서 경쟁업체를 능가하는 성능을 발휘하는 것으로 실험적으로 입증되었습니다.

LOF 계열의 메서드는 쉽게 일반화되어 지리 데이터, 비디오 스트림 또는 저작자 [4]네트워크의 이상 검출과 같은 기타 다양한 문제에 적용할 수 있습니다.

단점 및 확장 기능

결과 값은 몫 값이며 해석하기 어렵습니다.값이 1 이하일 경우 명확한 특이치를 나타내지만 점이 특이치일 경우 명확한 규칙이 없습니다.한 데이터 세트에서는 값 1.1이 이미 특이치일 수 있으며, 다른 데이터 세트에서는 값 2가 여전히 특이치일 수 있습니다.이러한 차이는 메서드의 인접성 때문에 데이터 집합 내에서 발생할 수도 있습니다.다음과 같은 측면에서 LOF보다 LOF의 확장이 있습니다.

  • Feature Bagging for Outlier[7] Detection은 여러 투영에서 LOF를 실행하고 그 결과를 결합하여 고차원에서의 검출 품질을 향상시킵니다.이것은 특이치 검출에 대한 첫 번째 앙상블 학습 접근법이며, 다른 변형은 [8]참조를 참조한다.
  • LoOP([9]Local Outlier Probability)는 LOF에서 파생된 방법이지만 저렴한 로컬 통계량을 사용하여 매개 변수 k의 선택에 덜 민감해집니다.또한 결과 값은 [0:1]의 값 범위로 스케일링됩니다.
  • 특이치[10] 점수 해석 및 통합은 LoOP 아이디어의 개선된 버전을 볼 수 있도록 통계적 척도를 사용하여 [0:1] 구간으로 LOF 특이치 점수를 정규화할 것을 제안한다.
  • 이상치 순위 및 이상치[11] 점수의 평가에서는 LOF 변종 및 기타 알고리즘을 사용하여 고급 이상치 검출 앙상블을 구축하고 위에서 설명한 기능 배깅 접근방식을 개선하기 위한 방법의 유사성과 다양성을 측정하는 방법을 제안한다.
  • 로컬 특이치 검출을 재검토: 공간, 비디오 및 네트워크 특이치[4] 검출에 응용한 로컬에 관한 일반적인 뷰에서는 다양한 로컬 특이치 검출 방법(LOF 및 LoOP의 단순화된 버전 포함)의 일반적인 패턴을 설명하고 이를 일반적인 프레임워크로 추상화합니다.그런 다음 이 프레임워크는 예를 들어 지리 데이터, 비디오 스트림 및 저작자 네트워크의 특이치 검출에 적용된다.

레퍼런스

  1. ^ Breunig, M. M.; Kriegel, H.-P.; Ng, R. T.; Sander, J. (2000). LOF: Identifying Density-based Local Outliers (PDF). Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. SIGMOD. pp. 93–104. doi:10.1145/335191.335388. ISBN 1-58113-217-4.
  2. ^ Breunig, M. M.; Kriegel, H.-P.; Ng, R. T.; Sander, J. R. (1999). "OPTICS-OF: Identifying Local Outliers" (PDF). Principles of Data Mining and Knowledge Discovery. Lecture Notes in Computer Science. Vol. 1704. p. 262. doi:10.1007/978-3-540-48247-5_28. ISBN 978-3-540-66490-1.
  3. ^ Alpaydin, Ethem (2020). Introduction to machine learning (Fourth ed.). Cambridge, Massachusetts. ISBN 978-0-262-04379-3. OCLC 1108782604.
  4. ^ a b c d Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). "Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection". Data Mining and Knowledge Discovery. 28: 190–237. doi:10.1007/s10618-012-0300-z. S2CID 19036098.
  5. ^ Lazarevic, A.; Ozgur, A.; Ertoz, L.; Srivastava, J.; Kumar, V. (2003). "A comparative study of anomaly detection schemes in network intrusion detection" (PDF). Proc. 3rd SIAM International Conference on Data Mining: 25–36. Archived from the original (PDF) on 2013-07-17. Retrieved 2010-05-14.{{cite journal}}:CS1 maint:작가들 매개 변수(링크)을 사용한다.
  6. ^ Campos, Guilherme O.; Zimek, Arthur; Sander, Jörg; Campello, Ricardo J. G. B.; Micenková, Barbora; Schubert, Erich; Assent, Ira; Houle, Michael E. (2016). "On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study". Data Mining and Knowledge Discovery. 30 (4): 891–927. doi:10.1007/s10618-015-0444-8. ISSN 1384-5810. S2CID 1952214.
  7. ^ Lazarevic, A.; Kumar, V. (2005). "Feature bagging for outlier detection". Proc. 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining: 157–166. doi:10.1145/1081870.1081891. ISBN 159593135X. S2CID 2054204.
  8. ^ Zimek, A.; Campello, R. J. G. B.; Sander, J. R. (2014). "Ensembles for unsupervised outlier detection". ACM SIGKDD Explorations Newsletter. 15: 11–22. doi:10.1145/2594473.2594476. S2CID 8065347.
  9. ^ Kriegel, H.-P.; Kröger, P.; Schubert, E.; Zimek, A. (2009). LoOP: Local Outlier Probabilities (PDF). Proceedings of the 18th ACM Conference on Information and Knowledge Management. CIKM '09. pp. 1649–1652. doi:10.1145/1645953.1646195. ISBN 978-1-60558-512-3.
  10. ^ Kriegel, H. P.; Kröger, P.; Schubert, E.; Zimek, A. (2011). Interpreting and Unifying Outlier Scores. Proceedings of the 2011 SIAM International Conference on Data Mining. pp. 13–24. CiteSeerX 10.1.1.232.2719. doi:10.1137/1.9781611972818.2. ISBN 978-0-89871-992-5.
  11. ^ Schubert, E.; Wojdanowski, R.; Zimek, A.; Kriegel, H. P. (2012). On Evaluation of Outlier Rankings and Outlier Scores. Proceedings of the 2012 SIAM International Conference on Data Mining. pp. 1047–1058. CiteSeerX 10.1.1.300.7205. doi:10.1137/1.9781611972825.90. ISBN 978-1-61197-232-0.