반전(이산수학)

컴퓨터 과학 및 이산 수학에서, 수열의 반전은 자연의 순서를 벗어난 한 쌍의 원소입니다.

정의들

반전

$【\displaystyle \pi】$를 치환이라고 합니다.중 만약 제가 <. j{\displaystyle i<, j}과π(나는)>π(j){\displaystyle \pi(나는)>, \pi)}, 장소의 쌍(나는, j){\displaystyle(i,j)}[1][2]이거나 원소의 쌍(π(나는),π(j)){\displaystyle{\bigl(}\pi(나는),\pi(j){\bigr)}}[3][4][5]π{\displayst의 자리 바꿈이라고 불린다.yle \pi}.

반전은 일반적으로 순열에 대해 정의되지만 시퀀스에 대해서도 정의할 수 있습니다.
S$(\displaystyle$ S$)$를 시퀀스(또는 멀티셋 순열^[6])로 $합니다{\displaystyle }$.i< \ $displaystyle$i < >$S$( )$>$S($j$ 의 $,{\displaystyle }$ 플레이스$($,$j )$의^[6][7] 쌍 또는 요소의${\displaystyle 쌍(}$ S (${\displaystyle i}$) ,${\displaystyle S}$ (${\displaystyle j}$)\ displaystyle $bigl ( s )$ 、 S \ J ( s ) 。

시퀀스의 경우 서로 다른 플레이스 쌍이 동일한 값의 쌍을 가질 수 있으므로 요소 기반 정의에 따른 반전은 고유하지 않습니다.

반전 세트는 모든 반전 세트입니다.장소 기반 정의에 따른 치환의 반전 세트는 요소 기반 정의에 따른 역치환의 반전 세트이며,^[9] 그 반대도 교환되는 쌍의 요소만으로 이루어집니다.

반전 번호

$시퀀스$ X의${\displaystyle }$$반전번호{\displaystyle \mathtt{}}$ ${\displaystyle \mathtt{in}}$v ( ${\displaystyle X}$$displaystyle$${$$inv}}(X))는$^[10] 반전세트의 카디널리티입니다$.$치환^[5] 또는 시퀀스의 ^[8](사전) 정렬 정도를 측정하는 일반적인 척도입니다.이 값은 0 ~$n{\displaystyle \frac{}{}}$(${\displaystyle \frac{}{\mathrm{}}}$ -${\displaystyle \frac{1}{}}$)$$2({$displaystyle {n(n-1)}{2}$포함$$) 사이로 구성됩니다.

$예$를 들어 ${\displaystyle \mathtt{i}}$ n ${\displaystyle \mathtt{v}}$(${\displaystyle 1}$1,${\displaystyle 2}$, ${\displaystyle \dots ,}$ ${\displaystyle n}$ ${\displaystyle ⟩}$ )$=$ ${\displaystyle 0}$ { $displaystyle${$inv$} （ \ $displaystyle 1$, 2$,$ $\ displayle , n$ \ $rangle$ ） $= 0$ } 。시퀀스가 정렬되어 있기 때문입니다.$또한$ ${\displaystyle \mathtt{v}}$(${\displaystyle }$+ ${\displaystyle 1}$,${\displaystyle }$n +${\displaystyle \mathrm{2개}}$ ${\displaystyle \dots ,}$ $,$ ${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle \dots ,}$ ${\displaystyle n}$ ${\displaystyle =}$ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ $(\$ $style$$$n$1,$ n$+2,\display,$ $, 2,\$display, $n$$rangle$)$=$ $^{$}$$이 마지막 예제는 직관적으로 정렬된 집합이 여전히 2차 반전을 가질 수 있음을 보여 줍니다.

이는 ^[9]순열의 화살표 다이어그램에 있는 교차 수, 동일 순열로부터의 켄달 타우 거리 및 아래에 정의된 각 반전 관련 벡터의 합입니다.

반전의 자리 기반 정의 또는 요소 기반 정의를 사용하여 반전 번호를 정의하든 상관없습니다. 왜냐하면 순열과 반전의 역수는 동일하기 때문입니다.

(사전) 정렬성의 다른 측정치에는 완전히 정렬된 시퀀스를 생성하기 위해 시퀀스에서 삭제할 수 있는 요소의 최소 수, 시퀀스 내에서 정렬된 "런"의 수와 길이, 스피어만 풋룰(정렬된 위치로부터의 각 요소의 거리 합), 시퀀스를 정렬하는 데 필요한 최소 교환 수가 포함됩니다.표준 비교 정렬 알고리즘은 시간 O(n log n)^[12]의 반전 수를 계산하기 위해 적용할 수 있다.^[11]

반전 관련 벡터

순열의 반전을 고유하게 결정하는 벡터로 압축하는 세 가지 유사한 벡터가 사용됩니다.이들은 종종 반전 벡터 또는 레머 코드라고 불립니다.(출처 목록은 여기서 찾을 수 있습니다.)

이 문서에서는 Wolfram과 ^[13]같이 반전 벡터($\displaystyle$ v$)$라는 용어를 사용합니다.나머지 2개의 벡터는 좌우 반전 벡터라고 불리기도 합니다만, 이 문서에서는 반전 벡터와의 혼동을 피하기 위해 좌반전 카운트($\displaystyle$ l$)$와 우반전 카운트($\displaystyle$ r$)$라고 부릅니다.요인 번호로 해석되는 왼쪽 반전 카운트는 순열 역콜렉소그래피를 ^[14]제공하고 오른쪽 반전 카운트는 사전 인덱스를 제공합니다.

반전 $벡터{\displaystyle }$ v$\displaystyle$ v$:$
요소 기반 $정의{\displaystyle }$ v$)$에서 {$displaystyle$ v$(i)}$는 작은(오른쪽) $컴포넌트$가 i${display$ i$\}$^[3]인 반전 수입니다.

${\displaystyle v}$( ${\displaystyle i}$) {$displaystyle$ v$(i)$ }는$$i$$ {$displaystyle$ i$\}$보다 큰 ${\$ {\$displaystyle$i$$$}$ 내의 요소의 수입니다.

$\displaystyle v(i)~=~\#\{k\mid k>i~\land~\pi^{-1}(k)<\pi^{-1)(i)\}}$

좌측 반전 $카운트{\displaystyle }$ l$\displaystyle$ l$:$
장소 기반 $정의{\displaystyle }$ l$)$에서 {$displaystyle$$l(i$$)\}$은 더 큰(오른쪽) 구성요소가$$i인 $반전{\displaystyle }$ $수입니다.$

${\displaystyle l}$${\displaystyle }$(${\displaystyle i}$) { $displaystyle$l ($i$ ) $($ ${\displaystyle 、}$（ i$$） { $displaystyle \pi$$}$$$( ( 、 ${\displaystyle （}$ ${\displaystyle i}$） { $displaystyle \pi （$ i ） $l$ $l{\displaystyle }$ l l l in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in

$\displaystyle l(i)~=~\#\left\{k\mid k<i~\land~\pi(k)>\pi(i)\right\}$

오른쪽 반전 $카운트{\displaystyle }$ r$\displaystyle$ r$.$ 흔히 Lemer 코드라고 불립니다.
장소 기반 정의${\displaystyle }r{\displaystyle }$ ( ${\displaystyle i}$) { $displaystyle$r ($i$ ) the$$ 、 작은 (왼쪽) 컴포넌트가$$i { $display i$}인 반전 수입니다.

${\displaystyle r}$${\displaystyle }$(${\displaystyle i}$) { $displaystyle$$$r ($i$ ) ${\displaystyle (}$ ${\displaystyle 、}$ （ ${\displaystyle i}$） {\ ( 、 （ i$$） { $displaystyle$ $\$$pi ( i$ )$$$r$ r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r （ i ) （ i$$ rdisplay r rdisplaydisplay \ \ \ \ \ \ \

$\displaystyle r(i)~=~\#{k\mid k>i~\land~\pi(k)<\pi(i)\}}$

$\$$displaystyle$$$v와$$ $\displaystyle$$$r은 모두$$ Rothe 다이어그램의 도움을 받아 찾을 수 있습니다.$R{\displaystyle }$($i)$는 1s가 점으로 표시된 치환 매트릭스이며, 오른쪽과 아래에 점이 있는 모든 위치에 반전(종종종 십자 표시)을 나타냅니다.r$i)$은 회전의 역합입니다.w $w{\displaystyle }$i ( $displaystyle$i )는 Rothe 다이어그램의 $i$입니다.$v$(${\displaystyle i}$ $)$ { $displaystyle$v ($i$ ) i$$ i 、 i$の$i i w w w 。역행렬의 치환행렬은 $전치$입니다$.$따라서$치환$의 v\$displaystyle$ v는$역행렬$의 r\$displaystyle$이며, 그 반대의 경우도 마찬가지입니다.

예:4개 요소의 모든 순열

다음 정렬 가능한 표는 4개 요소의 24개의 순열과 그 자리 기반 반전 세트, 반전 관련 벡터 및 반전 번호를 보여줍니다. (작은 열은 옆에 있는 열의 반사이며 총체적 순서로 정렬하는 데 사용할 수 있습니다.)

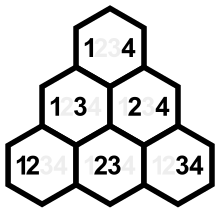
$\displaystyle$v와$$ $\displaystyle$l은$$ 항상 같은 자리수를 가지며 l$\displaystyle$$l$과 r$\displaystyle$r은$$ 둘 다 플레이스 베이스 반전 세트와 관련되어 있음을 $알{\displaystyle }$ 수 있습니다.l$${\$displaystyle$ l$}$의 $중요$한 요소는 표시된 삼각형의 내림대각선의 합계이며 r {\$displaystyle r}$의 요소는 오름대각선의 합계입니다.(내림대각선의 페어는 공통적으로 오른쪽 컴포넌트 2, 3, 4를 가지며, 오름대각선의 페어는 왼쪽 컴포넌트 1, 2, 2, 3 c를 가집니다).OMMON)

테이블의 기본 순서는 "\$displaystyle\pi$에 의한 역콜렉스 순서입니다.이것은 l$\backslash$$displaystyle$l에 $의한{\displaystyle }$ colex 순서와 동일합니다.\$displaystyle \pi }$에 의한 렉스 순서는 r$\displaystyle$r에 $의한{\displaystyle }$ 렉스 순서와 동일합니다.

비교를 위한 3차원 순열
0 1 2 3 4 5 $\displaystyle \pi }$ ${\displaystyle v}$ $(\displaystyle l)$ p-b ${\displaystyle r}$ # 0 123 321 000. 000. 000. 000. 000. 000. 0 1 213 312 백 001 010 010 백 001 1 2 132 231 010 010 백 001 010 010 1 3 312 213 110 011 110 011 이백 002 2 4 231 132 이백 002 이백 002 110 011 2 5 321 123 210 012 210 012 210 012 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

$\displaystyle \pi }$ ${\displaystyle v}$ $(\displaystyle l)$ p-b ${\displaystyle r}$ # 0 1234 4321 0000 0000 0000 0000 0000 0000 0 1 2134 4312 천 0001 0010 0100 천 0001 1 2 1324 4231 0100 0010 0100 0010 0100 0010 1 3 3124 4213 1100 0011 0110 0110 2000년 0002 2 4 2314 4132 2000년 0002 0200 0020 1100 0011 2 5 3214 4123 2100 0012 0210 0120 2100 0012 3 6 1243 3421 0010 0100 천 0001 0010 0100 1 7 2143 3412 1010 0101 1010 0101 1010 0101 2 8 1423 3241 0110 0110 1100 0011 0200 0020 2 9 4123 3214 1110 0111 1110 0111 3000 0003 3 10 2413 3142 2010년 0102 1200 0021 1200 0021 3 11 4213 3124 2110 0112 1210 0121 3100 0013 4 12 1342 2431 0200 0020 2000년 0002 0110 0110 2 13 3142 2413 1200 0021 2010년 0102 2010년 0102 3 14 1432 2341 0210 0120 2100 0012 0210 0120 3 15 4132 2314 1210 0121 2110 0112 3010 0103 4 16 3412 2143 2200 0022 2200 0022 2200 0022 4 17 4312 2134 2210 0122 2210 0122 3200 0023 5 18 2341 1432 3000 0003 3000 0003 1110 0111 3 19 3241 1423 3100 0013 3010 0103 2110 0112 4 20 2431 1342 3010 0103 3100 0013 1210 0121 4 21 4231 1324 3110 0113 3110 0113 3110 0113 5 22 3421 1243 3200 0023 3200 0023 2210 0122 5 23 4321 1234 3210 0123 3210 0123 3210 0123 6

약한 순열 순서

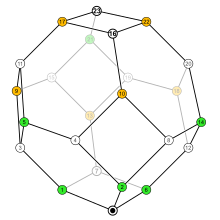
n개 항목의 순열 집합은 격자를 형성하는 순열의 약한 순서라고 하는 부분 차수의 구조를 제공할 수 있습니다.

부분집합 관계에 의해 순서가 매겨진 반전 집합의 Hasse 다이어그램은 분면체의 골격을 형성합니다.

자리 기반 정의를 사용하여 각 반전 세트에 순열을 할당하면 순열의 순서는 순열의 순서가 됩니다. 여기서 가장자리는 연속된 값을 가진 두 요소의 스왑에 해당합니다.이것은 순열의 약한 순서입니다.아이덴티티는 최소값이고, 아이덴티티를 반전시킴으로써 형성되는 치환율은 최대값입니다.

요소 기반 정의를 사용하여 각 반전 세트에 순열을 할당한 경우 결과 순열의 순서는 케일리 그래프의 순열 순서가 됩니다. 케일리 그래프에서는 가장자리가 연속된 위치에서 두 요소의 스왑에 해당합니다.대칭 그룹의 이 케일리 그래프는 각 순열이 그 반전으로 대체된 것과 유사합니다.

「 」를 참조해 주세요.

• 요인 번호 체계
• 치환 그래프
• 이행, 심플 이행, 반전 및 정렬
• 다메라우-레벤슈테인 거리
• 치환의 패리티

OEIS 시퀀스:

• 요인 기준 표현과 관련된 시퀀스
• 요인 번호:A007623 및 A108731
• 반전 번호:A034968
• 이진수로 해석되는 유한 순열의 반전 집합: A211362(관련 순열: A211363)
• 반전 벡터에 0과 1만 있는 유한 순열:A059590(반전 세트: A211364)
• k개의 반전이 있는 n개의 원소의 순열 수; Mahonian 수:A008302(각 행의 최대값, Kendall-Mann 번호:A000140)
• n개의 에지와 n개의 노드가 있는 연결된 레이블이 지정된 그래프 수:A057500

레퍼런스

출처 문헌 목록

추가 정보

사전 정렬성 측정