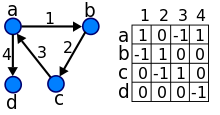
유향 그래프

수학, 특히 그래프 이론에서, 방향 그래프(directed graph)는 호라고 불리는 방향 모서리에 의해 연결된 정점의 집합으로 구성된 그래프이다.

정의.

공식 용어로 유향 그래프는 순서 쌍 G = (V, A)이다^[1].

• V는 요소를 정점, 노드 또는 점이라고 하는 집합입니다.
• A는 호, 방향 모서리(때로는 A 대신 E라는 이름의 해당 세트가 있는 단순한 가장자리), 화살표 또는 방향 선으로 구성된 정점 쌍의 집합입니다.

이는 보통 또는 무방향 그래프와 달리 후자는 보통 가장자리, 링크 또는 선이라고 불리는 정점의 순서가 없는 쌍으로 정의된다는 점에서 다릅니다.

전술한 정의에서는, 같은 소스 노드와 타겟 노드를 가지는 복수의 화살표가 유향 그래프에 있는 것은 허가되지 않습니다만, 일부의 저자는, 유향 그래프에 그러한 복수의 호를 가지는 것을 가능하게 하는 광범위한 정의를 고려하고 있습니다(즉, 호 세트를 멀티셋으로 하는 것을 허가합니다).보다 구체적으로 말하면, 이러한 엔티티는 유향 멀티그래프(또는 멀티그래프)로서 취급됩니다.
한편, 전술한 정의에서는, 유향 그래프에 루프(즉, 노드와 직접 접속하는 호)를 설정할 수 있지만, 일부 저자는 유향 그래프에 ^[2]루프를 설정할 수 없는 좁은 정의를 고려하고 있습니다.보다 구체적으로 루프가 없는 방향 그래프는 단순한 방향 그래프로 처리되며, 루프가 있는 방향 그래프는 루프 방향 그래프로 처리된다(섹션 방향 그래프의 유형 참조).

방향 그래프의 종류

서브클래스

• 대칭 방향 그래프는 모든 가장자리가 양방향인 방향 그래프입니다(즉, 이그래프에 속하는 모든 화살표에 대해 대응하는 반전 화살표도 이 그래프에 속함).
• 단순 방향 그래프는 루프가 없고(정점을 직접 연결하는 화살표) 소스 노드와 대상 노드가 동일한 여러 개의 화살표가 없는 방향 그래프입니다.이미 소개한 바와 같이, 여러 화살표가 있는 경우, 엔티티는 일반적으로 방향 다중 그래프로 처리됩니다.일부 저자는 루프가 있는 디그래프를 루프 ^[2]디그래프라고 표현합니다.
  • 완전한 방향 그래프는 각 정점의 쌍이 대칭적인 방향 호 쌍으로 결합되는 단순한 방향 그래프입니다(이것은 가장자리가 역호 쌍으로 대체되는 방향 없는 전체 그래프와 동일합니다).따라서 완전한 이중 그래프는 대칭이다.
  • 반완전 다층 디그래프는 정점 집합이 다른 부분 집합의 모든 정점 x와 y 쌍에 대해 x와 y 사이에 호가 존재하도록 부분 집합으로 분할된 단순한 디그래프입니다.x와 y 사이에 하나의 호가 있을 수도 있고 반대 방향으로 두 개의 호가 있을 수도 있습니다.^[3]
  • 반완전 이중그래프는 각 정점 쌍 사이에 호가 있는 단순한 이중그래프입니다.모든 반완전 디그래프는 반완전 다층 디그래프이며, 여기서 정점의 수는 부분 집합의 수와 같습니다.^[4]
  • 준추이형 디그래프는 x에서 y로, 그리고 y에서 z로 호가 있는 서로 다른 정점의 3중 x, y, z에 대해 x와 z 사이에 호가 있는 단순한 디그래프입니다.x와 z 사이에 하나의 호만 있을 수도 있고 반대 방향으로 두 개의 호만 있을 수도 있습니다.반완전 이중그래프는 준전이성 이중그래프이다.k-준-반-반-반-반-반-반-반-반-반-반이라는 반-반-반-반-반-반-반-반-반-반-반-반-^[5]
  • 방향 그래프는 양방향 에지가 없는 방향 그래프이다(즉, (x, y) 및 (y, x) 중 최대 하나는 그래프의 화살표일 수 있다).따라서 방향 그래프는 2-사이클이 ^[6]없는 경우에만 방향 그래프입니다.
    • 토너먼트는 무방향 완전 그래프에서 각 에지에 대한 방향을 선택하여 얻은 방향 그래프입니다.토너먼트는 반완전 디그래프입니다.^[7]
    • 방향 비순환 그래프(DAG)는 방향 ^[8]주기가 없는 방향 그래프입니다.
      • 멀티트리는 단일 시작 정점에서 서로 다른 두 방향 경로가 동일한 끝 정점에서 다시 만나지 않는 DAG입니다.
      • 지향성 트리 또는 폴리트리는 무방향 비순환 그래프의 가장자리를 지향하여 형성된 DAG입니다.
        • 루트 트리는 기본 무방향 트리의 모든 가장자리가 루트에서 멀리 또는 루트로 향하는 방향성 트리입니다(각각 아웃트리와 인트리라고 불립니다).

보조 특성이 있는 디그래프

이 목록은 불완전합니다. 누락된 항목을 추가하여 도움을 줄 수 있습니다.(2016년 8월)

• 가중치 유도 그래프(유향 네트워크라고도 함)는 가중치 그래프(무방향 네트워크 또는 가중치 ^[2]네트워크라고도 함)와 마찬가지로 화살표에 가중치가 할당된 (단순한) 유도 그래프입니다.
  • 플로우 네트워크는 송신원과 싱크라는2개의 노드가 구별되는 가중치 유향 그래프입니다.
• 루트 방향 그래프(흐름 그래프라고도 함)는 정점이 루트로 구분된 이그래프입니다.
  • 제어 흐름 그래프는 컴퓨터 과학에서 프로그램을 실행하는 동안 통과할 수 있는 경로의 표현으로 사용되는 루트 디그래프입니다.
• 신호 흐름 그래프는 노드가 시스템 변수를 나타내고 분기(에지, 호 또는 화살표)가 노드 쌍 간의 기능 연결을 나타내는 방향 그래프입니다.
• 흐름 그래프는 일련의 선형 대수 방정식 또는 미분 방정식과 연관된 이중 그래프입니다.
• 상태 다이어그램은 유한 상태 머신을 나타내는 방향 멀티그래프입니다.
• 가환 다이어그램은 범주 이론에서 사용되는 이중그래프이며, 여기서 정점은 (수학적인) 객체를 나타내고 화살표는 형태소를 나타냅니다. 시작과 끝점이 동일한 방향 경로가 구성에 의해 동일한 결과를 초래한다는 특성을 가집니다.
• 매복하여 단체의 이론, 전율의 도메인으로는 통제된 그래프, 한일의 모양, 표현을 V는 functor로 정의되는 함수 기호 범주 FinVctKF(Q)Q에 F(Q) 않고 범주 유한 차원의. 벡터 공간의 Q와 FinVctK은 범주에서 경로로 구성된 구체적으로는 개체는 자연성. 에 대한필드 K흔들림의 표현은 벡터 공간과 그 가장자리(및 경로)로 정점에 라벨을 붙이고 그 사이의 선형 변환과 호환되며 자연 변환을 통해 변환됩니다.

기본 용어

호(x, y)는 x에서 y로 향하는 것으로 간주되며, y는 선두, x는 호 꼬리, y는 x의 직접 후계자, x는 y의 직접 이전인 것으로 간주됩니다.경로가 x에서 y로 이어지는 경우 y는 x의 후속이며 x에서 도달 가능하다고 하며 x는 y의 선행이라고 합니다.호(y, x)를 (x, y)의 역호라고 합니다.

루프가 있는 멀티지그래프의 인접행렬은 정점에 대응하는 행과 열이 있는 정수값 행렬입니다.여기서 비대각 엔트리_ij a는 정점 i에서 정점 j까지의 호수이고 대각 엔트리_ii a는 정점 i에서의 루프수입니다.방향 그래프의 인접 행렬은 행과 열의 동일한 순열까지 고유합니다.

유향 그래프에 대한 또 다른 행렬 표현은 발생 행렬이다.

자세한 정의는 방향을 참조하십시오.

인데그리와 아웃도

정점의 경우, 정점에 인접한 머리끝의 수는 정점의 독립이라고 불리며, 정점에 인접한 꼬리끝의 수는 정점의 이탈(나무의 분기 계수라고 불린다)입니다.

G = (V, A) 및 v µ V로 하자.v의 인데리는 deg(v)로⁻ 표시되며, outdeg(v)는 deg⁺(v)

deg(v) = 0인⁻ 정점은 각각의 나오는 호의 원점이기 때문에 소스라고 불린다.마찬가지로, deg(v) = 0인⁺ 정점은 들어오는 호 각각이 끝이기 때문에 싱크라고 불린다.

도합 공식은 유향 그래프에 대해 다음과 같이 기술합니다.

$\displaystyle \sum _{v\in V}\deg ^{-}(v)=\sum _{v\in V}\deg ^{+}(v)= A .}$

모든 정점 v δ V, deg⁺(v) = deg⁻(v)에 대해 그래프는 균형 지향 ^[9]그래프라고 불린다.

도순서

유향 그래프의 도수열은 해당 도수와 외도 쌍의 목록입니다. 위의 예에서는 도수열((2, 0), (2, 2) (0, 2) (1, 1)이 있습니다.정도 시퀀스는 방향 그래프 불변성이므로 동형 방향 그래프는 동일한 정도 시퀀스를 가집니다.그러나 정도 시퀀스는 일반적으로 방향 그래프를 고유하게 식별하지 않는다. 어떤 경우, 비동형 이중 그래프는 같은 정도 시퀀스를 가진다.

유향 그래프 실현 문제는 주어진 양의 정수 쌍의 시퀀스를 갖는 유향 그래프를 찾는 문제입니다.(유향 그래프에 적절한 수의 고립된 정점을 추가함으로써 3차적으로 실현되기 때문에 0의 트레일링 쌍은 무시될 수 있습니다.)유향 그래프의 정도 순서인 순서, 즉 유향 그래프 실현 문제가 해결책을 가지고 있는 것을 유향 그래픽 또는 유향 그래픽 시퀀스라고 한다.이 문제는 클라이트만-왕 알고리즘 또는 풀커슨-첸-안스티 정리로 해결할 수 있다.

방향 그래프 연결

그래프의 모든 방향 에지를 방향 없는 에지로 대체하여 얻은 방향 없는 기본 그래프가 연결된 그래프일 경우 방향 그래프는 약하게 연결되어 있다(또는 그냥 연결되어^[10] 있다).

방향 그래프는 모든 정점 쌍(x, y)에 대해 x에서 y(및 y에서 x)까지의 방향 경로를 포함하는 경우 강하게 연결되거나 강하게 연결됩니다.강한 구성요소는 가장 강하게 연결된 하위 그래프입니다.

연결된 루트 그래프(또는 흐름 그래프)는 구별된 루트 정점에서 모든 정점으로 향하는 방향 경로가 존재하는 그래프입니다.

「 」를 참조해 주세요.

메모들

레퍼런스

• Bang-Jensen, Jørgen; Gutin, Gregory (2000), Digraphs: Theory, Algorithms and Applications, Springer, ISBN 1-85233-268-9
  (2007년 개정판 제1판은 저자의 사이트에서 무료로 입수할 수 있습니다.제2판은 2009년 ISBN1-84800-997-6에 게재되었습니다).
• 를 클릭합니다Bang-Jensen, Jørgen; Gutin, Gregory (2018), Classes of Directed Graphs, Springer, ISBN 3319718401.
• 를 클릭합니다Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7.
• Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6 (전자 제3판은 저자의 사이트에서 무료로 입수할 수 있습니다.
• 를 클릭합니다Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley.
• 온라인 정수 시퀀스 백과사전에서 n개의 노드가 있는 방향 그래프(또는 방향 그래프)의 수

외부 링크