반복 재구성

Iterative reconstruction
필터링된 백투영법(오른쪽 절반)과 반복 재구성 방법(왼쪽 절반) 간의 차이를 보여주는 예제

반복 재구성은 특정 영상 기술에서 2D 및 3D 영상을 재구성하는 데 사용되는 반복 알고리즘을 말합니다.예를 들어, 컴퓨터 단층 촬영에서는 객체의 투영으로부터 영상을 재구성해야 합니다.여기서 반복 재구성 기법은 일반적으로 단일 재구성 [1]단계에서 영상을 직접 계산하는 공통 필터링된 역투영(FBP) 방법보다 더 낫지만 계산적으로 더 비싸다.최근의 연구에서 과학자들은 반복적인 재구성을 위해 매우 빠른 연산과 거대한 병렬화가 가능하다는 것을 보여주었고, 이것은 반복적인 재구성을 상용화에 [2]실용화한다.

기본 개념

반복 재구성(왼쪽)과 필터링된 백투영(오른쪽)을 사용한 CT 스캔

획득된 데이터에서 영상을 재구성하는 것은 역문제입니다.종종, 그 역문제를 정확히 직접 푸는 것은 불가능하다.이 경우 직접 알고리즘은 솔루션에 근사해야 하며, 이로 인해 영상에 눈에 보이는 재구성 아티팩트가 발생할 수 있습니다.반복 알고리즘은 여러 반복 단계를 사용하여 올바른 솔루션에 접근하므로 더 높은 계산 시간을 들여 더 나은 재구성을 얻을 수 있습니다.

다양한 알고리즘이 있지만 각각 가정된 이미지에서 시작하여 이미지에서 투영을 계산하고 원래 투영 데이터를 비교하여 계산된 투영과 실제 투영 간의 차이에 따라 이미지를 업데이트합니다.

대수적 재구성

주요 기사:대수적 재구성 기법

대수 재구성 기법(ART)은 하운스필드에 의해 컴퓨터 단층촬영에 사용된 최초의 반복 재구성 기법이었다.

반복 스파스 점근 최소 분산

주요 기사: SAMV (알고리즘)

반복적 스파스 점근 최소 분산 알고리즘은 합성 장비 레이더, 컴퓨터 단층 촬영 스캔 및 자기 공명 영상(MRI)의 애플리케이션을 사용하여 압축 감지에서 영감을 얻은 파라미터가 없는 반복적인 초고해상도 단층 촬영 재구성 방법입니다.

통계 재구성

통계 반복 영상 재구성 알고리즘에는 일반적으로 5가지 구성 요소가 있습니다.[3]

  1. 데이터에서 추정해야 하는 미지의 계수를 갖는 유한 계열로 재구성해야 하는 미지의 연속 함수 f { f를 표현하는 객체 모델.
  2. 측정 노이즈가 없을 때 녹음되는 "이상적인" 측정과 미지의 물체를 관련짓는 시스템 모델.대부분의 경우 이 은 A +{\(\ 의 선형 모델입니다.여기서 은 노이즈를 나타냅니다.
  3. 잡음 측정값이 이상적인 값 주변에서 어떻게 달라지는지를 설명하는 통계 모형입니다.종종 가우스 노이즈 또는 포아송 통계량이 가정됩니다.포아송 통계량은 현실에 가깝기 때문에 더 널리 사용됩니다.
  4. 영상 계수 벡터를 추정하기 위해 최소화하는 비용 함수입니다.대부분의 경우 이 비용 함수에는 일정한 형태의 정규화가 포함됩니다.때때로 정규화는 마르코프 랜덤 필드에 기초한다.
  5. 일반적으로 반복적인 것으로, 이미지의 초기 추정치와 반복 종료를 위한 정지 기준을 포함한 비용 함수를 최소화하기 위한 알고리즘입니다.

학습된 반복 재구성

학습된 반복 재구성에서 업데이트 알고리즘은 이미지 형성 모델을 포함하면서 컨볼루션 뉴럴 네트워크와 같은 기계 학습 기술을 사용하여 훈련 데이터로부터 학습된다.이는 일반적으로 보다 빠르고 고품질의 재구성을 제공하며 CT 및 MRI [5]재구성에 적용되어[4] 왔습니다.

이점

사람의 심장에 대한 실시간 MRI(rt-MRI) 영상의 단일 프레임. a) 직접 재구성 b) 반복(비선형 역) 재구성[6]

반복적 접근법의 장점은 노이즈에 대한 둔감성 향상과 불완전한 데이터의 경우 최적의 이미지를 재구성하는 능력이다.이 방법은 SPECT 및 PET와 같은 방사 단층 촬영 방식에 적용되었으며, 광선 경로를 따라 상당한 감쇠가 발생하고 노이즈 통계는 상대적으로 빈약하다.

통계적, 우도 기반 접근법: 통계적, 우도 기반 반복 기대 최대화 알고리즘은[7] 현재 재구성에 선호되는 방법이 되었다.그러한 알고리즘은 종종 FBP에 공통적인 소음 프로파일과 스트릭 아티팩트에 대한 내성을 제공하고, 통계 원리에 기초하여 측정된 데이터로 이어진 소멸 사건의 가능한 분포 추정치를 계산한다.방사성 추적기의 밀도는 함수공간의 함수이므로 매우 고차원적이기 때문에 최대우도 솔루션을 패널티 방식 또는 최대 a-사후방법으로 전환하는 방법은 낮은 계수에 대해 상당한 이점을 가질 수 있다.Ulf Grenander의 Sieve 추정기[9][10] 또는 Bayes 패널티 [11][12]방법과 같은 예 또는 I.J. Good의 거칠기 방법은[13][14] 포아송 우도 함수만을 포함하는 기대 최대화 기반 방법보다 우수한 성능을 산출할 수 있다.

또 다른 예로, 사용할 수 있는 큰 투영 세트가 없거나, 투영된 각도가 균일하게 분포되지 않거나, 투영된 부분이 특정 방향으로 희박하거나 누락된 경우 더 우수한 것으로 간주됩니다.이러한 시나리오는 수술 중 CT, 심장 CT 또는 금속[15][16] 아티팩트에서 투영 데이터의 일부를 제외해야 하는 경우에 발생할 수 있습니다.

자기 공명 영상에서 그것과 multiple과 견본 추출 패턴이 기존의 데카르트 grid[17]에서 다른 일을 하면서 코일을 받는 데이터으로부터 이미지들을 재건하고 개선된 조절 기술의 사용(예를 들어 총 변이)[18]또는 물리적 processes[19]의 확장 모델은 reconstru해 지는 것 사용될 수 있다.불완전.예를 들어 반복 알고리즘을 사용하면 실시간 MRI(rt-MRI)[6]에 필요한 대로 매우 짧은 시간에 획득한 데이터에서 영상을 재구성할 수 있습니다.

하드웨어 한계로 인해 제한된 수의 투영을 획득하고 생물학적 시료 손상을 방지하기 위해 Cryo Electron Tomography에서 압축 감지 기술 또는 정규화 기능(예: Huber 기능)과 함께 사용하여 더 나은 [20]해석을 위한 재구성을 개선할 수 있습니다.

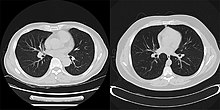
다음은 심장 [21]MRI에 대한 반복 영상 재구성의 이점을 보여주는 예입니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Herman, G. T., 컴퓨터 단층 촬영의 기초: 투영으로부터의 이미지 재구축, 제2판, Springer, 2009년
  2. ^ Wang, Xiao; Sabne, Amit; Kisner, Sherman; Raghunathan, Anand; Bouman, Charles; Midkiff, Samuel (2016-01-01). High Performance Model Based Image Reconstruction. Proceedings of the 21st ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. PPoPP '16. New York, NY, USA: ACM. pp. 2:1–2:12. doi:10.1145/2851141.2851163. ISBN 9781450340922. S2CID 16569156.
  3. ^ Fessler J A (1994). "Penalized weighted least-squares image reconstruction for positron emission tomography" (PDF). IEEE Transactions on Medical Imaging. 13 (2): 290–300. doi:10.1109/42.293921. hdl:2027.42/85851. PMID 18218505.
  4. ^ Adler, J.; Öktem, O. (2018). "Learned Primal-dual Reconstruction". IEEE Transactions on Medical Imaging. PP (99): 1322–1332. arXiv:1707.06474. doi:10.1109/tmi.2018.2799231. ISSN 0278-0062. PMID 29870362. S2CID 26897002.
  5. ^ Hammernik, Kerstin; Klatzer, Teresa; Kobler, Erich; Recht, Michael P.; Sodickson, Daniel K.; Pock, Thomas; Knoll, Florian (2018). "Learning a variational network for reconstruction of accelerated MRI data". Magnetic Resonance in Medicine. 79 (6): 3055–3071. arXiv:1704.00447. doi:10.1002/mrm.26977. ISSN 1522-2594. PMC 5902683. PMID 29115689.
  6. ^ a b Uecker M, Zhang S, Voit D, Karaus A, Merboldt KD, Frahm J (2010a). "Real-time MRI at a resolution of 20 ms" (PDF). NMR Biomed. 23 (8): 986–994. doi:10.1002/nbm.1585. hdl:11858/00-001M-0000-0012-D4F9-7. PMID 20799371. S2CID 8268489.
  7. ^ Carson, Lange; Richard Carson (1984). "EM reconstruction algorithm for emission and transmission tomography". Journal of Computer Assisted Tomography. 8 (2): 306–316. PMID 6608535.
  8. ^ Vardi, Y.; L. A. Shepp; L. Kaufman (1985). "A statistical model for positron emission tomography". Journal of the American Statistical Association. 80 (389): 8–37. doi:10.1080/01621459.1985.10477119.
  9. ^ Snyder, Donald L.; Miller, Michael I. (1985). "On the Use of the Method of Sieves for Positron Emission Tomography". IEEE Transactions on Medical Imaging. NS-32(5) (5): 3864–3872. Bibcode:1985ITNS...32.3864S. doi:10.1109/TNS.1985.4334521. S2CID 2112617.
  10. ^ Snyder, D.L.; Miller, M.I.; Thomas, L.J.; Politte, D.G. (1987). "Noise and edge artifacts in maximum-likelihood reconstructions for emission tomography". IEEE Transactions on Medical Imaging. 6 (3): 228–238. doi:10.1109/tmi.1987.4307831. PMID 18244025. S2CID 30033603.
  11. ^ Geman, Stuart; McClure, Donald E. (1985). "Bayesian image analysis: An application to single photon emission tomography" (PDF). Proceedings Amererican Statistical Computing: 12–18.
  12. ^ Green, Peter J. (1990). "Bayesian Reconstructions for Emission Tomography Data Using a Modified EM Algorithm". IEEE Transactions on Medical Imaging. 9 (1): 84–93. CiteSeerX 10.1.1.144.8671. doi:10.1109/42.52985. PMID 18222753.
  13. ^ Miller, Michael I.; Snyder, Donald L. (1987). "The role of likelihood and entropy in incomplete data problems: Applications to estimating point-process intensites and toeplitz constrained covariance estimates". Proceedings of the IEEE. 5 (7): 3223–3227. doi:10.1109/PROC.1987.13825. S2CID 23733140.
  14. ^ Miller, Michael I.; Roysam, Badrinath (April 1991). "Bayesian image reconstruction for emission tomography incorporating Good's roughness prior on massively parallel processors". Proceedings of the National Academy of Sciences of the United States of America. 88 (8): 3223–3227. Bibcode:1991PNAS...88.3223M. doi:10.1073/pnas.88.8.3223. PMC 51418. PMID 2014243.
  15. ^ Wang, G.E.; Snyder, D.L.; O'Sullivan, J.A.; Vannier, M.W. (1996). "Iterative deblurring for CT metal artifact reduction". IEEE Transactions on Medical Imaging. 15 (5): 657–664. doi:10.1109/42.538943. PMID 18215947.
  16. ^ Boas FE, Fleischmann D (2011). "Evaluation of two iterative techniques for reducing metal artifacts in computed tomography". Radiology. 259 (3): 894–902. doi:10.1148/radiol.11101782. PMID 21357521. Archived from the original on 2011-12-01.
  17. ^ Pruessmann K. P., Weiger M., Börnert P., Boesiger P. (2001). "Advances in sensitivity encoding with arbitrary k-space trajectories". Magnetic Resonance in Medicine. 46 (4): 638–651. doi:10.1002/mrm.1241. PMID 11590639.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  18. ^ Block K. T., Uecker M., Frahm J. (2007). "Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint". Magnetic Resonance in Medicine. 57 (6): 1086–1098. doi:10.1002/mrm.21236. hdl:11858/00-001M-0000-0012-E2A3-7. PMID 17534903. S2CID 16396739.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  19. ^ Fessler J (2010). "Model-based Image Reconstruction for MRI". IEEE Signal Processing Magazine. 27 (4): 81–89. Bibcode:2010ISPM...27...81F. doi:10.1109/msp.2010.936726. PMC 2996730. PMID 21135916.
  20. ^ Albarqouni, Shadi; Lasser, Tobias; Alkhaldi, Weaam; Al-Amoudi, Ashraf; Navab, Nassir (2015-01-01). Gao, Fei; Shi, Kuangyu; Li, Shuo (eds.). Gradient Projection for Regularized Cryo-Electron Tomographic Reconstruction. Lecture Notes in Computational Vision and Biomechanics. Springer International Publishing. pp. 43–51. doi:10.1007/978-3-319-18431-9_5. ISBN 978-3-319-18430-2.
  21. ^ I Uyanik, P Lindner, D Shah, N Tsekos I Pavliidis (2013) 자유호흡 및 비동기 심장 MRI에서의 생리학적 운동 해결을 위한 레벨 세트 방법 적용. FIMH, 2013,

[1] [2]

Wikimedia Commons에는 반복 재구성과 관련된 미디어가 있습니다.
  1. ^ Bruyant P.P. (2002). "Analytic and iterative reconstruction algorithms in SPECT". Journal of Nuclear Medicine. 43 (10): 1343–1358. PMID 12368373.
  2. ^ Grishentcev A. Jr (2012). "Effective compression of images on the basis of differential analysis" (PDF). Journal of Radio Electronics. 11: 1–42.