힐버트 큐브

수학에서, 데이비드 힐버트의 이름을 딴 힐버트 큐브는 위상에서 일부 사상의 교훈적인 예를 제공하는 위상학적 공간이다.게다가, 많은 흥미로운 위상학적 공간들이 힐버트 큐브에 내장될 수 있다; 즉, 힐버트 큐브의 하위공간으로 볼 수 있다(아래 참조).

정의

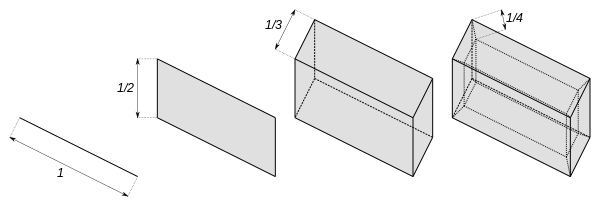
Hilbert 큐브는 n = 1, 2, 3, 4, ...에 대한 [0, 1/n] 구간의 위상학적 산물로 가장 잘 정의된다.즉, 무한 치수의 큐보이드로서, 각 직교 방향의 가장자리 길이가 시퀀스${\displaystyle }${ ${\displaystyle 1}$/ n ${\displaystyle {}_{}}$ ${\displaystyle {n\mathbb{}}_{}}$ ${\displaystyle {\in }_{}}$ N ${\$1$/n\rbrace _{n\in \mathb{N}}}}}}}$를 형성한다$.$

Hilbert 큐브는 단위 간격의 무한히 많은 복사본의 산물에 대해 동형이다[0, 1].다시 말해, 그것은 토폴로지적으로 무한한 차원의 단위 큐브와 구분할 수 없다.

If a point in the Hilbert cube is specified by a sequence ${\displaystyle \lbrace a_{n}\rbrace }$ with ${\displaystyle 0\leq a_{n}\leq 1/n}$, then a homeomorphism to the infinite dimensional unit cube is given by ${\displaystyle h(a)_{n}=n\cdot a_{n}}$.

미터법 공간으로서의 힐버트 큐브

때로는 힐버트 큐브를 미터법 공간, 실제로 분리 가능한 힐버트 공간의 특정 부분집합(즉, 셀 수 없이 무한히 힐버트 기반이 있는 힐버트 공간)으로 생각하는 것이 편리하다.이러한 목적을 위해서는 [0,1]의 사본의 산물이라고 생각하지 말고, 대신 [0,1]이라고 생각하는 것이 가장 좋다.

[0,1] × [0,1/2] × [0,1/3] × ···;

위와 같이 위상학적 특성에 대해서는, 이것은 아무런 차이가 없다.즉, 힐버트 큐브의 원소는 무한 시퀀스다.

(x_n)

만족하는

0_n ≤ x ≤ 1/n

그러한 순서는 모두 힐버트 공간 to에₂ 속하므로 힐버트 큐브는 거기서 미터법을 계승한다.메트릭에 의해 유도되는 위상이 위의 정의에서 제품 위상과 동일하다는 것을 보여줄 수 있다.

특성.

콤팩트한 하우스도르프 공간의 산물로서 힐버트 큐브 자체가 타이코노프 정리 결과 컴팩트한 하우스도르프 공간이다.힐버트 큐브의 소형성은 힐버트 큐브에 설정된 일반적인 칸토어로부터 연속적인 함수를 구성함으로써 선택의 악시오머 없이도 증명될 수 있다.

ℓ에서₂, 어떤 포인트도 콤팩트한 이웃을 가지고 있지 않다(따라서, ℓ은₂ 국소적으로 콤팩트하지 않다).ℓ의₂ 콤팩트 서브셋은 모두 유한한 차원이라고 기대할 수 있다.힐버트 큐브는 이것이 사실이 아님을 보여준다.그러나 힐버트 큐브는 각각의 치수에서 옆면이 점점 작아지기 때문에 어떤 점 p의 이웃이 되지 못하므로 고정 반지름 e > 0의 p 주위에 있는 열린 공은 어떤 치수에서 큐브 바깥으로 나가야 한다.

$l{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}의 임의의 무한 차원 볼록 콤팩트 부분집합은$$ 힐버트 큐브와 동형이다.힐버트 큐브는 볼록한 세트인데, 그 스팬은 전체 공간이지만 내부는 비어 있다.이런 상황은 유한한 차원에서는 불가능하다.0 벡터의 큐브에 대한 접선 원뿔은 전체 공간이다.

힐버트 큐브의 모든 부분 집합은 힐버트 큐브로부터 메트리징 가능(그리고 따라서 T4)과 두 번째 카운트 가능성의 특성을 상속받는다.그 반대의 경우도 다음과 같이 하는 것이 더 흥미롭다.1초마다 계산 가능한 T4 공간은 힐버트 큐브 부분집합에 대해 동형이다.

힐버트 큐브의 모든 G-subset은_δ 분리 가능하고 완전한 미터법 공간에 대한 위상학적 공간 동형질인 폴란드 공간이다.반대로, 모든 폴란드 공간은 힐버트 큐브의 G-subset에_δ 대해 동형이다.^[1]

메모들

참조

• Srivastava, Shashi Mohan (1998). A Course on Borel Sets. Graduate Texts in Mathematics. Springer-Verlag. ISBN 978-0-387-98412-4. Retrieved 2008-12-04.
• "Die Homoiomorphie der kompakten konvexen Mengen im Hilbertschen Raum" [The homomorphism of the compact convex sets in Hilbert space] (in German). EUDML. Archived from the original on 2020-03-02.

추가 읽기

• Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology (Dover reprint of 1978 ed.). Berlin, New York: Springer-Verlag. ISBN 978-0-486-68735-3. MR 0507446.