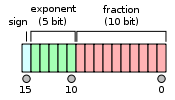
반정밀 부동소수점 형식

Half-precision floating-point format
다른 16비트 부동소수점 형식인 bfloat16과 혼동하지 마십시오.

컴퓨팅에서 하프 정밀도(FP16이라고도 함)는 컴퓨터 메모리에서 16비트(현대 컴퓨터에서는 2바이트)를 차지하는 이진 부동 소수점 컴퓨터 번호 형식입니다.특히 영상 처리 및 신경 네트워크와 같은 더 높은 정밀도가 필요하지 않은 애플리케이션에서 부동 소수점 값을 저장하기 위한 것입니다.

현대의 거의 모든 용도는 IEEE 754-2008 표준에 준거하고 있습니다.여기서 16비트 base-2 형식은 binary16으로 불리며 지수는 5비트를 사용합니다.이 값은 ±65,504 범위의 값을 나타낼 수 있으며, 1 이상의 최소값은 1 + 1/1024입니다.

컴퓨터에 따라서는 반정밀이 2배 정밀도보다 훨씬 더 빠를 수 있습니다.예를 들어, 1개의 클라우드 [1]프로바이더에서는 반정밀의 경우 550PFLOPS, 2배 정밀도의 경우 37PFLOPS 등입니다.

부동 소수점 포맷
IEEE 754
다른.

역사

1982년 히타치의 HD61810 DSP[2], Scott의 WIF[3] 및 3dfx Voodoo Graphics [4]프로세서를 포함한 몇 가지 초기 16비트 부동소수점 포맷이 존재했습니다.

ILM은 싱글 또는 더블 정밀 부동소수점의 [5]하드 드라이브 및 메모리 비용을 들이지 않고 광범위한 다이내믹 레인지를 처리할 수 있는 이미지 포맷을 찾고 있었습니다.SGI(Silicon Graphics)의 John Airey가 이끄는 하드웨어 가속 프로그램 가능 음영 그룹은 1997년 '발리' 설계 노력의 일환으로 s10e5 데이터 유형을 발명했습니다.이는 SIGGRAPH 2000[6] 논문(섹션 4.3 참조)에 기술되어 있으며, 미국 특허 7518615에 더욱 문서화되어 있습니다.[7]오픈 소스 OpenEXR 이미지 포맷을 사용하여 대중화되었습니다.

Nvidia와 Microsoft는 2002년 초에 출시된 Cg 언어로 하프 데이터형을 정의하고 2002년 [8]말에 출시된 GeForce FX의 실리콘으로 구현했습니다.그 후 그래픽 카드에서의 16비트 부동소수점 연산 지원은 매우 [citation needed]보편화되었습니다.

2012년 F16C 확장에 따라 x86 프로세서는 기계 명령에 따라 반정밀 플로트를 단정밀 플로트로 변환할 수 있습니다.

IEEE 754 반정밀 바이너리 부동소수점 형식: binary16

IEEE 754[9] 표준에서는 binary16 의 형식은 다음과 같습니다.

형식은 다음과 같이 배열되어 있습니다.

IEEE 754r Half Floating Point Format.svg

이 형식은 지수 필드가 모두 0으로 저장되지 않는 한 값이 1인 암묵적인 리드 비트를 갖는 것으로 가정합니다.따라서 메모리 형식으로 표시되는 것은 의 10비트뿐이지만 전체 정밀도는 11비트입니다.IEEE 754 용어로 10비트의 유효와 정밀도가 있습니다만, 11비트의 유효와 정밀도가 있습니다(log1011(2) 3 3.311의 소수점 이하, 또는 마지막 자리에서는4 자리 ± 5 단위보다 약간 작은 값).

지수 부호화

반정밀 바이너리 부동소수점 지수는 오프셋-바이너리 표현을 사용하여 부호화되며 제로 오프셋은 15입니다.IEE 754 표준에서는 지수 바이어스라고도 불립니다.

  • Emin = 000012 - 011112 = -14
  • Emax = 111102 - 011112 = 15
  • 지수 치우침 = 011112 = 15

따라서 오프셋 이진 표현에 의해 정의된 대로 실제 지수를 얻으려면 저장된 지수에서 오프셋 15를 빼야 합니다.

저장된 지수 000002 및 11111은2 특별히 해석됩니다.

지수 유의 및 = 0 유의와 zero 0 방정식
000002 제로, -0 정규 이하의 수 (-1)signbit × 2−14 × 0. 비트2
000012, ..., 111102 정규화 값 (-1)signbit × 2exponent−15 × 1. 비트2
111112 ±160 NaN(저소음, 시그널링)

최소 엄밀하게 양의 값(비정규값)은−24 2 5 5.96 × 10이다−8.최소 양의 정규값은 2 6 6.10 × 10이다−14−5.최대 대표 값은 (2-2−10) × 215 = 65504입니다.

반정밀 예시

다음 예는 부동소수점 값의 비트 표현으로 제시되어 있습니다.여기에는 부호 비트, (바이어스) 지수 및 significant가 포함됩니다.

바이너리 16진수 가치 메모들
0 00000 0000000000 0000 0
0 00000 0000000001 0001 2−14 × (0 +)1/140) 0 0.000000059604645 최소 양수 미정규수
0 00000 1111111111 03ff 2−14 × (0 + 1023 / 1024 ) 0 0.000060975552 최대 정규 미만수
0 00001 0000000000 0400 2−14 × (1 + 0/10) ≈ 0.00006103515625 최소 정규수
0 01101 0101010101 3555 2−2 × (1 + 341 / 1 000 ) 0 0.33325195 1/3에 가장 가까운 값
0 01110 1111111111 스리프 2−1 × (1 + 1023 / 1024 ) 0 0 . 99951172 1보다 작은 최대수
0 01111 0000000000 3c00 20 × (1 + 0/160 ) = 1 하나.
0 01111 0000000001 3c01 20 × (1 + 1/1/1,000 ) ) 1.0009765 1보다 큰 최소수
0 11110 1111111111 7 bff 215 × (1 + 1023 / 1024 ) = 65504 최대 정규수
0 11111 0000000000 7시 ∞ 무궁무한
1 00000 0000000000 8000 −0
1 10000 0000000000 c000 -2
1 11111 0000000000 fc00 −∞ 음의 무한대

디폴트로는 1/3은 2배 정밀도의 경우와 같이 반올림합니다.이는 유의한 비트 수가 홀수이기 때문입니다.반올림점 너머의 비트는 0101...꼴찌 단위의 1/2보다 작습니다.

정밀도 제한

분 맥스. 간격
0 2개−13 2개−24
2개−13 2개−12 2개−23
2개−12 2개−11 2개−22
2개−11 2개−10 2개−21
2개−10 2개−9 2개−20
2개−9 2개−8 2개−19
2개−8 2개−7 2개−18
2개−7 2개−6 2개−17
2개−6 2개−5 2개−16
2개−5 2개−4 2개−15
2개−4 1/8 2개−14
1/8 1/4 2개−13
1/4 1/2 2개−12
1/2 1 2개−11
1 2 2개−10
2 4 2개−9
4 8 2개−8
8 16 2개−7
16 32 2개−6
32 64 2개−5
64 128 2개−4
128 256 1/8
256 512 1/4
512 1024 1/2
1024 2048 1
2048 4096 2
4096 8192 4
8192 16384 8
16384 32768 16
32768 65519 32
65519 ∞ ∞

65519는 유한수(65504)로 반올림하는 최대수이며 65520 이상은 무한대로 반올림합니다.이것은 반올림에서 반올림 전략으로 이 컷오프를 변경한다.

ARM 대체 반정밀

ARM 프로세서는 (부동소수점 제어 레지스터 비트를 통해) "대체 하프 정밀도" 형식을 지원하므로 지수 값 31(11112)[10]에 대한 특수 케이스가 필요하지 않습니다.IEEE 형식과 거의 동일하지만 infinity 또는 NaN 인코딩은 없습니다.대신 31의 지수는 65536 ~131008 범위의 정규화된 번호를 인코딩합니다.

반정밀 사용

이 형식은 MATLAB, OpenEXR, JPEG XR, GIMP, OpenGL, Cg, Direct3D, D3DX 등의 여러 컴퓨터 그래픽 환경에서 픽셀을 저장하기 위해 사용됩니다.8비트 또는 16비트 정수에 비해 동적 범위가 증가하여 이미지의 하이라이트 및 음영에 더 자세한 내용을 보존할 수 있고 명암을 선형으로 표현하여 계산이 쉬워진다는 장점이 있습니다.32비트 단정도 부동소수점 대비 장점은 스토리지와 대역폭의 절반(정밀도와 범위를 희생)[5]이 필요하다는 것입니다.

머신러닝이나 뉴럴 네트워크용 하드웨어나 소프트웨어는 반정밀을 사용하는 경향이 있습니다.이러한 어플리케이션은 보통 많은 양의 계산을 실시하지만 높은 수준의 정밀도를 필요로 하지 않습니다.

하드웨어에 반정밀 연산 명령이 있는 경우 단정도 또는 배정도 연산보다 빠릅니다.시스템에 하나의 명령으로 여러 부동소수점 숫자를 처리할 수 있는 SIMD 명령이 있는 경우,[11] 동시에 2배의 숫자로 동작함으로써 반정밀도를 2배로 높일 수 있습니다.단, 하드웨어 지원이 없는 경우 에뮬레이션 또는 단일 또는 이중 정밀도로 변환한 후 되돌리는 방식으로 계산해야 하므로 속도가 느립니다.

하드웨어 지원

ARM 아키텍처의 일부 버전은 반정밀을 [12]지원합니다.

x86 명령어 세트의 반정밀 지원은 AVX-512_FP16 명령어 세트 확장에 기재되어 있습니다.향후 인텔 Sapire Rapids [13]프로세서에 실장될 예정입니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ "About ABCI - About ABCI ABCI". abci.ai. Retrieved 2019-10-06.
  2. ^ "hitachi :: dataBooks :: HD61810 Digital Signal Processor Users Manual". Archive.org. Retrieved 2017-07-14.
  3. ^ Scott, Thomas J. (March 1991). "Mathematics and Computer Science at Odds over Real Numbers". SIGCSE '91 Proceedings of the Twenty-Second SIGCSE Technical Symposium on Computer Science Education. 23 (1): 130–139. doi:10.1145/107004.107029. ISBN 0897913779. S2CID 16648394.
  4. ^ "/home/usr/bk/glide/docs2.3.1/GLIDEPGM.DOC". Gamers.org. Retrieved 2017-07-14.
  5. ^ a b "OpenEXR". OpenEXR. Retrieved 2017-07-14.
  6. ^ Mark S. Peercy; Marc Olano; John Airey; P. Jeffrey Ungar. "Interactive Multi-Pass Programmable Shading" (PDF). People.csail.mit.edu. Retrieved 2017-07-14.
  7. ^ "Patent US7518615 - Display system having floating point rasterization and floating point ... - Google Patents". Google.com. Retrieved 2017-07-14.
  8. ^ "vs_2_sw". Cg 3.1 Toolkit Documentation. Nvidia. Retrieved 17 August 2016.
  9. ^ IEEE Standard for Floating-Point Arithmetic. IEEE STD 754-2019 (Revision of IEEE 754-2008). July 2019. pp. 1–84. doi:10.1109/ieeestd.2019.8766229. ISBN 978-1-5044-5924-2.
  10. ^ "Half-precision floating-point number support". RealView Compilation Tools Compiler User Guide. 10 December 2010. Retrieved 2015-05-05.
  11. ^ Ho, Nhut-Minh; Wong, Weng-Fai (September 1, 2017). "Exploiting half precision arithmetic in Nvidia GPUs" (PDF). Department of Computer Science, National University of Singapore. Retrieved July 13, 2020. Nvidia recently introduced native half precision floating point support (FP16) into their Pascal GPUs. This was mainly motivated by the possibility that this will speed up data intensive and error tolerant applications in GPUs.
  12. ^ "Half-precision floating-point number format". ARM Compiler armclang Reference Guide Version 6.7. ARM Developer. Retrieved 13 May 2022.
  13. ^ Towner, Daniel. "Intel® Advanced Vector Extensions 512 - FP16 Instruction Set for Intel® Xeon® Processor Based Products" (PDF). Intel® Builders Programs. Retrieved 13 May 2022.

추가 정보

외부 링크