자유 부울 대수

수학에서 자유 부울대수는 다음과 같은 생성기라 불리는 원소의 구별된 집합을 가진 부울대수다.

부울 대수의 각 요소는 부울 연산을 사용하여 발전기의 유한 조합으로 표현할 수 있다.
어떤 원소를 선택하든 모든 부울 대수에서 보유하지 않는 (부울 연산을 사용한 유한 표현식의 측면에서) 그들 사이에 관계가 없다는 점에서 발전기는 가능한 한 독립적이다.

간단한 예

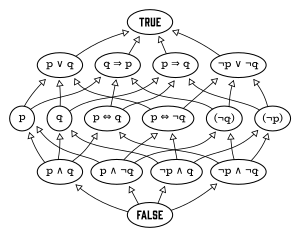
The Hasse diagram of the free Boolean algebra on two generators, p and q. Take p (left circle) to be "John is tall" and q (right circle)to be "Mary is rich". The atoms are the four elements in the row just above FALSE.

자유 부울대수의 생성자는 독립적 명제를 대표할 수 있다.예를 들어, "존은 키가 크다"와 "메리는 부자다"라는 명제를 생각해 보자.이들은 네 개의 원자로 부울 대수를 생성하는데, 즉 다음과 같다.

존은 키가 크고, 메리는 부자다.
존은 키가 크고, 메리는 부유하지 않다.
존은 키가 크지 않고, 메리는 부자다.
존은 키가 크지 않고, 메리는 부유하지 않다.

부울대수의 다른 요소들은 "존은 키가 크고 메리는 부유하지 않다" 또는 "존은 키가 크지 않고 메리는 부자다"와 같은 원자의 논리적 분열을 말한다.게다가 FALSE라는 원소가 하나 더 있는데, 이것은 공허한 분리, 즉 원자가 없는 분리라고 생각할 수 있다.

이 예는 16개의 원소를 가진 부울대수를 산출한다. 일반적으로 유한 n의 경우, n개의 발전기를 가진 자유부울대수는 2개의ⁿ 원자를 가지며, 따라서 $2^{2^{n}}$ $2^{2^{n}}$ ${\$ 2 $^{2^{n}}$ 의 $2^{2^{n}}$ 원소를 가진다.

발전기가 무한히 많으면 지금 원자가 없다는 점을 제외하면 비슷한 상황이 우세하다.부울 대수의 각 요소는 논리적으로 등가라면 동일한 것으로 간주되는 두 개의 그러한 요소를 갖는 생성 명제들의 정밀하게 많은 조합이다.

n-요소 집합의 자유 부울대수가 2 $2^{2^{n}}$ ${\$ 2 $^{2^{n}}$ 요소를 $2^{2^{n}}$ 갖는 이유를 알 수 있는 또 다른 방법은 각 원소가 n비트에서 1비트까지의 함수라는 점에 주목하는 것이다.이러한 기능에 $2^{n}$ ${\$ 가능한 $2^{n}$ 입력이 있으며, 각 입력에 대해 출력하려면 함수가 0 또는 1을 선택하므로 2 $2^{2^{n}}$ ${\$ 2 $^{2^{n}}}$ 가능한 $2^{2^{n}}$ 기능이 있다.

범주-이론적 정의

카테고리 이론의 언어에서 자유 부울 알헤브라는 세트와 함수의 범주인 세트와 부울 알헤브라와 부울 대수 동형체인 BA의 범주 사이의 연관성 측면에서 간단히 정의될 수 있다.사실, 이 접근방식은 보편적 대수학의 틀에서 정의할 수 있는 모든 대수적 구조에 일반화된다.

위에서, 우리는 자유 부울 대수는 특정한 방식으로 동작하는 발전기 세트를 가진 부울 대수라고 말했다. 또는, 한 세트에서 시작해서 그것이 어떤 대수학을 생성하는지 물어볼 수도 있다.모든 집합 X는 대수로 정의된 자유 부울 대수 FX를 생성하여 모든 대수 B와 함수 f : X → B에 대해 F를 확장하는 고유한 부울 대수 동형성 f′ : FX → B가 있다.도식적으로,

여기서 나는_X 포함이고, 파선 화살표는 독특함을 나타낸다.일단 X의 원소를 어디로 보낼지를 선택하면 부울대수동형성에 대한 법칙이 자유대수학 FX의 다른 모든 것을 어디로 보낼지를 결정한다는 생각이다.만약 FX가 X의 요소들의 조합으로 표현할 수 없는 요소들을 포함하고 있다면, F′는 독특하지 않을 것이고, X의 요소들이 충분히 독립적이지 않다면, F′는 잘 정의되지 않을 것이다!FX는 (이소모르프까지) 독특하다는 것을 쉽게 알 수 있으므로, 이 정의는 이치에 맞는다.또한 원래 정의한 대로 세트 X를 생성하는 자유 부울 대수는 FX와 이형성이므로 두 정의가 일치한다는 것을 쉽게 알 수 있다.

위의 정의 중 한 가지 단점은 도표가 f′이 동형상이라는 것을 포착하지 못한다는 것이다. 각 화살표는 단순한 함수를 나타내기 때문이다.우리는 이것을 BA와 세트 두 개의 도표로 구분하여 고칠 수 있다.두 가지를 연관시키기 위해, 우리는 functor U : BA → Set 이 대수 구조를 "잊어버리고" 알헤브라와 동형체를 그들의 기본 세트와 함수에 매핑한다.

만약 우리가 위쪽 화살표를 BA의 도표로 해석하고 아래쪽 삼각형을 Set의 도표로 해석한다면, 이 도표는 모든 함수 f : X → UB가 고유한 부울대수동형 f′ : FX → B로 확장된다는 것을 적절하게 표현한다.functor U는 f와 관련될 수 있도록 동형성 f′을 다시 세트로 끌어들이는 장치로 생각할 수 있다.

이것의 주목할 만한 측면은 후자 다이어그램이 두 개의 functor가 나란히 있을 때의 다양한 (동등) 정의 중 하나라는 점이다.우리의 F는 쉽게 functor Set → BA로 확장되며, 자유 부울 대수 FX를 생성하는 X에 대한 정의는 정확하게 U가 왼쪽 부울 F를 가지고 있다는 것이다.

위상적 실현

κ 생성기를 사용한 자유 부울 대수(여기서 κ은 유한 또는 무한의 추기경 숫자임)는 {0,1}의 개별 위상이 있다고 가정하는 제품 토폴로지를 고려할 때 {0,1}^κ의 모든 Clopen 하위 집합의 집합으로 실현될 수 있다.각 α[α]에 대해 αth 발생기는 α번째 좌표가 1인 {0,^κ1}의 모든 원소의 집합이다.특히 $\aleph _{0}$ $\aleph _{0}$ ${\$ 발생기를 $\aleph _{0}$ 가진 자유 부울대수는 칸토어 공간의 모든 클오픈 하위 집합의 집합으로, 때로는 칸토어 대수라고 불리기도 한다.이 수집품은 셀 수 있다.실제로 n개의 발전기가 유한한 자유부울대수는 카디널리티 $2^{2^{n}}$ ${\$ 을(를) 갖는 반면 $2^{2^{n}}$ 자유부울대수는 ${\$ 의 $\aleph _{0}$ $\aleph _{0}$ 모든 자유대수에 대해 c를 가진다.ardinality $\aleph _{0}$ 0 ${\$

자유 부울 대수에 대한 위상학적 접근법에 대한 자세한 내용은 부울 알헤브라에 대한 스톤의 표현 정리를 참조하십시오.

참고 항목

참조

Steve Awodey(2006) Category 이론(Oxford Logic Guiders 49).옥스퍼드 대학 출판부
Paul Halmos and Steven Givant (1998) 대수로서의 논리.미국 수학 협회
Sunders Mac Lane(1998) 작업 수학자를 위한 범주.2편 (수학 5편)스프링거-베를라크.
Sunders Mac Lane (1999년) 대수학, 3d. Ed.미국 수학 협회 ISBN 0-8218-1646-2.
로버트 R.스톨, 1963년이론과 논리 설정, 6.7장. 도버 재인쇄 1979.

Search

자유 부울 대수

네임스페이스

더

목차

간단한 예

범주-이론적 정의

위상적 실현

참고 항목

참조