F26A 그래프

F26A 그래프
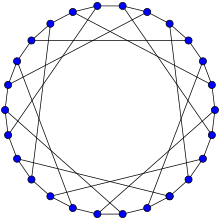F26A 그래프는 해밀턴식이다.
정점	26
가장자리	39
반지름	5
지름	5
둘레	6
자동형성	78(C13⋊C6)
색수	2
색도 지수	3
특성.	케이리 그래프 대칭 큐빅 해밀턴어[1]
그래프 및 모수 표

그래프 이론의 수학적 분야에서 F26A 그래프는 정점 26개와 가장자리 39개를 가진 대칭 쌍방향 입방 그래프다.^[1]

색도 번호 2, 색도 지수 3, 지름 5, 반지름 5, 둘레 6을 가지고 있다.^[2]또한 3-Vertex 연결, 3-edge 연결 그래프이기도 하다.

F26A 그래프는 해밀턴식이며 LCF 표기법으로 설명할 수 있다[-7, 7].¹³

대수적 특성

F26A 그래프의 자동형성 그룹은 순서 78의 그룹이다.^[3]그것은 정점, 가장자리, 그리고 그래프의 호에서 전이적으로 작용한다.따라서 F26A 그래프는 대칭 그래프(거리 전이는 아니지만)이다.그것은 어떤 정점과 어떤 가장자리로도 가져가는 자동모형을 가지고 있다.포스터 인구조사에 따르면, F26A 그래프는 26개의 정점에 대한 유일한 입방 대칭 그래프다.^[2]또한 a, ab, ab에⁴ 의해 생성된 dihedral 그룹 D에₂₆ 대한 Cayley 그래프로서,^[4] 다음과 같은 경우:

${\displaystyle D_{26}=\langle a,b a^{2}=b^{13}=1,aba=b^{-1}\angle .}$

F26A 그래프는 자동형성 그룹이 호(즉, 방향을 갖는 것으로 간주되는 가장자리)에 규칙적으로 작용하는 가장 작은 입방형 그래프다.^[5]

F26A 그래프의 특성 다항식은

${\displaystyle (x-3)(x+3)(x^{4}-5x^{2}+3)^{6}\,}$

기타 속성

F26A 그래프는 13개의 육각면을 가진 키랄 정규 지도로 토러스 안에 삽입할 수 있다.이 임베딩에 대한 이중 그래프는 순서 13의 Paley 그래프와 이형성이다.

갤러리

• 

  F26A 그래프의 색상은 2이다.

• 

  F26A 그래프의 색지수는 3이다.

• 

  F26A 그래프의 대체 도면.

• 

  Torus에 내장된 F26A 그래프.

참조