덴 트위스트

수학의 한 분야인 기하학적 위상에서 딘 트위스트는 표면의 일정한 형태의 자기 동형성이다(2차원 다지관).

정의

c가 닫히고 방향이 잡힐 수 있는 표면 S의 단순 닫힌 곡선이라고 가정하자.A를 c의 관 같은 이웃으로 두자.A는 원과 단위 간격 I:

$A\cong S^{1}\time I.}$

좌표(s, t)를 A에 부여하십시오. 여기서 s는${\displaystyle }\theta {\displaystyle }$ [${\displaystyle 0,}$ ${\displaystyle 2}$ ${\displaystyle \pi }$ ${\displaystyle ],}$ ${\displaystyle \theta \in [0,2\pi ],$ t [0, 1]과 함께 e ${\$e^{$i\ta }}}$ 형식 $복합{\displaystyle {}^{}}$ 번호로 표시하십시오.

우리가 가지고 있는 A의 외부와 내부인 S에서 그 자체로 f를 지도로 하자.

${\displaystyle f(s,t)=\왼쪽(se^{i2\pi t},t\오른쪽).}$

그 다음 f는 딘이 c 곡선을 꼬는 것이다.

딘 트위스트는 또한 방향성이 없는 표면 S에서도 정의될 수 있다. 단, S의 양면 단순 닫힘 곡선 C로 시작하는 경우.

예

가장자리 a와 b가 있는 기본 폴리곤으로 표시되는 토러스 고려

${\displaystyle \mathb {T} ^{2}\cong \mathb {R} ^{2}/\mathb {Z} ^{2}.}$

닫힌 곡선을 가장자리를 따라가는 선으로 ${\displaystyle {두십시오}_{}}$. $({\$

그림에서 동형체를 접착할 수 있는 선택으로 볼 때, 곡선의 튜브형 $근방$은 ${\$가 도넛 주위에 연결된 띠처럼 보일$$ 것이다.이 동네는 고리타분한 가정형편이라고 말한다.

${\style a(0;0,1)=\{z\in \mathb {C} :0< z <1\}}}$

복잡한 평면에서

By extending to the torus the twisting map ${\displaystyle \left(e^{i\theta },t\right)\mapsto \left(e^{i\left(\theta +2\pi t\right)},t\right)}$ of the annulus, through the homeomorphisms of the annulus to an open cylinder to the neighborhood of ${\displaystyle \gamma _$${a}$은$($는) a로 딘의 토러스 반전을 만들어 낸다.

${\displaystyle T_{a}:\mathb {T} ^{2}\to \mathb {T} ^{2}}:$

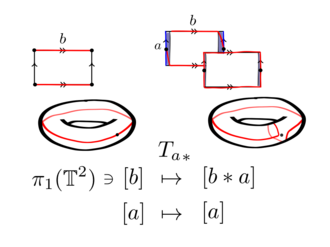
이 자기 동형성은 b를 따라 닫힌 곡선에 작용한다.관 모양의 이웃에서는 a의 곡선을 따라 b의 곡선을 한 번 취한다.

위상학적 공간 사이의 동형식은 그들의 기본 집단들 사이에 자연적인 이형성을 유도한다.그러므로 사람은 자동형성을 가지고 있다.

${\displaystyle {T_{a}_{\ast }:\pi _{1}\좌측(\mathb {T} ^{2}\우측)\pi _{1}\좌측(\mathb {T} ^{2}\우측):\x]\mapsto \왼쪽[왼쪽]T_{a}(x)\오른쪽]}$

여기서 [x]는 토러스에서 닫힌 곡선 x의 호모토피 클래스다.참고 사항 $T{\displaystyle {{}_{}}_{}}$ ${\displaystyle {a_{}}_{}}$ ${\displaystyle {{}_{}}_{}}$(${\displaystyle }$[ ${\displaystyle a}$ ${\displaystyle ]}$ )${\displaystyle }$=${\displaystyle }$[ ${\displaystyle ]}$ ${\displaystyle {T_{a}_{\ast }([a])$$=[a]}$ 및$$ T ${\displaystyle {a_{}}_{}}$ ${\displaystyle {{}_{}}_{}}$(${\displaystyle }$[ ${\displaystyle b}$ ${\displaystyle ]}$)${\displaystyle }$=${\displaystyle }$[ ${\displaystyle b}$ ${\displaystyle \ast }$ ${\displaystyle a}$ ${\displaystyle ]}$ ${\displaystyle {T_{a}_{\ast }([b])=[b*a$ 여기서 $b{\displaystyle }$ ${\displaystyle \ast }$ ${\displaystyle a}$ ${\displaystytle b*$a}은 b를 따라 이동한 경로다$$.

클래스 그룹 매핑 중

이 형태의 지도가 폐쇄적이고 지향적인 ${\displaystyle }$ 속(g {\$displaystyle g})$ 표면의$$ 동위원소 계통의 매핑 클래스 그룹을 생성하는 것은 맥스 딘의 정리다.W. B. R. R. R. R. Rickorish는 나중에 더 간단한 증거로 이 결과를 재발견했고, 또한 $Dehn$이 ${\displaystyle 3}$ ${\displaystyle \mathrm{g}}$- 1 ${\displaystyle 3g-1}$ 명시적$$ 곡선을 따라 비틀어 지도 클래스 그룹을 생성한다는 것을 보여주었다(이는 펀칭 이름 "Licorish twist organy"로 불림). 이 숫자는 나중에 Stephen P에 의해 개선되었다. 가 보여준 g> ${\displaystyle g>1$}의2$$g${\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle 2g+1}$에 대한 험프리는 최소 숫자였다

릭코리쉬는 또한 딘이 비틀리는 것뿐만 아니라 "Y-홈모피즘"을 필요로 하는 방향성이 없는 표면에도 유사한 결과를 얻었다.

참고 항목

• 연등관계

참조

• Andrew J. Casson, Steven A Bleiler, Automorism of Surfaces A Nielsen and Thurston, 1988년 캠브리지 대학 출판부. ISBN0-521-34985-0.
• 스티븐 P.험프리, "매핑 클래스 그룹의 생성기" in: 저차원 다지관의 위상(Proc) 제2회 서섹스 콘프, 첼우드 게이트, 1977), 페이지 44-47, 수학 강의 노트, 722, 스프링거, 1979년 베를린.MR0547453
• W. B. R. 릭토리쉬, "방향성 결합형 3-매니폴드의 표현." (2) 수학의 앤. 76 1962 531—540.MR0151948
• W. B. R. 릭토리쉬, "2-매니폴드의 호모토피 그룹에 대한 유한한 발전기 세트", 프로크. 케임브리지 필로스. Soc. 60 (1964), 769–778.MR0171269