축척(지도)

지도의 축척은 지도상의 거리와 지상의 해당 거리의 비율이다.이 간단한 개념은 지구 표면의 곡률에 의해 복잡해지며, 이것은 축척이 지도 전체에 걸쳐 변화하도록 강요한다.이러한 변동으로 인해 척도의 개념은 두 가지 면에서 의미가 있습니다.

첫 번째 방법은 지구 크기에 대한 지구 크기의 비율입니다.지구 생성은 지구가 축소되고 지도가 투영되는 개념적 모델이다.지구 크기에 대한 지구 크기의 비율을 공칭 척도(= 주 척도 = 대표 분수)라고 합니다.많은 지도는 공칭 척도를 나타내며 막대 척도(때로는 단순히 '척도'라고 함)를 표시할 수도 있습니다.

두 번째 뚜렷한 축척 개념은 지도 전체의 축척 변화에 적용된다.이것은 공칭 축척에 대한 매핑된 점의 축척 비율입니다.이 경우 '척도'는 척도 요인(= 점 척도 = 특정 척도)을 의미합니다.

지도의 영역이 도시 평면도와 같이 지구의 곡률을 무시할 수 있을 정도로 작으면 측정 오류를 일으키지 않고 단일 값을 척도로 사용할 수 있습니다.더 넓은 지역이나 지구 전체를 포함하는 지도에서 지도의 축척은 거리를 측정하는 데 덜 유용하거나 심지어 쓸모가 없을 수 있습니다.지도 투영법은 ^[1][2]지도 전체에서 축척이 어떻게 달라지는지를 이해하는 데 매우 중요합니다.척도가 현저하게 변동하는 경우에는 스케일 팩터로 설명할 수 있습니다.Tissot의 지표는 지도에서 점 척도의 변화를 설명하는 데 자주 사용됩니다.

역사

양적 지도 축척의 기초는 기원전 2세기에 지도 축척에 대한 개념이 이해되었다는 텍스트 증거와 함께 고대 중국으로 거슬러 올라간다.고대 중국의 측량사들과 지도 제작자들은 막대기, 목수의 정사각형, 수직선, 원을 그리기 위한 나침반, 기울기를 측정하기 위한 관측관 등의 지도를 제작하는 데 사용된 충분한 기술 자원을 가지고 있었다.고대 중국 천문학자들은 하늘을 여러 구역으로 나누거나 달 ^[3]착륙지로 구분하여 위치를 식별하는 초기 좌표계를 가정한 참조 프레임을 암시했다.

삼국시대 중국의 지도 제작자이자 지리학자 페이슈는 축척에 따라 그려진 일련의 광역 지도를 만들었습니다.그는 ^[3]지도화된 지형의 토지 측정에서 일관된 축척, 방향 측정 및 조정의 중요성을 강조하는 일련의 원칙을 제시했습니다.

용어.

규모의 표현

지도 축척은 단어(어법 척도), 비율 또는 분수로 표시할 수 있다.예를 들면 다음과 같습니다.

'1cm ~ 100m' 또는 1:10,000 또는 1/10,000

'1인치에서 1마일' 또는 1:63,360 또는 1/63,360

'1cm to 1,000km' 또는 '1:100,000,000' 또는 '1/100,000,000'입니다.(비율은 보통 1:100M으로 단축됩니다.)

막대 축척 대 어휘 축척

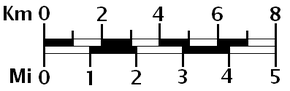
위의 지도 외에도 많은 지도에는 하나 이상의 (그래픽) 막대 축척이 있습니다.예를 들어, 몇몇 현대 영국 지도는 각각 킬로미터, 마일, 해리에 대한 세 개의 막대 눈금을 가지고 있다.

사용자에게 알려진 언어의 어휘 축척은 비율보다 시각화하기 쉬울 수 있다: 축척이 1인치에서 2마일 정도이고 지도 사용자가 지도에서 약 2인치 떨어져 있는 두 개의 마을을 볼 수 있다면, 그 마을들이 지상에서 약 4마일 떨어져 있다는 것을 알아내는 것은 쉽다.

어휘 척도가 사용자가 이해하지 못하는 언어로 표현되거나 구식 또는 잘못 정의된 단위로 표현될 경우 문제가 발생할 수 있다.예를 들어, 1인치에서 1퍼롱(1:7920)의 척도는 과거 제국주의 단위를 학교에서 가르치던 나라의 많은 노인들이 이해할 것입니다.그러나 한 리그에 대한 하나의 파우스의 축척은 지도 제작자가 리그에 사용할 수 있는 많은 정의를 선택하는 것에 따라 약 1:144,000이 될 수 있으며, 오직 소수의 현대 사용자만이 사용되는 단위를 잘 알고 있을 것이다.

대규모, 중규모, 소규모

공간 축척과 대조됩니다.

지도는 작은 축척, 큰 축척 또는 중간 축척으로 분류됩니다.스몰 스케일은 대륙이나 대국과 같은 큰 지역의 세계 지도나 지도를 말합니다.다시 말해, 그들은 좁은 공간에 넓은 면적의 땅을 보여준다.대표 분수가 상대적으로 작기 때문에 작은 척도라고 불립니다.

대규모 지도는 카운티 지도나 도시 계획 등 더 작은 지역을 더 자세히 보여줍니다.이러한 지도는 대표 분수가 상대적으로 크기 때문에 큰 축척이라고 불립니다.예를 들어 대규모 지도인 도시계획은 1:1만, 소규모 지도인 세계지도는 1:1억의 축척이 될 수 있다.

다음 표는 이러한 척도의 일반적인 범위를 설명하지만 표준이 없기 때문에 신뢰할 수 있는 것으로 간주해서는 안 된다.

분류	범위	예
대규모	1:0 – 1:600,000	바이러스 지도의 경우 1:0.00001, 시내 도보 지도의 경우 1:5000
중규모	1:600,000 – 1:2,000,000	국가 지도
소규모	1:2,000,000 – 1:∞	세계지도의 경우 1:50,000, 은하지도의 경우 1:1021

이 용어는 표의 절대적인 의미로 사용되는 경우도 있지만 상대적인 의미로 사용되는 경우도 있습니다.예를 들어, (위의 표와 같이) 대규모 지도만을 참조하는 작업을 수행하는 지도 판독기는 1:500,000의 지도를 소규모로 참조할 수 있습니다.

영어에서 large-scale이라는 단어는 종종 "확장하다"는 의미로 사용된다.그러나 위에서 설명한 바와 같이 지도 제작자들은 "대규모"라는 용어를 덜 광범위한 지도, 즉 더 작은 면적을 나타내는 지도를 가리킬 때 사용합니다.광대한 지역을 나타내는 지도는 "소규모" 지도입니다.이것은 혼란의 원인이 될 수 있습니다.

척도 변동

넓은 면적의 지도를 작성하면 지구의 곡면을 상당히 평평하게 만들기 때문에 현저한 왜곡이 발생합니다.왜곡이 분산되는 방법은 지도 투영에 따라 달라집니다.축척은 지도에 따라 다르며, 명시된 지도 축척은 근사치일 뿐입니다.이것에 대해서는, 이하에 자세하게 설명합니다.

곡률을 무시한 대규모 지도

지구가 평평하다고 간주할 수 있는 영역은 측량 측정의 정확도에 따라 달라집니다.가장 가까운 미터까지만 측정하면 약 100km(62mi)의 자오선 거리와 약 80km(위도 45도)의 동서 선에서 지구의 곡률을 감지할 수 없다.가장 가까운 1mm(0.039인치)까지 조사하면 약 10km의 자오선 거리와 약 8km의 동서 선에서 ^[4]곡률을 감지할 수 없다.따라서 1미터로 정확한 뉴욕시의 계획이나 1밀리미터로 정확한 건축 부지 계획은 곡률을 무시하기 위한 위의 조건을 모두 만족시킬 것이다.평면 측량 및 도면 상의 동일한 거리에 있는 두 점이 지면에서 동일한 거리에 있는 축척 도면으로 매핑할 수 있습니다.실제 지반거리는 지도상의 거리를 측정한 후 축척률의 역수를 곱하거나 단순히 분할기를 사용하여 지도상의 점 사이의 거리를 지도상의 막대 축척으로 이동함으로써 계산된다.

점 척도(또는 특정 척도)

가우스의 이론 이론에서 증명되었듯이, 구(또는 타원체)는 왜곡 없이 평면에 투영될 수 없다.이는 일반적으로 오렌지 껍질을 찢거나 변형시키지 않고 평평한 표면에 매끄럽게 하는 것이 불가능하다는 데서 알 수 있습니다.일정한 스케일로 구를 표현하는 유일한 참된 표현은 지구본과 같은 또 다른 구이다.

지구본의 실용적인 크기가 제한적이기 때문에, 우리는 상세한 매핑을 위해 지도를 사용해야 한다.지도에는 투영법이 필요합니다.투영에는 왜곡이 포함됩니다.지도상의 일정한 간격은 지면상의 일정한 간격에 해당하지 않는다.지도는 그래프 막대 축척을 표시할 수 있지만 지도의 일부 선에서만 정확하다는 점을 고려하여 축척을 사용해야 합니다(이 내용은 다음 섹션의 예에서 자세히 설명합니다).

P를 구(또는 타원체)의 위도$\theta {\displaystyle }$(\$displaystyle \varphi)$ 및$$ 경도$\theta {\displaystyle }$(\$displaystyle \lambda)$에 있는 점으로 합니다.Q를 인접점으로 하고 α$(\displaystyle \alpha)$를 요소 PQ와 자오선 사이의 각도로 합니다. 이 각도는 요소 PQ의 방위각입니다.P'와 Q'를 투영에서 대응하는 점으로 합니다.P'Q' 방향과 자오선 투영 사이의 각도는 $(\displaystyle \beta$입니다.$일반적$으로 α$$(\$displaystyle \alpha \neq \beta$ 주석: 지구 표면의 방위각과 지도의 정확한 구별은 거의 보편적으로 관찰되지 않습니다.바꿀 수 있게

정의: P에서의 점 척도는 Q가 P에 접근하는 한계에서의 두 거리 P'Q'와 PQ의 비율이다.우리는 이것을 다음과 같이 쓴다.

$\displaystyle \mu (\displaystyle ,\varphi ,\alpha )=\lim _{Q\to P}{\frac {P'Q'}{PQ}}}$

여기서 표기법은 점 척도가 P 위치의 함수이며 요소 PQ의 방향임을 나타냅니다.

정의: P와 Q가 동일한 자오선$({\displaystyle \alpha }$ ${\displaystyle =0}$){$displaystyle(\alpha = 0$에 있을 경우 자오선 눈금은 h${\displaystyle (}$ ${\displaystyle ,}$ ,${\displaystyle \phi }$ $){displaystyle$ h$(\displayda ,\varphi$)로 $표시$됩니다.$$

정의: P와 Q가 같은 평행$({\displaystyle \alpha }$ $=$ / 2)$${$displaystyle (\alpha$ =\$pi /2$에 있는 경우, 평행 스케일은 k${\displaystyle (}$ $)$ {$displaystyle$k(\displaystyle k$(\displayda,\varphi$로 $표시$됩니다.

정의: 점 척도가 방향이 아닌 위치에만 의존할 경우, 등방성이며 일반적으로 ${\displaystyle \mathrm{어떤}}$ 방향으로든 평행 스케일 $계수{\displaystyle }$ k${\displaystyle (}$ ${\displaystyle ,}$ , ${\displaystyle )}$)(\$displaystyle$k(\$lambda$, \$varphi$로 값을 나타냅니다.

정의:점 P에서 교차하는 모든 한 쌍의 선에 대해 점 P에서 교차하는 한 쌍의 선 사이의 각도가 투영점 P'에서 투영된 선 사이의 각도와 동일하면 지도 투영도가 적합하다고 한다.컨포멀 맵은 등방성 스케일 팩터를 가진다.반대로 지도 전체의 등방성 축척 인자는 등방성 투영을 의미한다.

규모의 등방성은 작은 요소들이 모든 방향으로 균등하게 뻗어나간다는 것을 의미하며, 그것은 작은 요소의 모양이 보존된다는 것이다.이것은 (그리스어 '오른쪽 모양'에서 유래한) 정형화의 특성이다.'작음'이라는 조건은 주어진 측정 정확도에서 요소 위의 스케일 팩터에서 변화를 감지할 수 없음을 의미합니다.등방성 투영에는 등방성 스케일 팩터가 있기 때문에 정형 투영이라고도 불립니다.예를 들어, Mercator 투영법은 각도를 보존하도록 구성되고 축척 계수가 위도만의 함수인 등방성이므로 등각 투영법입니다.메르카토르는 작은 지역에서도 모양을 유지합니다.

정의: 등방성 척도를 가진 등방성 투영에서 동일한 척도 값을 가진 점들이 등척도 선을 형성하기 위해 결합될 수 있다.최종 사용자용 지도에는 표시되지 않지만 표준 텍스트의 많은 부분이 표시되어 있습니다.(스나이더^[1] 페이지 203-206 참조).

대표분수(RF) 또는 주척도

주어진 투영식의 방정식을 설정하는 데 사용되는 두 가지 규칙이 있습니다.예를 들어, 등각 원통 투영법은 다음과 같이 쓸 수 있다.

지도 제작자: x ${\displaystyle =}$ $\displaystyle$ x$=$${\displaystyle }$$\varphi$ ${\displaystyle =}$ $\displaystyle$ y$=a\varphi }$

수학자: x ${\displaystyle =}$${\displaystyle \lambda }$ { $display style$ x = \ $varphi }$ $y$${\displaystyle }$ ${\displaystyle =}${\ { $displaystyle$ y = \ $varphi }$

여기에서는 이러한 규칙 중 첫 번째(Snyder가 실시한 조사의 사용법에 따라)를 채택한다.분명히 위의 투영 방정식은 지구를 감싸고 있는 거대한 원통 위의 위치를 정의하며, 그 다음 펼쳐집니다.이러한 좌표는 실제 인쇄된(또는 표시된) 지도와 논리적으로 구별되어야 하는 투영 지도를 정의합니다.앞의 섹션의 포인트 스케일의 정의가 투영 맵에 관한 것이라면 스케일 팩터는 통일성에 가깝다고 생각할 수 있습니다.정상 접선 원통 투영의 경우 적도를 따른 척도는 k=1이며 일반적으로 적도를 벗어나면 척도가 변합니다.투영 지도의 축척 분석은 k의 진정한 통일성 값에서 벗어난 변화를 조사하는 것입니다.

실제 인쇄된 지도는 투영 지도에서 1:100M(전체 세계 지도) 또는 1:10000(도시 계획 등)과 같은 비율로 표시된 일정한 축척으로 생성됩니다.'척도'라는 단어의 혼동을 피하기 위해 이 고정 축척 분율을 인쇄된 지도의 대표 분율(RF)이라고 하며 지도에 인쇄된 비율로 식별해야 한다.등각 원통 투영에 대해 실제 인쇄된 지도 좌표는 다음과 같습니다.

인쇄 지도: x $=$ ( ${\displaystyle R}$F $)a$ \$$lambda$$} $y$${\displaystyle }$ $=$ ( ${\displaystyle R}$F )$a$$$\ $display$ $style$ y$$= ($)$a \ $varphi }$

이 규약을 통해 고유한 투영 스케일링과 축소 스케일링을 명확하게 구분할 수 있습니다.

이 시점부터 RF를 무시하고 투영 맵을 사용합니다.

포인트 스케일 시각화: 티쏘 표시기

위도$$on { $displaystyle$\ $varphi$} 및$$ $경도{\displaystyle }$ ${\$ { $displaystyle$\ $lambda$ 지점 P를 중심으로 하는 지구 표면의 작은 원을 고려합니다. 포인트 스케일은 위치와 방향에 따라 다르므로 투영에 대한 원의 투영이 왜곡됩니다.티쏘는 왜곡이 크지 않은 한 원은 투영에서 타원이 된다는 것을 증명했다.일반적으로 타원의 치수, 모양 및 방향이 투영에 따라 변경됩니다.지도 투영에 이러한 왜곡 타원을 겹치면 지도에서 점 축척이 변경되는 방식이 전달됩니다.일그러진 타원은 티쏘의 지표로 알려져 있다.여기에 제시된 예는 미국지리학회가 만든 세계지도의 표준 투영법인 Winkel Tripel 투영법이다.최소 왜곡은 중앙 자오선에서 위도 30도(북부와 남부)입니다.(기타^[5][6] 예).

구의 일반 원통 투영을 위한 점 척도

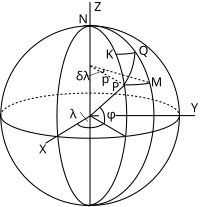
스케일을 양적으로 이해하는 열쇠는 구상의 극소수 요소를 고려하는 것이다.그림에는 구면 $위도{\displaystyle }${\(\$displaystyle \varphi)$ 및$$ $경도{\displaystyle }${\(\$displaystyle \lambda)$의 점 P가 표시되어 있습니다.포인트 Q는 $위도{\displaystyle }$+ ${\$ {\$displaydisplaydisplaydisplaydisplaydisplaydisplay$ longitude + \ $delta$$$\ $varphi$$$、경도$$ +$δdisplay$$latitude{\displaystyle }$ latitude$$$。$$PK$ 및 MQ는 ${\displaystyle 길이}$ $A$의$$경도$$ $호$입니다$.$$arphi }$은(는) 라디안 단위입니다.PM 및 KQ 라인은 길이의${\displaystyle }$평행한 ${\displaystyle \mathrm{원호}}$(${\displaystyle \cos }$ ${\displaystyle }$ ${\displaystyle )}$ ）$$ \ $displaystyle ( a$ \$cos$ \ $varphi$) \ $delta$\ $lambda$$$$}$ ( radian rad$$ )입니다.P에서 투영의 점 특성을 도출할 때 표면의 극소 원소 PMQK를 취하면 된다.P에 접근하는 Q의 한계에서는 그러한 요소는 극소 평면 직사각형에 치우치는 경향이 있다.

구의 정상적인 원통형 투영에는 ${\displaystyle x}$ ${\displaystyle a}$(\$displaystyle x=a$\displayda$$$)$$및{\displaystyle }$ y(\$displaystyle$ y$)$가 위도 함수에만 해당합니다.따라서 구면상의 극소수 원소 PMQK는 구면상의 요소를 비교하여 구면상의 요소를 비교하고 즉시 추론할 수 있으며, 이는 밑면이 ${\displaystyle \theta }$ x $= a이고 높이가$$y인$극소수 원소 P'M$'Q$$'$K$$$\text{'}$에 투영할 수 있다.평행 및 경맥의 척도 계수(일반 방향의 척도 처리는 아래에서 확인할 수 있습니다.)

$병렬$ 스케일 팩터${\displaystyle }$ k ${\displaystyle =}$ ${\displaystyle {\displaystyle \frac{\delta }{}}}$ ${\displaystyle {\displaystyle \frac{\mathrm{cosx}}{}}}$ a cos ${\displaystyle {\displaystyle \frac{、}{}}}$ ${\displaystyle {\displaystyle \frac{\mathrm{\lambda \lambda }}{}}}$ ${\displaystyle \sec }$ $=$ sec $displaydisplay$ 、 \ $dfrac {$ \ $displaystyle$\ $cos$\$varphi$、 \ $cos$ \ varphi 、 , , \ $sec$ \ varphi \ $quad$ }$=$ , \ $varphi$\ $。$

meridian 스케일${\displaystyle }$ 계수 h ${\displaystyle =}$ ${\displaystyle {\displaystyle \frac{\delta }{}}}$ ${\displaystyle {\displaystyle \frac{}{}}}$ ${\displaystyle {\displaystyle \frac{\delta }{}}}$ a $=$ y ′ （${\displaystyle {\displaystyle \frac{}{}}}$ {\ ）$$。{\$dfrac${\$displaystyle$ \displaystyle $\display y\;=\dfrac$ \$varphi$\,}$= ' dfrac {y}$

평행 스케일 $계수{\displaystyle }$ k ${\displaystyle =}$ ${\displaystyle \sec }$ ${\displaystyle }$ { $displaystyle$ k = \ $sec$\ $varphi$}는$$$$ ${\displaystyle y(}$)의 정의와 독립적이므로 모든 일반 원통 투영에서 동일합니다.주의할 필요가 있습니다.

위도 30도에서 평행 척도는 k ${\displaystyle =}$ ${\displaystyle 초{30}^{}}$ 30 ${\displaystyle {}^{}}$ ${\displaystyle 2}$/ ${\displaystyle 3\sqrt{\mathrm{}}}$ ${\displaystyle =\mathrm{}}$1.${\displaystyle 15}${\$display$ k = \$sec$ 30$^{\display$ } = 2 / {\$displayrt {$3}} =$1.15}$입니다.

위도 45도에서 평행 척도는 $k{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 초{45}^{}}$ 45 ${\displaystyle {\circ }^{}}$ ${\displaystyle {}^{}}$ $=$ 1.${\displaystyle 414}${\$displaystyle$ k =\$sec$ 45$^{\$display}$$=$secrt$ {2}}$=$ 1.$414$입니다.

위도 60도에서 평행 척도는 $k{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 초{60}^{}}$ 60 ${\displaystyle {\circ }^{}}$ $=$ { $displaystyle$ k =\$sec$ 60$^{\sec$ } =$2}$입니다.

위도 80도에서 평행 척도는 $k{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 초{80}^{}}$ 80 ${\displaystyle {\circ }^{}}$ $=$ ${displaystyle$ k=\$sec$ 80$^{\display$ } $= 5.76$입니다.

위도 85도에서 평행 척도는 k ${\displaystyle =}$ ${\displaystyle 초{85}^{}}$ 85 ${\displaystyle {\circ }^{}}$ $=$ $.$5 { $displaystyle$ k =\$sec$ 85$^{\display$ } =$11.5}$입니다.

다음 예시는 세 개의 정상적인 원통형 투영을 나타내며, 각각의 경우 티쏘의 지시표를 사용하여 위치와 방향에 따른 척도 변화를 보여 줍니다.

표준 원통 투영법의 세 가지 예

등각 투영법

플레이트 카레(프랑스어로 "평탄한 정사각형"을 의미함) 또는 등거리 투영이라고도 하는 등각 ^[1][2][4]투영법은 다음과 같이 정의됩니다.

${\displaystyle x=a\displayda,}$ ${\displaystyle y=a\varphi,}$

$여기$서$$\$displaystyle$a는$$ 구의 반지름이고$,$ \$displaystyle \displayda는$투영$$ 중심 자오선으로부터의 경도(여기서는 $= 0$에서 그리니치 자오선이라고 함)이며$,$ \$displaystyle \varphi$$$$}$는 위도입니다.${\$ { $displaystyle$\ $lambda$} 및$$$display{\displaystyle }$ { $displaystyle$\$varphi$}는$$ 라디안으로 표시됩니다(도측도에 $by{\displaystyle }${ $displaystyle \pi$ $\}$ / 180을 곱하면 알 수 있습니다).$경도{\displaystyle }$ ${\$ { ${\displaystyle \mathrm{displaystyle}}$$$\ $lambda$}는$$$$ [${\displaystyle }$- ${\displaystyle ,}$ ,$$${\displaystyle ]}$ $]$ { ${\displaystyle \mathrm{displaystyle}}$ [ - \ $pi$$$, \ $pi$$]$$、$ [ \ $displaystyle \$${\displaystyle }$$varphi$${\displaystyle }$}의${\displaystyle }$범위입니다${\displaystyle .}$

${\displaystyle y{（}^{}}$ ${\displaystyle ）}$ ${\displaystyle =}$ ${\displaystyle 1}$( \ $displaystyle$ y ' \ $varphi$ ) $=$ 1 $y{\displaystyle {}^{}}$ y$$ since $since$ 、

$병렬$ 스케일, ${\displaystyle k}$ ${\displaystyle =}$ ${\displaystyle {\displaystyle \frac{\cos }{}}}$ ${\displaystyle {\displaystyle \frac{=}{}}}$ ${\displaystyle {\displaystyle \frac{\cos }{}}}$ = ${\displaystyle {\displaystyle \frac{\sec }{}}}$ $=$ ${\displaystyle \sec }$ $displaydisplay$ 、 \ $displaystyle$\$cos$\ $varphi 、$\ $cos$ \ varphi 、 , \ $cos$ \ $varphi$ 、 , , , , \ $sec$\ $varphi$\ $qquad }$

${\displaystyle meridian}$ scale h ${\displaystyle =}$ ${\displaystyle {\displaystyle \frac{}{}}}$ y a ${\displaystyle {\displaystyle \frac{\delta }{}}}$ 1 $=$ ${\dfrac$ \displaystyle $\displaystyle h$\;=\;{$a,\dfrac$ \$varphi \,1$}

임의 방향의 점 척도 계산에 대해서는 부록을 참조하십시오.

그림은 이 투영에 대한 티쏘 표시기를 보여줍니다.적도에서 h=k=1 및 원형 요소는 투영 시에 왜곡되지 않는다.위도가 높은 곳에서는 원이 평행한 방향으로만 늘어나면 타원으로 왜곡됩니다. 자오선 방향에는 왜곡이 없습니다.장축과 단축의 비율은 sec $⁡$ { $displaystyle \sec \varphi }$이며$,$ 타원의 면적이 같은 계수만큼 커지는 것은 분명하다.

이 투영의 인쇄 버전에 나타날 수 있는 막대 축척 사용을 고려하는 것이 좋습니다.적도에서 눈금은 참(k=1)이므로 인쇄된 지도의 길이에 RF(또는 주 척도)의 역수를 곱하면 실제 지구의 둘레를 얻을 수 있습니다.지도의 막대 축척도 실제 축척으로 그려지므로 적도의 두 점 사이의 간격을 막대 축척으로 이동하면 해당 점 사이의 정확한 거리가 제공됩니다.경맥에서도 마찬가지다.적도 이외의 평행에서는 눈금이 ${\displaystyle 초}$ ${\displaystyle }${\ {\ （ \ $displaystyle \sec$ \ varphi $）$이므로 평행에서 막대 눈금으로 분리를 전환할 때 막대 스케일 거리를 이 인수로 나누어 평행선을 따라 측정했을 때 점 사이의 거리를 구해야 합니다(대원을 따라 진정한 거리가 아님).예를 들어 45도(${\displaystyle }$ ${\displaystyle =}$ ${\displaystyle {\mathrm{45도}}^{}}$ ${\$ \$displaystyle \display$=$45^{\display$의 선에서는 위도에 따라 지속적으로 변화하며, 선에 따른 분리를 바 스케일로 이동해도 실제 거리와 관련된 거리가 쉽게 주어지지 않는다(부록 참조).이 일정한 평면 각도의 선을 따라 거리를 산출할 수 있다고 해도, 투영상의 선은 구면상의 복잡한 곡선에 대응하고 있기 때문에, 그 관련성은 의문이다.이러한 이유로 소규모 지도의 막대 축척은 매우 주의해야 합니다.

메르카토르 투영법

Mercator 투영법은 방정식에^[1][2][4] 의해 구를 직사각형$(y\displaystyle$y-방향의$$ 무한 범위)에 매핑합니다.

${\displaystyle x=a\displayda}$

$(\displaystyle y=a\ln \left[\tan \leftfrac {\pi } {4} + {\frac {\varphi } {2}} \right ])$

여기서 a,$\lambda {\displaystyle }$ \ $displaystyle$\$varphi }$ $、$ display$$${\displaystyle }$ 、 \ $displaystyle$\ $varphi 、$ are$$ where 。${\displaystyle y{（}^{}}$ ${\displaystyle ）}$ ${\displaystyle =}$ $（$ \ $displaystyle$ y $（$ \ $varphi$ ） = a \ $sec$\ $varphi }$이므로 스케일 계수는 다음과 같습니다.

$병렬$ 스케일 k ${\displaystyle =}$ "${\displaystyle {\displaystyle \frac{x}{}}}$ ${\displaystyle {\displaystyle \frac{a}{}}}$ cos${\displaystyle {\displaystyle \frac{}{}}}$" " $=$ ${\displaystyle \sec }$"$$. { $displaystyle$ k \ ; = \ ; { \ $dfrac \ cos$ \$varphi$} , \ $sec \ varphi$.

meridian scale h ${\displaystyle =}$ ${\displaystyle {\displaystyle \frac{\delta }{}}}$ ${\displaystyle {\displaystyle \frac{}{}}}$ a a ${\displaystyle {\displaystyle \frac{\delta }{}}}$ a ${\displaystyle \phi }$ $=$ ${\displaystyle \sec }$ ${\displaystyle }$。{$dfrac$ { $displaystyle$ h \ ; = \$dfrac$ \ $varphi$}$$= , \$sec$ \ $varphi$. }

수학적 부록에서는 임의의 방향의 포인트 스케일이 sec${\displaystyle }$δ$$ \$displaystyle$ \$sec \varphi$와$$ ${\displaystyle \mathrm{같으므로}}$ 스케일은 등방성이며(모든 방향에서 동일), 그 크기는 sec${\displaystyle }$δ$$ \$displaystyle \sec \varphi$ $\}$ ${\displaystyle \mathrm{로서}}$ 각 무한소 요소 다이어그램에서 증가합니다.모양은 유지되지만 위도가 증가함에 따라 점점 더 커집니다.

램버트의 등면적 투영

램버트의 등면적 투영법은 방정식에^[1][2][4] 의해 구를 유한 직사각형에 매핑한다.

${\displaystyle x=a\displayda \qquad \qquad y=a\sin \varphi }$

여기서 a는 $앞$의 예시와 같습니다$.\$ $displaystyle$$\$ $varphi$are$$${\displaystyle }$$$。${\displaystyle y{（}^{}}$ ${\displaystyle ）}$ ${\displaystyle =}$ ${\displaystyle \cos }$ $（$ \ $displaystyle$ y （ \ $varphi$ ） = \ cos \ $varphi }$이므로 스케일 계수는 다음과 같습니다.

$병렬$ 스케일${\displaystyle }$ k $=$ "${\displaystyle {\displaystyle \frac{x}{}}}$ ${\displaystyle {\displaystyle \frac{a}{}}}$ cos${\displaystyle {\displaystyle \frac{}{}}}$" " " " $=$ ${\displaystyle \sec }$ "${\displaystyle }$" " " ${\displaystyle \mathrm{styledisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay}}$ " \ $displaystyle$\$cos$\ $varphi$ " , \ cos \ $cos$ \ $varphi$ " , , , \ sec \ varphi \ $qquad }$ 、 \ $sec$\ $varphi$ \ varphi \ 。

자오선 눈금 h${\displaystyle }$ ${\displaystyle =}$ = y ${\displaystyle a}$ ${\displaystyle {\displaystyle \frac{a}{}}}$ = cos ${\displaystyle =}$ cos ⁡$${ $dfrac$ \ displaystyle \$displaystyle$ \ $display$ y \ ; = { a , $\ dfrac$ \ $varphi$ } = , \$cos$ \ $varphi$}

임의의 방향의 포인트스케일 계산은 다음과 같습니다.

이제 수직 및 수평 스케일이 서로 보상하고(θ=1) 티쏘 다이어그램에서 각 극소 원형 요소는 적도의 왜곡되지 않은 원과 같은 면적의 타원으로 왜곡됩니다.

척도 요인 그래프

그래프에는 위의 세 가지 예제에 대한 척도 요인의 변동이 표시됩니다.맨 위 그림은 등방성 메르카토르 척도 함수를 보여 줍니다. 평행선의 척도는 자오선의 척도와 동일합니다.다른 그림은 등각 투영(h=1)과 램버트 등면적 투영에 대한 자오선 척도 인자를 보여준다.마지막 두 투영도는 메르카토르 그림의 투영도와 동일한 척도를 가집니다.램버트는 (메르카토르 A에 따라) 평행 척도가 위도와 함께 증가하고 (C에 따라) 자오선 척도가 위도와 함께 감소하여 면적 보존을 보장한다는 점에 주목한다.

메르카토르 투영에 대한 척도 변화

메르카토르 점 척도는 적도에서 지구와 접선을 이루도록 건설에 사용되는 보조 실린더이기 때문에 적도에서 통일됩니다.이러한 이유로 일반 투영을 접선 투영이라고 해야 합니다.척도는 위도에 ${\displaystyle \mathrm{따라}}$ k ${\displaystyle =}$ 초 $⁡$ { $displaystyle$ k = \$sec$ \ $varphi$로 변화합니다. ${\displaystyle 초}$ ${\displaystyle }$⁡ { $displaystyle \ sec$ \ $varphi$}이 ${\displaystyle 극}$에 가까워질수록 Mercator 지도는 매우 왜곡되며 이러한 이유로 (내비게이션에 대해 설명하지 않는 한) 세계 지도에 전혀 적합하지 않습니다.및 마름모꼴).단, 위도 약 25도에서는 초$(\displaystyle\sec\varphi)$의 ${\displaystyle 값}$이 약 1.1이므로 적도를 중심으로 한 50도 폭의 스트립에서는 Mercator가 10% 이내로 정확합니다.폭이 좁은 스트립이 더 좋습니다.폭 16도(적도를 중심으로)의 스트립은 100분의 1 또는 1% 이내까지 정확합니다.

적절한 대형 지도의 표준 기준은 정확도가 k $({$$displaystyle$ k$=1.0004$에 해당하는 10,000개 부분 이내(0.04%)여야 한다는 것입니다. 초$$ { $displaystyle \sec$\$varphi$ $}$은(는)$=$ 1.62 참조)에서 이 값에 도달하기$$ ${\displaystyle \mathrm{때문}}$입니다.따라서, 접선 메르카토르 투영법은 적도를 중심으로 한 폭 3.24도 내에서 매우 정확합니다.이는 남북 거리 약 360km(220mi)에 해당합니다.이 스트립 내에서는 Mercator가 적합(각도 보존)하기 때문에 매우 우수하고 정확하며 형상 보존이 가능합니다.이러한 관측은 자오선이 투영의 '적도'처럼 취급되는 횡단 메르카토르 투영법의 개발을 촉진하여 자오선에서 좁은 거리 내에 정확한 지도를 얻을 수 있도록 했다.이러한 지도는 거의 남북으로 정렬된 국가(영국 등)에 적합하며, 이러한 지도는 UTM(Universal Transverse Mercator)에 60개의 세트가 사용됩니다. 이러한 투영법(다양한 타원체에 기초함수)에서 x와 y의 변환 방정식과 축척 인자의 식은 봇의 복잡한 함수입니다.h 위도와 경도.

투영도(수정)를 나타냅니다.

2차 투영법의 기본 개념은 구체가 2개의 평행으로 교차하는 실린더에 투영되는 것입니다. $예$를 들어 § ${\displaystyle {1\mathrm{}}_{}}$(\$displaystyle \varphi$ _${1})$ 남북으로$$.이러한 위도에서 척도가 참인 반면, 이러한 위도 아래의 평행도는 투영에 의해 축소되고 (평행) 척도 계수는 1보다 작아야 한다.그 결과 위도 범위가 넓어짐에 따라 척도의 통일성 편차가 감소합니다.

예를 들어, 하나의 가능한 secant Mercator 투영법은 다음과 같이 정의됩니다.

$(\displaystyle x=0.9996a\qquad y=0.9996a\ln \left (\tan \left\frac {{pi }{4})+{\frac {varphi }{2}}\right}\)}$

숫자 승수는 투영의 모양을 변경하지 않지만 척도 요인이 수정됨을 의미합니다.

secant Mercator 척도, k${\displaystyle }$ $= 0.$ $。{$ $displaystyle$ \$sec$\ $varphi }$

따라서

• 적도의 눈금은 0.9996이다.
• ${\displaystyle {척도}_{}}$는 § 1$({$에서 k = 1입니다. ${\displaystyle \mathrm{여기}}$서 sec${\displaystyle {1\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}}$${\displaystyle 1}$ / 0${\displaystyle .9996}$ $=$ _${1$} $=$${\displaystyle {1\mathrm{}}_{}}$ /$0.9996$ $=$$1.004$$$） ${\displaystyle {}_{}}$ 1$(\displaystyle$ \$varphi)$입니다.
• k=1.0004(${\displaystyle {위도\mathrm{}}_{}}$${\displaystyle {}_{}}$ 2$({$ $\varphi _{2})$로 ${\displaystyle \mathrm{지정}}$), sec${\displaystyle 292}$ $=$ 1.${\displaystyle {0004\mathrm{}}_{}}$ / 0.9996 = 1.$0008$({$displaystyle$ \$sec \varphi _${2}$$= 1.$0004$/ ${\displaystyle 0.9996}$ $=$ 1.$0008$}({$displaystyle \varphi})$로 지정).따라서 투영은 4.58도의 넓은 스트립에 걸쳐 1< k < ${$ $displaystyle$1 <$k$ <$1.0004$}, 즉 0.04%의 정밀도를 (접선 형태의 3.24도).

이는 이전 섹션의 그림에서 아래쪽(녹색) 곡선으로 나타나 있습니다.

이렇게 좁은 고정밀 구역은 UTM 및 영국 OSGB 투영에 사용되며, 둘 다 중심 자오선 상수의 k ${\displaystyle {0\mathrm{}}_{}}$ $(\display$ style $k_{0$} $= 0.9996)$의$$눈금으로 타원체의 횡방향 Mercator이다.k ${\displaystyle =}$ {$displaystyle$ k$=1}$인 등축선은 중앙 자오선에서 동쪽과 서쪽으로 약 180km 떨어진 약간 구부러진 선입니다.스케일 팩터의 최대값은 UTM의 경우 1.001이고 OSGB의 경우 1.0007입니다.

원통형 투영 표면이 구와 교차하는 위도 § $(\$북부와 남부)의 단위 척도 선은 분할 투영의 표준 평행선입니다.

k- < . $\$ $displaystyle$k - 1 <$0$ . $0004$}의 좁은 대역은 대규모 정밀도 매핑에 중요하지만, 훨씬 넓은 간격의 표준 평행선은 축척 변동을 제어하는 데 사용됩니다.예를 들면 다음과 같습니다.

• 30N, 30S에서 표준 평행선을 갖는 베어만.
• 45N, 45S에서 표준 평행선을 가진 균등 면적.

후자의 척도 그림은 Lambert 등면적 척도 인자와 비교한 것입니다.후자의 경우 적도는 단일 표준 평행이며, 자오선 눈금의 감소를 보상하기 위해 평행 눈금이 k=1에서 증가한다.Gall의 경우, 적도에서 평행 척도가 감소(k=0.707)하는 반면, 자오선 척도는 증가(k=1.414)한다.이것은 Gall-Peters 투영법의 큰 왜곡을 일으킨다. (지구상에서 아프리카는 넓이만큼 길다.)자오선과 평행 척도는 모두 표준 평행에서 통일됩니다.

수학적 부록

일반 원통 투영에 대해, 극소 요소의 기하학적 구조는 다음을 제공합니다.

$(\displaystyle {\text{(a)}}\tan \alpha = snapfrac {a\cos \varphi\,\naph \varda}{a,\naph \varphi }})$

${\displaystyle\text{(b)}}\display\tan\tan\displays =displayfrac {a,\displays \tan}{\displays y}}.}$

$각도{\displaystyle }$$\beta$와$α$의 관계는 $다음$과 같습니다$.$

$(\displaystyle {\text{(c)}}\tan \tan \tan \tan \tan \tan \tan \tan } {a\sec \varphi }{y'(varphi)}}}\tan \alpha .,}$

Mercator 투영 y${\displaystyle {(}^{}}$ (${\displaystyle \phi }$ ) ${\displaystyle =}$ $=$ ${\displaystyle$$$\$alpha$$=\$$sec$ \$varphi$ $}$ : $각도$가 유지된다.(이는 Mercator 도출에 사용되는 관계이므로 매우 놀랍다.)등거리 투영과 램버트 투영에 $대해{\displaystyle {}^{}}$ 각각 y$$ ${\displaystyle (}$ ( ${\displaystyle )}$ ) ${\displaystyle =}$$a$ \ $displaystyle$ y' (${\displaystyle }$\ $varphi$ )$$${\displaystyle =}$ ${\displaystyle a}$ cos $⁡$$${\ \ $displaystyle$ $y$$'$ ( \ $varphi$ ) =$$a \ cos \ $varphi$} $=$ a \ $display$$$style \ valphi$$ $β$ $style{\displaystyle }$$${\ {\ {\ ${\$ {\ {\ {\ {\ {\ {\ {\ ${\displaystyle \mathrm{for}}$ for {\ {\ {\ {\ for for for$$ ${\displaystyle \mathrm{for}}$ for ${\displaystyle \mathrm{for}}$ for for ${\displaystyle \mathrm{for}}$ for$varphi$ 극소수 요소 PQ가 자오선을${\displaystyle {}_{}{\mu \alpha }_{}}$로 하여 각도α$(\$ $\$$alpha$})를$$ 만들 때 P에서의 포인트 스케일을 나타냅니다$.$ {\$displaystyle$ \$mu _${\alpha$$}}. 거리의$$ 비율로 표시됩니다.

$\displaystyle \mu _{\alpha}=\lim _{Q\to P}{PQ}=\lim _{Q\to P}{\frac {\frac x^2}+\frac y^{2}}{\frcrcrt {a^2},\var^2}phi}}\cos^{2}\varphi,\cos\cos\cosda^{2}}}.}$

식 (${\displaystyle a}$) 및 (b)에서 각각 ${\displaystyle x}$ x $=$ a (\$displaystyle \displaystyle x=a,\display$\$display$ \$display$ da$)$를 설정하고 ${\displaystyle \delta }$$$y$$(\$displaystyle \display$$$y$)$를 대입하면 다음과 같이 됩니다.

$\displaystyle \mu _{\alpha }(\varphi)=\sec \varphi \left[{\frac \sin \alpha }{\sin \sin }}\right]}$

Mercator 이외의 투영에 대해서는 먼저 방정식(c)을$$$$ 사용하여$$α와$β$(\displaystyle$\varphi$$)$로부터$β$(\$displaystyle$$\$mu_{\alpha$})$를 $계산$해야 $(\$를 $구할{\displaystyle {}_{}}$ 수 있다. 예를 들어 등각 $투영법$에는 y $=s'$가 있다$.$o 그거

$\displaystyle \tan \tan =\sec \varphi \tan \alpha .,}$

투영에서 일정한 기울기${\displaystyle }$β(\$displaystyle\beta$$)$의 직선을 고려할 때,$α(\displaystyle$\alpha$$)의 해당 값과 직선의 스케일 팩터는 모두$δ(\$displaystyle$\varphi$의 복잡한 함수이며, 일반적인 유한 분리를 바 스케일과 오타이로 전환하는 간단한 방법은 없다.의미 있는 결과를 얻을 수 있습니다.

비율 기호

콜론은 비율을 나타내는 데 자주 사용되는 반면 유니코드에서는 비율에 고유한 기호를 약간 올릴 수 있습니다.U+2236 ratio RATION(&ratio;).

「 」를 참조해 주세요.

• 지리적 거리
• 스케일(분석 도구)
• 스케일(비율)
• 스케일링(기하학)
• 공간 척도

레퍼런스