토양 통합

토양 통합은 토양이 압력의 변화에 따라 점차적으로 부피가 변하는 기계적 과정을 말한다. 이는 토양이 토양 알갱이와 모공액으로 구성된 2상 물질로 보통 지하수이기 때문에 발생한다. 물로 포화된 토양이 압력 증가를 받을 때, 토양 매트릭스에 비해 부피 강성이 높다는 것은 물이 처음에는 부피 변화 없이 압력의 모든 변화를 흡수하여 과도한 모공 수압을 발생시킨다는 것을 의미한다. 물이 스며들어 고기압의 지역에서 멀리 확산되면서 토양 행렬은 점차 압력 변화를 차지하고 부피가 축소된다. 따라서 통합의 이론적 틀은 확산방정식, 유효응력의 개념, 유압전도도와 밀접하게 관련되어 있다.

좁은 의미에서 '통합'이란 물의 점진적인 이동으로 인한 압력 변화에 대한 이러한 체적 대응을 엄격히 말한다. 일부 간행물은 넓은 의미에서 "통합"을 사용하기도 하는데, 이는 적용된 압력의 변화로 토양이 부피를 변화시키는 모든 과정을 가리킨다. 이 보다 넓은 정의는 토양 압축, 침하 및 경사의 전체적인 개념을 포함한다. 주로 유기물질이 풍부한 토양의 일부 유형은 상당한 크리프를 보이며, 물의 확산으로 인한 응집보다 오랜 시간 동안 지속되는 효과적 스트레스에 의해 토양의 부피가 서서히 변화한다. 두 메커니즘을 구분하기 위해 "1차 통합"은 과잉 수압의 소산으로 인한 통합을, "2차 통합"은 크리프 과정을 가리킨다.

해양 점토와 같이 경직성이 낮고 투과성이 낮은 토양층 위에 건물이 위치하여 수년에 걸쳐 대규모 정착으로 이어지는 경우 통합의 효과가 가장 눈에 띈다. 통폐합이 기술적 위험을 초래하는 건설사업의 종류로는 간척, 제방 건설, 점토 터널 및 지하굴착 등이 있다.

지질 공학자들은 통합의 효과를 계량화하기 위해 외측계를 사용한다. 오이디미터 테스트에서는 일련의 알려진 압력이 토양 샘플의 얇은 디스크에 적용되며, 시간에 따른 샘플 두께의 변화를 기록한다. 이를 통해 토양의 응집특성을 응집계수( $C_{v}$ $C_{v}$ ${\$ 와 유압전도율( $K$ ${\displaystyle$ K $})$ 의 관점에서 정량화할 수 있다.

역사와 용어

"토양역학의 아버지"인 Karl von Terzagi에 따르면, 통합은 "공기로 물을 대체하지 않고 포화 토양의 수분 함량을 감소시키는 과정"이라고 한다. 보다 일반적으로, 통합은 압축과 부기를 모두 포함하는 압력 변화에 대응하여 토양이 부피를 변화시키는 과정을 말한다.^[1]

볼륨 변화 규모

포화 점토에 대한 실험적으로 결정된 응집 곡선(파란색 점)은 선입체 응력 계산 절차를 보여준다.

통폐합은 장기 정하중 하중을 받는 물의 점진적인 배출이나 흡수에 의해 부피 감소가 일어나는 과정이다.^[2]

흙에 스트레스가 가해지면 흙 입자가 더 단단하게 뭉치게 된다. 이런 일이 물에 포화된 흙에서 일어나면 흙에서 물이 짜여진다. 통합의 규모는 여러 가지 방법으로 예측할 수 있다. 테르자기가 개발한 고전적인 방법에서는 토양을 외도계 시험으로 시험하여 압축성을 결정한다. 대부분의 이론적 공식에서, 로그 관계는 토양 샘플의 부피와 토양 입자가 전달하는 유효 응력 사이에서 가정된다. 비례 상수(유효응력의 크기 변화 순서에 따른 보이드 비율 변화)는 자연 로그로 계산할 때 기호 $\lambda$ $\lambda$ $\lambda$ 을(를) 부여하고 $C_{C}$ $C_{C}$ 로 $C_{C}$ 할 때 C {\displaystyle $C_{C}$ 를 부여하여 압축 지수라고 한다.^[2]^[3]

이는 토양층의 부피 변화를 추정하는 데 사용되는 다음과 같은 방정식으로 표현할 수 있다.

$\delta_{c}={\frac {C_{c}}{1+e_{0}}}H\log \left({\frac {\sigma _{zf}'}{\sigma _{z0}}}}\$

어디에

Δ는_c 연결로 인한 결제다.

C는_c 압축 지수다.

e는₀ 초기 보이드 비율이다.

H는 압축 가능한 토양의 높이다.

σ은_zf 최종 수직 응력이다.

σ은_z0 초기 수직 응력이다.

강화토양에서 스트레스가 제거되면 토양이 반등해 강화과정에서 잃었던 부피 일부를 되찾게 된다. 응력이 다시 가해지면 토양은 재압축 지수에 의해 정의된 재압축 곡선을 따라 다시 응집된다. 유효 스트레스의 로그에 대한 보이드 비율 플롯의 팽창 및 재압축 라인의 경사는 종종 "스웰링 인덱스"라고 알려진 동일한 값을 취하는데 이상적이었다(자연 로그에서 계산된 기호 $\kappa$ given ${\displaystyle \kappa },$ 베이스 10 lo에서 계산된 $C_{S}$ $C_{S}$ {\ $displaystyle C_{S}).$ 가위질하다

C는_c 최종 유효응력이 선결응력보다 적은 과잉응축토양에 사용하기 위해 C_r(재압축지수)로 대체될 수 있다. 최종 유효응력이 선입체 응력보다 클 경우, 다음과 같이 두 방정식을 조합하여 통합 프로세스의 재압축 부분과 처녀압축 부분을 모두 모델링해야 한다.

$\delta_{c}={\frac {C_{r}}{1+e_{0}}}H\log \left({\frac {\sigma _{zc}}}{\sigma _{z0}}}}\\frac {C_{1+e_{0}}}}}}})H\log \left({\frac {\sigma _{zf}}}{\sigma _{zc}}}}\$

여기서 σ은_zc 토양의 선입견적 응력이다.

이 방법은 1차원에서만 통합이 이루어진다고 가정한다. 실험실 데이터는 유효 응력 축이 로그 척도에 있는 변형률 또는 공극 비율 대 유효 응력의 그림을 구성하는 데 사용된다. 플롯의 기울기는 압축 지수 또는 압축 지수다. 보통으로 통합된 토양의 통합 정착에 대한 방정식은 다음과 같이 결정할 수 있다.

하중을 제거한 토양은 "과연 융화"된 것으로 간주된다. 이전에 빙하가 있던 토양의 경우가 그렇다. 그것이 받은 가장 높은 스트레스는 "사전 응력"이라고 불린다. "과대결합비율"(OCR)은 경험하는 최고응력을 현재응력으로 나눈 값으로 정의된다. 현재 가장 높은 스트레스를 받고 있는 토양은 "보통으로 통합된" 토양이 1의 OCR을 가지고 있다고 한다. 토양은 새로운 하중을 가한 직후에 과도한 모공 수압이 소멸되기 전에 "연결되지 않음" 또는 "연결되지 않음"으로 간주될 수 있다. 때때로, 강과 바다에서 자연 침적에 의한 토양 층층 형태는 외도계에서는 달성할 수 없는 예외적으로 낮은 밀도로 존재할 수 있다; 이 과정은 "내인적 통합"이라고 알려져 있다.^[4]

시간 의존성

봄 유추

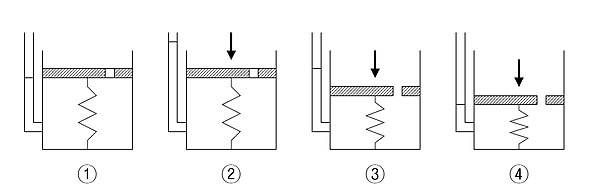
통폐합 과정은 흔히 스프링, 뚜껑에 구멍이 뚫린 용기, 물로 구성된 이상화된 시스템으로 설명된다. 이 체계에서 샘은 토양 자체의 압축성이나 구조를 나타내며, 용기에 가득 찬 물은 토양 속의 기공수를 나타낸다.

스프링 유추의 개략도

용기는 물로 완전히 채워져 있고, 구멍은 닫혀 있다.(완전 포화토양)
구멍이 아직 열리지 않은 상태에서 덮개에 하중을 가한다. 이 단계에서는 오직 물만이 가해진 하중에 저항한다.(초과공수압의 개발)
구멍을 열자마자 구멍을 통해 물이 빠지기 시작하고 스프링이 짧아진다.(과다공수압의 강우량)
얼마 후, 물의 배수는 더 이상 일어나지 않는다. 이제 스프링만으로 가해진 하중을 억제한다.(과도한 모공수압의 완전 소산. 통합 종료)

통합률 분석 공식화

통합이 일어날 시간을 예측할 수 있다. 때때로 통합에는 몇 년이 걸릴 수 있다. 이는 특히 포화상태의 클레이에서 유체 전도도가 극히 낮기 때문에, 물이 흙에서 빠져나오는 데 유난히 오랜 시간이 걸리기 때문에 더욱 그러하다. 배수가 일어나는 동안, 모공 수압은 (토양 입자와 반대되는) 작용 응력의 일부를 운반하고 있기 때문에 정상보다 크다.

$T_{v}={\frac {c_{v}*t}{(H_{dr}^{2}}\}$

여기서 T는_v 시간 요인이다.

H는_dr 통합 중 평균적으로 가장 긴 배수 경로다.

t는 측정 시간이다.

C는_v 로그 방법을 사용하여 발견된 통합 계수로 정의되며

$C_{v}={\frac {T_{50}H_{dr}^{2}}:{t_{50}}}}}}}}}}}}$

또는 다음과 같은 루트 방법

$C_{v}={\frac {T_{95}H_{dr}^{2}}:{t_{95}}}}}}}}}$

t₅₀ 시간 ~ 50% 변형(변형) 및 t는₉₅ 95%

여기서 T₉₅=1.129 T₅₀=0.197

크리프

위의 이론적 공식은 토양 단위의 시간 의존적 부피 변화만이 정상 상태의 모공 수압의 점진적 회복에 따른 효과적인 응력의 변화에만 의존한다고 가정한다. 유기물이 적은 대부분의 모래와 점토가 그렇다. 그러나 이토와 같은 유기물질이 많은 토양에서는 크리프 현상도 발생하는데, 이로 인해 토양은 일정한 유효 응력 상태에서 점차 부피가 변화한다. 토양의 크리프는 일반적으로 점성-물계의 거동과 유기물 압축에 의해 발생한다.

이 크리프의 과정은 하중의 적용에 대응하여 토양의 부피를 점진적으로 변화시키기도 하기 때문에 "2차 통합" 또는 "2차 압축"이라고도 알려져 있다; "2차 통합"이라는 명칭은 과도한 모공 수압의 소산으로 인한 부피 변화를 가리키는 "1차 통합"과 구별된다. 크리프는 일반적으로 정수압 복원 후에도 토양의 압축이 느린 속도로 이루어지도록 (1차) 통합보다 더 오랜 시간 동안 발생한다.

분석적으로 크리프 속도는 하중을 가한 후 시간이 경과함에 따라 기하급수적으로 부패하는 것으로 가정하며, 다음과 같은 공식을 제공한다.

$S_{s}={\frac {H_{0}{1+e_{0}}}C_{a}\log \left({\frac {t}{95}}\오른쪽)\}}$

여기서 H는₀ 통합 매체의 높이임
e는₀ 초기 보이드 비율이다.
C는_a 2차 압축 색인이다.
t는 통합을 고려한 후의 기간이다.
t는₉₅ 95% 통합을 달성하는 기간이다.

참고 항목

참조

^ Schofield, Andrew Noel; Wroth, Peter (1968). Critical State Soil Mechanics. McGraw-Hill. ISBN 9780641940484.
^ ^a ^b Lambe, T. William; Whitman, Robert V. (1969). Soil mechanics. Wiley. ISBN 9780471511922.
^ Chan, Deryck Y.K. (2016). Base slab heave in over-consolidated clay (MRes thesis). University of Cambridge.
^ Burland, J. B. (1990-09-01). "On the compressibility and shear strength of natural clays". Géotechnique. 40 (3): 329–378. doi:10.1680/geot.1990.40.3.329. ISSN 0016-8505.

참고 문헌 목록

Coduto, Donald (2001), Foundation Design, Prentice-Hall, ISBN 0-13-589706-8
Kim, Myung-mo (2000), Soil Mechanics (in Korean) (4 ed.), Seoul: Munundang, ISBN 89-7393-053-2
Terzaghi, Karl (1943), Theoretical soil mechanics, John Wiley&Sons, Inc., p. 265

[1] Schofield, Andrew Noel; Wroth, Peter (1968). Critical State Soil Mechanics. McGraw-Hill. ISBN 9780641940484.

[:0-2] Lambe, T. William; Whitman, Robert V. (1969). Soil mechanics. Wiley. ISBN 9780471511922.

[3] Chan, Deryck Y.K. (2016). Base slab heave in over-consolidated clay (MRes thesis). University of Cambridge.

[4] Burland, J. B. (1990-09-01). "On the compressibility and shear strength of natural clays". Géotechnique. 40 (3): 329–378. doi:10.1680/geot.1990.40.3.329. ISSN 0016-8505.

[1]

[2]

[3]

[4]

Search