학생화 범위 분포 확률밀도함수
누적분포함수
매개변수 k 1 , 그룹 수 ν {\displaystyle \nu} , 자유도 지원 q ∈ ( 0 , + ∞ ) q\in (0,+\fty )} PDF f R ( q ; k , ν ) = 2 π k ( k − 1 ) ν ν / 2 Γ ( ν / 2 ) 2 ( ν / 2 − 1 ) ∫ 0 ∞ s ν φ ( ν s ) × [ ∫ − ∞ ∞ φ ( z + q s ) φ ( z ) [ Φ ( z + q s ) − Φ ( z ) ] k − 2 d z ] d s {\displaystyle {\begin{matrix}f_{\text{R}}(q;k,\nu )={\frac {\,{\sqrt {2\pi \,}}\,k\,(k-1)\,\nu ^{\nu /2}\,}{\Gamma (\nu /2)\,2^{\left(\nu /2-1\right) }}}\int _{0}^{\infty }s^{\nu }\,\varphi ({\sqrt {\nu \,}}\,s)\,\times \\[0.5em]\left[\int _{-\infty }^{\infty }\varphi (z+q\,s)\,\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-2}\,\mathrm {d} z\right]\,\mathrm {d} s\end{matrix}}} CDF F R ( q ; k , ν ) = 2 π k ν ν / 2 Γ ( ν / 2 ) 2 ( ν / 2 − 1 ) ∫ 0 ∞ s ν − 1 φ ( ν s ) × [ ∫ − ∞ ∞ φ ( z ) [ Φ ( z + q s ) − Φ ( z ) ] k − 1 d z ] d s {\displaystyle {\display} F_{{\text{R}}(q;k,\nu )={\frac {\,{\sqrt {2\pi \,}\nu ^{\nu /2}\,}\\\\no(\nu /2)\,2^{\no /2-1\오른쪽) }}}\int _{0}^{\infty }s^{\nu -1}\,\varphi ({\sqrt {\nu \,}}\,s)\,\times \\[0.5em]\qquad \left[\int _{-\infty }^{\infty }\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-1}\,\mathrm {d} z\right]\,\mathrm {d} s\end{matrix}}}
확률 과 통계 에서 학생 범위 분포 는 정규 분포 모집단에서 학생 범위 표본 의 연속 확률 분포 다.
동일한 정규 분포 N (μ , μ 2 )을 가진 각 k 모집단 에서 n 크기의 표본을 추출하고 y 최소값 {\ displaystyle{y}_{\min}}} y 최대값 {\ displaystystyle{y}_{\max} 가장 크다고 이러한 표본으로부터의 합동 표본 분산. 그리고 다음 통계량은 학생화된 범위 분포를 가진다.
q = y ¯ 맥스. − y ¯ 분 s / n {\displaystyle q={\frac {{}}_{\max}-{\overline{y}_{\min}{s/{\sqrt{n\}}}}}}} 정의 확률밀도함수 q 에 대해 누적분포함수를 구분하면 확률밀도함수 가 나온다.
f R ( q ; k , ν ) = 2 π k ( k − 1 ) ν ν / 2 Γ ( ν / 2 ) 2 ( ν / 2 − 1 ) ∫ 0 ∞ s ν φ ( ν s ) [ ∫ − ∞ ∞ φ ( z + q s ) φ ( z ) [ Φ ( z + q s ) − Φ ( z ) ] k − 2 d z ] d s {\displaystyle f_{{\text{R}(q;k,\nu )={\frac {{\sqrt {2\pi \,}\,}\}\nu ^{\nu /2-1)\{\nu(\nu /2)\2^{\no /2-1\오른쪽) }}}\int _{0}^{\infty }s^{\nu }\,\varphi ({\sqrt {\nu \,}}\,s)\,\left[\int _{-\infty }^{\infty }\varphi (z+q\,s)\,\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-2}\,\mathrm {d} z\right]\,\mathrm {d} s} 적분 외부에서는 방정식이
φ ( ν s ) 2 π = e − ( ν s 2 / 2 ) {\displaystyle \varphi({\sqrt {\nu \,}\}\,s)\,{\sqrt {2\pi \,}}},}=e^{-\좌(\nu \,s^{2}/2\우) }} 지수 인자를 대체하기 위해 사용되었다.
누적분포함수 누적 분포 함수는 다음과 같이 지정된다.
F R ( q ; k , ν ) = 2 π k ν ν / 2 Γ ( ν / 2 ) 2 ( ν / 2 − 1 ) ∫ 0 ∞ s ν − 1 φ ( ν s ) [ ∫ − ∞ ∞ φ ( z ) [ Φ ( z + q s ) − Φ ( z ) ] k − 1 d z ] d s {\displaystyle F_{\text{R}}(q;k,\nu )={\frac {{\sqrt {2\pi \,}}\,k\,\nu ^{\nu /2}}{\,\Gamma (\nu /2)\,2^{(\nu /2-1)}\,}}\int _{0}^{\infty }s^{\nu -1}\varphi ({\sqrt {\nu \,}}\,s)\left[\int _{-\infty }^{\infty }\varphi (z)\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-1}\,\mathrm {d} z\right]\,\mathrm {d} s} 특례 k 가 2 또는 3이면 [2] 범위 where( {\displaystyle \varphi (z )} (( z ) 표준 \ )이다.
f R ( q ; k = 2 ) = 2 φ ( q / 2 ) {\displaystyle f_{R}(q;k=2)={\sqrt {2\,}\\varphi \좌측(\,q/{sqrt {2\,}}}} f R ( q ; k = 3 ) = 6 2 φ ( q / 2 ) [ Φ ( q / 6 ) − 1 2 ] {\displaystyle f_{R}(q;k=3)=6{\sqrt {2\,}\\varphi \left(\,q/{sqrt {2\,}}\오른쪽)\왼쪽[\] Phi \left(q/{\sqrt {6\,}}\오른쪽)-{\tfrac {1}{2}}\오른쪽]} 자유도가 무한대에 근접하면 표준 정규 분포를 사용하여 k에 대해 학생화된 범위 누적 분포를 계산할 수 있다.
F R ( q ; k ) = k ∫ − ∞ ∞ φ ( z ) [ Φ ( z + q ) − Φ ( z ) ] k − 1 d z = k ∫ − ∞ ∞ [ Φ ( z + q ) − Φ ( z ) ] k − 1 d Φ ( z ) {\displaystyle F_{R}(q;k)=k\,\int _{-\infty }^{\infty }\varphi (z)\,{\Bigl [}\Phi (z+q)-\Phi (z){\Bigr ]}^{k-1}\,\mathrm {d} z=k\,\int _{-\infty }^{\infty }\,{\Bigl [}\Phi (z+q)-\Phi (z){\Bigr ]}^{k-1}\,\mathrm {d} \Phi (z)} 적용들 학생화된 범위 분포의 임계값은 Tukey의 범위 테스트 에서 사용된다.[3]
학생화된 범위는 무작위로 추출하는 것이 아니라 표본 데이터의 극단적인 차이를 선택적으로 찾는 데이터 마이닝 에 의해 얻어진 결과에 대한 유의 수준을 계산하는 데 사용된다.
학생화된 범위 분포는 가설 검정 과 다중 비교 절차에 적용된다. 예를 들어, 터키의 범위 시험과 던컨의 새로운 다중 검정(첩운)은 샘플 x1,..., 수단의 xn은 표본과 q기본test-statistic은, 사후 분석으로 간에 두 그룹을 의미하 시험 하나 중요한 차이점(쌍별 비교)는 모든 그룹의 공 가설 거부하여 사용할 수 있다. f 표준 분산 분석 으로 동일한 모집단(즉, 모든 평균이 동일함)을 롬화한다.[4]
관련 분포 두 그룹 평균의 동일성(μ = μ 2 )만 문제가 되는 경우(즉, μ 1 = μ), 학생화된 범위 분포는 학생의 t 분포 와 유사하며, 첫 번째 분포가 고려 중인 평균 수를 고려한다는 점에서만 다르며, 임계 값은 그에 따라 조정된다. 고려 중인 수단이 많을수록 임계치는 커진다. 이는 평균이 많을수록 우연만으로 인해 평균 쌍 간의 차이가 최소한 유의하게 클 확률이 크기 때문에 타당하다.
파생 그 표준화된 범위 분포 함수는 표본 표준에 의해 가변 q로 편차 s로 표준화된 범위 습관적으로 표준 편차 단위에 표로 만들어져는....mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac .num,.mw-parser-output.frac .den{그 표본 범위 Rre-scaling에서 비롯된다.Font-size:80%;line-height:0;vertical-align:슈퍼}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}R⁄s. 파생은 모든 표본 데이터 분포에 적용되는 표본 범위의 분포 함수의 완전히 일반적인 형태로 시작한다.
"학생화" 범위 q 의 관점에서 분포를 얻기 위해 R 에서 s 와 q 로 변수를 변경한다. 표본 데이터가 정규 분포 를 따른다고 가정할 때 표준 편차 χ 분포 가 된다. s 를 더 통합함으로써 우리는 매개변수 로서 s를 제거하고 q 의 측면에서만 재확대된 분포를 얻을 수 있다.
일반형식 확률밀도함수 f 에X f 는R [2]
f R ( r ; k ) = k ( k − 1 ) ∫ − ∞ ∞ f X ( t + 1 2 r ) f X ( t − 1 2 r ) [ ∫ t − 1 2 r t + 1 2 r f X ( x ) d x ] k − 2 d t {\displaystyle f_{R}(r;k)=k\,(k-1)\int _{-\infty }^{\infty }f_{X}\left(t+{\tfrac {1}{2}}r\right)f_{X}\left(t-{\tfrac {1}{2}}r\right)\left[\int _{t-{\tfrac {1}{2}}r}^{t+{\tfrac {1}{2}}r}f_{X}(x)\,\mathrm {d} x\right]^{k-2}\,\mathrm {d} \,t} 즉, 분포에서 k 를 끌어와 그 중 2가 r 로 차이를 보이고, 나머지 k - 2가 모두 두 극단값 사이에 속할 확률을 더하는 것이다. 변수 u 1 2 r {\displaystyle u=t-{\tfrac {1}{2}}r} F 를X f 의X
f R ( r ; k ) = k ( k − 1 ) ∫ − ∞ ∞ f X ( u + r ) f X ( u ) [ F X ( u + r ) − F X ( u ) ] k − 2 d u {\displaystyle f_{R}(r;k)=k\,(k-1)\int _{-\infty }^{\infty }f_{X}(u+r)\,f_{X}(u)\,\left[\,F_{X}(u+r)-F_{X}(u)\,\right]^{k-2}\,\mathrm {d} \,u} 유사한 통합형 제품을 소개하며, 통합형 신호에 따라 차별화하면
∂ ∂ r [ k ∫ − ∞ ∞ f X ( u ) [ F X ( u + r ) − F X ( u ) ] k − 1 d u ] = k ( k − 1 ) ∫ − ∞ ∞ f X ( u + r ) f X ( u ) [ F X ( u + r ) − F X ( u ) ] k − 2 d u {\displaystyle {\begin{aligned}{\frac {\partial }{\partial r}}&\left[k\,\int _{-\infty }^{\infty }f_{X}(u)\,{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,u\right]\ \[5pt]={}&k\,(k-1)\int _{-\infty }^{\infty }f_{X}(u+r)\,f_{X}(u)\,{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-2}\,\mathrm {d} \,u\end{aligned}}} 위와 같은 핵심을 회복해서 [a]
F R ( r ; k ) = k ∫ − ∞ ∞ f X ( u ) [ F X ( u + r ) − F X ( u ) ] k − 1 d u = k ∫ − ∞ ∞ [ F X ( u + r ) − F X ( u ) ] k − 1 d F X ( u ) {\displaystyle {\reasoned} F_{R}(r;k)&=k\int _{-\infty }^{\infty }f_{X}(u){\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,u\\&=k\int _{-\infty }^{\infty }{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,F_{X}(u)\end{aligned}}} 왜냐하면 어떤 연속적인 cdf 에 대해서도
∂ F R ( r ; k ) ∂ r = f R ( r ; k ) {\displaystyle {\frac {\partial F_{R}(r;k)}{\partial r}=f_{R}(r;k)} 정규 데이터에 대한 특수 양식 범위 분포는 표본 평균 주위의 신뢰 구간에 가장 자주 사용되며, 이는 중앙 한계 정리 에 의해 점증적으로 정규 분포 를 따른다.
정규 데이터에 대한 학생화 범위 분포를 생성하기 위해 먼저 일반 f 와X F 에서X 표준 정규 분포 에 대한 분포 함수 φ 과 φ로 전환하고 변수 r 을 s/q 로 변경하며, 여기서 q 는 스케일링 계수 s 에 의해 r을 재스케일화하는 고정 인자:
f R ( q ; k ) = s k ( k − 1 ) ∫ − ∞ ∞ φ ( u + s q ) φ ( u ) [ Φ ( u + s q ) − Φ ( u ) ] k − 2 d u {\displaystyle f_{R}(q;k)=s\,k\,(k-1)\int _{-\infty }^{\infty }\varphi (u+sq)\varphi (u)\,\left[\,\Phi (u+sq)-\Phi (u)\right]^{k-2}\,\mathrm {d} u} q가 범위가 넓은 표준 편차의 수가 되도록 스케일링 계수 s 를 표본 표준 편차로 선택한다. 정규 데이터의 경우 s 는 ki 분산 이고[b] ki 분포의 분포 함수 S
f S ( s ; ν ) d s = { ν ν / 2 s ν − 1 e − ν s 2 / 2 2 ( ν / 2 − 1 ) Γ ( ν / 2 ) d s 을 위해 0 < s < ∞ , 0 그렇지 않으면 . {\displaystyle f_{S}(s;\nu )\,\mathrm {d} s={\begin{cases}{\dfrac {\nu ^{\nu /2}\,s^{\nu -1}e^{-\nu \,s^{2}/2}\,}{2^{\left(\nu /2-1\right)}\Gamma (\nu /2)}}\,\mathrm {d} s&{\text{for }}\,0<s<\infty ,\\[4pt]0&{\text{otherwise}}. \end{case}}} 분포R S f 를 곱하고 표준 편차 s에 대한 의존성을 제거하기 위해 통합하면 정규 데이터에 대한 학생화된 범위 분포 함수를 얻을 수 있다.
f R ( q ; k , ν ) = ν ν / 2 k ( k − 1 ) 2 ( ν / 2 − 1 ) Γ ( ν / 2 ) ∫ 0 ∞ s ν e − ν s 2 / 2 ∫ − ∞ ∞ φ ( u + s q ) φ ( u ) [ Φ ( u + s q ) − Φ ( u ) ] k − 2 d u d s {\displaystyle f_{R}(q;k,\nu )={\frac {\nu ^{\nu /2}\,k\,(k-1)}{2^{\left(\nu /2-1\right)}\Gamma (\nu /2)}}\int _{0}^{\infty }s^{\nu }e^{-\nu s^{2}/2}\int _{-\infty }^{\infty }\varphi (u+sq)\,\varphi (u)\,\left[\,\Phi (u+sq)-\Phi (u)\right]^{k-2}\,\mathrm {d} u\,\mathrm {d} s} 어디에
q 는 표준 편차로 측정한 데이터 범위의 폭이다.ν [c] k 는 범위 내에서 점을 구성하는 개별 평균 수입니다.위의 섹션에 나와 있는 pdf 에 대한 방정식은 사용에서 비롯된다.
e − ν s 2 / 2 = 2 π φ ( ν s ) {\displaystyle e^{-\nu \,s^{2}/2}={\sqrt {2\pi \,}\varphi({\sqrt {\nu \,}\s)} 외부 적분에서 지수 식을 대체한다.
메모들 ^ 기술적으로, 그 관계는 다음 섹션에서 논의한 대로 정상 데이터에 대해 모든 곳에 있는 f X u r 0 {\displaystyle f_{X}(u+r)>0 u {\displaystyle u} 균일하게 분포 된 데이터와 같이 지원 범위가 상한 분포에는 해당되지 않는다. ^ "제곱"이 없다는 점에 유의하십시오. 본문은 χ 2 분포아니라 χ 분포 를 가리킨다. ^ 일반적으로 ν n 1 {\displaystyle \nu =n-1 n 은 범위의 값인 평균을 찾는 데 사용되는 모든 기준점의 총 수입니다. 참조 ^ Lund, R.E.; Lund, J.R. (1983). "Algorithm AS 190: Probabilities and upper quantiles for the studentized range". Journal of the Royal Statistical Society . 32 (2): 204–210. JSTOR 2347300 . ^ a b McKay, A.T. (1933). "A note on the distribution of range in samples of n ". Biometrika 25 (3): 415–420. doi :10.2307/2332292 . JSTOR 2332292 . ^ [1] ^ Pearson & Hartley(1970, 섹션 14.2)
추가 읽기 외부 링크 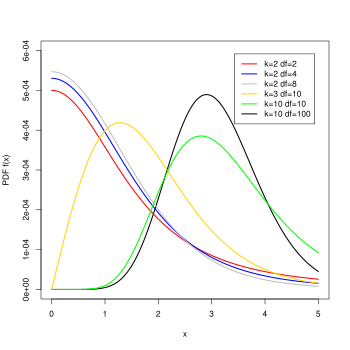



![{\displaystyle {\begin{matrix}f_{\text{R}}(q;k,\nu )={\frac {\,{\sqrt {2\pi \,}}\,k\,(k-1)\,\nu ^{\nu /2}\,}{\Gamma (\nu /2)\,2^{\left(\nu /2-1\right)}}}\int _{0}^{\infty }s^{\nu }\,\varphi ({\sqrt {\nu \,}}\,s)\,\times \\[0.5em]\left[\int _{-\infty }^{\infty }\varphi (z+q\,s)\,\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-2}\,\mathrm {d} z\right]\,\mathrm {d} s\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a08d81086431dd9b1ebae17991b17d2ee4642b6)
![{\displaystyle {\begin{matrix}F_{\text{R}}(q;k,\nu )={\frac {\,{\sqrt {2\pi \,}}\,k\,\nu ^{\nu /2}\,}{\,\Gamma (\nu /2)\,2^{\left(\nu /2-1\right)}}}\int _{0}^{\infty }s^{\nu -1}\,\varphi ({\sqrt {\nu \,}}\,s)\,\times \\[0.5em]\qquad \left[\int _{-\infty }^{\infty }\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-1}\,\mathrm {d} z\right]\,\mathrm {d} s\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b83772014edd9847eab4060054dce9407acffaf2)
 (가) 이러한 표본 평균 중 가장 작으며
(가) 이러한 표본 평균 중 가장 작으며 

![{\displaystyle f_{\text{R}}(q;k,\nu )={\frac {{\sqrt {2\pi \,}}\,k\,(k-1)\,\nu ^{\nu /2}}{\Gamma (\nu /2)\,2^{\left(\nu /2-1\right)}}}\int _{0}^{\infty }s^{\nu }\,\varphi ({\sqrt {\nu \,}}\,s)\,\left[\int _{-\infty }^{\infty }\varphi (z+q\,s)\,\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-2}\,\mathrm {d} z\right]\,\mathrm {d} s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20b454e7c3be46bad6a6b685406779af6e53aad8)

![{\displaystyle F_{\text{R}}(q;k,\nu )={\frac {{\sqrt {2\pi \,}}\,k\,\nu ^{\nu /2}}{\,\Gamma (\nu /2)\,2^{(\nu /2-1)}\,}}\int _{0}^{\infty }s^{\nu -1}\varphi ({\sqrt {\nu \,}}\,s)\left[\int _{-\infty }^{\infty }\varphi (z)\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-1}\,\mathrm {d} z\right]\,\mathrm {d} s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c21803c454533585edeaa35d2b23061da152de3f)
 표준 정규 확률밀도함수이고
표준 정규 확률밀도함수이고 

![{\displaystyle f_{R}(q;k=3)=6{\sqrt {2\,}}\,\varphi \left(\,q/{\sqrt {2\,}}\right)\left[\Phi \left(q/{\sqrt {6\,}}\right)-{\tfrac {1}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492f3d60fda45450ff9e9a619b855bb61fb1f5f1)
![{\displaystyle F_{R}(q;k)=k\,\int _{-\infty }^{\infty }\varphi (z)\,{\Bigl [}\Phi (z+q)-\Phi (z){\Bigr ]}^{k-1}\,\mathrm {d} z=k\,\int _{-\infty }^{\infty }\,{\Bigl [}\Phi (z+q)-\Phi (z){\Bigr ]}^{k-1}\,\mathrm {d} \Phi (z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f380dc1c42ad0123fbaf0159324121161c99fec0)
![{\displaystyle f_{R}(r;k)=k\,(k-1)\int _{-\infty }^{\infty }f_{X}\left(t+{\tfrac {1}{2}}r\right)f_{X}\left(t-{\tfrac {1}{2}}r\right)\left[\int _{t-{\tfrac {1}{2}}r}^{t+{\tfrac {1}{2}}r}f_{X}(x)\,\mathrm {d} x\right]^{k-2}\,\mathrm {d} \,t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/462ed05fb46aaf8cae430562c3f64d5c1e0d06a7)

![{\displaystyle f_{R}(r;k)=k\,(k-1)\int _{-\infty }^{\infty }f_{X}(u+r)\,f_{X}(u)\,\left[\,F_{X}(u+r)-F_{X}(u)\,\right]^{k-2}\,\mathrm {d} \,u}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f87b66f2887c8ba73d449fe77097473b9bffeb25)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial r}}&\left[k\,\int _{-\infty }^{\infty }f_{X}(u)\,{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,u\right]\\[5pt]={}&k\,(k-1)\int _{-\infty }^{\infty }f_{X}(u+r)\,f_{X}(u)\,{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-2}\,\mathrm {d} \,u\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79ce11373630f6a4a3d2e1d4b738219af75b9388)
![{\displaystyle {\begin{aligned}F_{R}(r;k)&=k\int _{-\infty }^{\infty }f_{X}(u){\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,u\\&=k\int _{-\infty }^{\infty }{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,F_{X}(u)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5194b7fd58dd44d6e6c4929e2f2e6387e481c29)

![{\displaystyle f_{R}(q;k)=s\,k\,(k-1)\int _{-\infty }^{\infty }\varphi (u+sq)\varphi (u)\,\left[\,\Phi (u+sq)-\Phi (u)\right]^{k-2}\,\mathrm {d} u}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f9533dfe9031ad819e3339f0d818cdf94cd4655)
![{\displaystyle f_{S}(s;\nu )\,\mathrm {d} s={\begin{cases}{\dfrac {\nu ^{\nu /2}\,s^{\nu -1}e^{-\nu \,s^{2}/2}\,}{2^{\left(\nu /2-1\right)}\Gamma (\nu /2)}}\,\mathrm {d} s&{\text{for }}\,0<s<\infty ,\\[4pt]0&{\text{otherwise}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc1a8ce22925692c9ab3ea76b180775656bcd99e)
![{\displaystyle f_{R}(q;k,\nu )={\frac {\nu ^{\nu /2}\,k\,(k-1)}{2^{\left(\nu /2-1\right)}\Gamma (\nu /2)}}\int _{0}^{\infty }s^{\nu }e^{-\nu s^{2}/2}\int _{-\infty }^{\infty }\varphi (u+sq)\,\varphi (u)\,\left[\,\Phi (u+sq)-\Phi (u)\right]^{k-2}\,\mathrm {d} u\,\mathrm {d} s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13c262ebcd5ba753289f769a9460f66ab945c75d)


 지점
지점 


