스큐 격자
Skew lattice추상 대수학에서 꼬치 격자는 격자의 비확정 일반화인 대수적 구조다.스큐 격자란 용어는 격자의 비확정 일반화를 가리키는 데 사용될 수 있지만, 1989년부터는 주로 다음과 같이 사용되어 왔다.
정의
스큐 래티스(skew lattice)는 다음과 같은 이중 흡수 법칙 쌍을 검증하는 두 개의 연관성, 공회전 이진 연산 및 이(가) 장착된 세트 S이다.
과와) {\ \wedge 이(가) 연관성이 있고 idempotent임을 감안할 때, 이러한 ID는 다음과 같은 이중 쌍의 진술을 검증하는 것과 같다.
역사적 배경
60년 이상 동안, 다른 동기를 가지고 격자의 비확실성 변형이 연구되어 왔다.어떤 사람들에게는 그 동기가 격자 이론의 개념적 경계에 대한 관심이었고, 다른 사람들에게는 논리와 부울 대수의 비확정적 형태에 대한 탐색이었다. 그리고 다른 사람들에게는 고리 안의 특이점들의 행동이었다.일반적으로 말해서 비확장 격자(noncommative lattice)는 대수; , ) {\과이(가) 어떤 식으로든 }을 보장하는 흡수 정체성에 의해 연결된 연관적이고 특이한 이진 연산이다. 선택한 정확한 정체성은 근본적인 동기에 따라 달라지며, 다른 선택이 뚜렷한 알헤브라를 생산한다.
Pascual Jordan은 양자논리에 관한 질문에 동기부여를 받아 1949년 논문인 Uber Nichtkommutative Bubénde에서 흡수 정체성을 선택하면서 [2]비확정적 격자 연구를 시작했다.
그는 그들을 만족시키는 알헤브라를 슈레그베르벤데라고 불렀다.이러한 정체성을 변화시키거나 증가시킴으로써, 조던과 다른 사람들은 많은 종류의 비협정 격자를 얻었다.조나단 리흐의 1989년 논문인 링의 스큐 래치,[3] 위에서 정의한 스큐 래치 등을 시작으로 지금까지 주요 연구 대상이 되어 왔다.이것은 밴드에 대한 이전의 결과에 의해 도움을 받았다.이것은 특히 많은 기본 재산의 경우였다.
기본 속성
자연적 부분순서와 자연 퀘이서더
In a skew lattice , the natural partial order is defined by if , or dually, . 의 자연적 사전 은 y x= = y x\ 또는 dolly ∨ { = 에 의해 주어진다 과와) 이(가) 선반에는 동의하지만, }은(는) 비전속 사례에서 적절하게 조정된다.The induced natural equivalence is defined by if , that is, and or dually, 및 x = 의 블록은 A 및 이 > 과 같이 존재하는 경우 > 가 주문하는 격자다.이를 통해 다음 쌍과 같은 스큐 래치 하세 다이어그램을 그릴 수 있다.
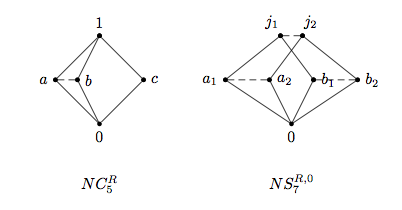
를 들어, 위 왼쪽에 있는 다이어그램에서 b{\이(가) 과(와) 관련되어 있음을 점선 세그먼트로 표현한다.기울어진 선은 구별되는 -classes의 요소들 사이의 자연스러운 부분 순서를 보여준다.요소 1 및 은(는) 싱글톤 -classes를 형성한다.
직사각형 스큐 래티스
단일 클래스로 구성된 스큐 래치를 직사각형이라고 한다.They are characterized by the equivalent identities: , and . Rectangular skew lattices are isomorphic to skew lattices having the following construction (and conversely): given nonempty sets and , on define and . The -class partition of a skew lattice {\은(는) 위 다이어그램에 표시된 최대 직사각형 하위 골격에 대한 S S의 고유한 파티션이며, 더욱이 은 유도 지수 대수 }이(가) {의 최대 래티스 이미지와 일치한다.따라서 모든 꼬치 격자 S을 직사각형 하위 격자 격자로 만든다.이것은 꼬치 격자에 대한 클리포드-맥클린 정리인데, 클리포드와 맥클린에 의해 처음으로 밴드에 대해 별도로 주어진다.스큐 래치에 대한 최초의 분해 정리라고도 한다.
오른쪽(왼쪽) 손 스큐 격자 및 키무라 인수
꼬치 격자는 ID x y = ∧ = y x ∧ x{ x { x { x \ x x 또는 x y x = x { y ∨ y { y{ x { { x { x = = x = x = x = x = x = x = x = x = x = = x = x = x = x = x = x 정체성은 및 = 을(를) 각 D {\ -class에서 기본적으로 주장하고 있다.Every skew lattice has a unique maximal right-handed image where the congruence is defined by if both and (or dually, 및 = y x로 각 -class에서 y= x x y 및 = 인 경우 꼬치 격자도 왼손잡이임.다시 한 번 스큐 S {\S}의 최대 왼손 이미지는 R{\ S 이미지인데, 서스큐 격자 R {\ R}은 L 에 대해 이중 방식으로 정의된다 스큐 격자의 많은 예는 오른손 또는 왼손이다.In the lattice of congruences, and is the identity congruence . The induced epimorphism factors through both induced epimorphisms 및 → / R T= / 동형상 : → S/ / ( )=( , )에 의해 된 SS/S/ 에 의해 정의된 S\rightarrow :S/ 을(를) 최대 오른손과 왼손 이미지의 섬유화된 제품으로 인수한 키무라 요인화다.

Clifford-McLan 정리처럼, 키무라 인수화(또는 스큐 래티스의 두 번째 분해 정리)는 정규 밴드( 흡수 아이덴티티를 만족하는 밴드, x = x x x x x x x x x x 에 대해 먼저 주어졌다.실제로 과 은(는) 모두 일반 밴드 작업이다.위의 기호 및 은 물론 기본 세미그룹 이론에서 온다.[3][4][5][6][7][8][9][10]
스큐 래티 하위 변수
꼬치 격자는 다양하다.직사각형 꼬치 격자, 왼손 및 오른손 꼬치 격자는 모두 꼬치 격자의 기본 구조 이론의 중심인 하위 분리를 형성한다.여기 몇 개가 더 있다.
대칭 스큐 래티스
A skew lattice S is symmetric if for any , if . Occurrences of commutation are thus unambiguous for such skew lattices, with subsets of pairwise commuting elements generating commutative subalgebr예를 들어 하위 항목으로(일반적으로 꼬치형 선반에는 해당되지 않는다.)이 아변종에Equational 기지, 먼저 Spinks[11]에 의해:)∨ y∨()∧ y)=(y∧))∨ y∨){\displaystyle x\vee y\vee(이x\wedge)=(y\wedge))\vee y\vee)}, 탭 ∧ y∧()∨ y)=(y∨))∧ y∧){\displaystyle x\wedge(x\vee y)=(y\vee))\wedge y\wedge y\wedge)}. 비스듬한 S격자{\displa의 격자 부분이다.yst은(는) 요소에서 각 D {\ D -class S {\ 을를) S {\ S의 하위 다. T 은 격자 {\ S의 내부 복사본이며, → 는 이형성이다.S/D \leq \aleph_0에 대한 모든 대칭 스큐 래티스는 격자 섹션을 허용한다.[10]Symmetric or not, having a lattice section guarantees that also has internal copies of and given respectively by and , where and are the and congruence classes of in . Thus 과 [ → S / S은 이형성이다.[8]이는 앞의 기무라 도표를 이원화하는 것을 내장한 통근 도표로 이어진다.

취소식 스큐 래티스
A skew lattice is cancellative if and implies and likewise and implies 취소 스큐 격자는 대칭이며 다양성을 형성하는 것으로 보여질 수 있다.선반과 달리, 그것들은 분배될 필요가 없으며, 반대로도 필요하다.
분배 스큐 격자
분배 스큐 격자는 다음과 같은 정체성에 의해 결정된다.
( z) x=( x x) ( z ) { (x ∧ ∧ x ) z)\wedge x=(x ()
(D'1)
(D1)과 (D'1)는 격자와 달리 일반적으로 스큐 격자의 경우 등가물이 아니지만 대칭적 스큐 격자의 경우 등가물이 된다.[9][12][13]조건(D1)은 다음과 같이 강화될 수 있다.
z) w=( x w) ( ) ∨ (x ∧ z ∧ w ) (x ∧ z ∧ w ) {\ z wD2)
이 경우(D'1)는 결과물이다.A skew lattice satisfies both (D2) and its dual, , if and only if it factors as the product of a distributive lattice and a rectangular skew lattice.이 후자의 경우(D2)는 다음과 같이 강화될 수 있다.
and . (D3)
그 자체로 (D3)는 대칭이 추가되었을 때 (D2)와 동등하다.[3]따라서 (D1), (D2), (D3) 및 그 이중으로 각각 결정된 6개의 스큐 격자 하위 분리가 있다.
일반 스큐 래티스
위에서 보듯이∧ 과 은(는) x x x x x x x x x xx x x x 을(는 만족하는 밴드를 정상이라고 한다스큐 격자는 만족하는 경우 일반적인 스큐입니다.
For each element a in a normal skew lattice , the set defined by {} or equivalently {} is a sublattice of , and conversely. (따라서 정상적인 스큐 래티들은 로컬 래티라고도 불린다.) 과both \이(가) 모두 정상일 때 S {\ S}은 격자 및 직사각형 스큐 D D의 제품 및 반대로 D과(으)로 이형 분할된다.따라서 일반 스큐 격자와 스플릿 스큐 격자 모두 품종을 형성한다.분포로 돌아가기 (2)= ( )+ ( ) 을(를)}하여( 2){\은 분포의 다양성, 정규 스큐 격자, 정규 스큐 격자 등의 특성을 나타낸다.
범주형 스큐 래티스
꼬치 격자는 코제트 반대편의 비어 있지 않은 합성물이 코제트 반대인 경우 범주형이다.범주형 스큐 격자는 다양성을 형성한다.링의 꼬치 격자와 일반 꼬치 격자는 이 품종의 알헤브라의 예다.[4]A{A\displaystyle}B{B\displaystyle}에서 b>C{\displaystylec\in C}∈ ∈과 요리{\displaystyle a>, b>, 요리}A{\displaystyle a\in}, b∈ B{\displaystyle b\in B}과 c를 사용하자, φ{\displaystyle \varphi}이 되coset bijection에 대한 largeenough{\di{\displaystyle}를 복용하고 있다.splaystyle, be the coset bijection from to taking to and finally be the coset bijection from to taking to . A skew lattice is categorical if one always has the equality , i.e. , if the composite partial bijection if nonempty is a coset bijection from a -coset of to an -coset of . That is 모든 분배 스큐 래티들은 범주형이다.대칭 스큐 격자는 아닐 수 있지만.어떤 의미에서 그들은 대칭성과 분배성 사이의 독립성을 드러낸다.[3][4][6][9][10][11][13][14]
스큐 부울 알헤브라스
A zero element in a skew lattice S is an element 0 of S such that for all or, dually, (0)
A Boolean skew lattice is a symmetric, distributive normal skew lattice with 0, such that is a Boolean lattice for each Given such skew lattice S, a difference operator \ is defined by x \ y =- x y 서 후자는 부울 격자 x 0 x . (D3) 및 (0)가 있는 경우[1] \은 다음과 같은 정체성을 특징으로 한다.
and S B)
그러므로 하나는 정체성 (D3)과 (0) 그리고 (S B)로 특징지어지는 다양한 꼬치 부울 알헤브라스 ; , , ) 을 가지고 있다.원시 스큐 부울 대수는 0과 단일 비 0 D 등급으로 구성된다.따라서 이는 (0)을 통해 직사각형 꼬치 격자 D에 ∖ = x = x x y을를) 연결한 결과(= = 0 = 및 0{\모든 꼬치 부울 대수는 원시 알헤브라의 하위직 산물이다.스큐 부울 알헤브라는 부울행동의 보편적 대수학에서 판별자 품종과 기타 일반화를 연구하는 데 중요한 역할을 한다.[15][16][17][18][19][20][21][22][23][24][25]
링의 스큐 래치
Let be a ring and let denote the set of all idempotents in . For all set and .
분명히 은(는 연관성이 있다 집합 E( ) 이(가) }, ( ,,)에 따라 닫힌 경우, 취소형 스큐 래티스인 것이다( ) 에서 이러한 꼬치 격자를 찾으려면 ( A 의 밴드를 살펴보는데 특히 어떤 제약조건에 관해서 최대치인 밴드를 살펴본다.실제로 올바른 정규(= )에 관해서 최대인 () 의 모든 승수 대역도 에 따라 닫히므로 오른손 스큐 격자를 형성한다.In general, every right regular band in generates a right-handed skew lattice in . Dual remarks also hold for left regular bands (bands satisfying the identity ) in . Maximal regular bands need not정의된 대로as 에 따라 닫으십시오. counterexamp는 승법 직사각형 밴드를 사용하여 쉽게 찾을 수 있다.These cases are closed, however, under the cubic variant of defined by since in these cases reduces to to give the dual rectangular band.By replacing the condition of regularity by normality , every maximal normal multiplicative band in is also closed under with 여기서 / y= - x x 는 부울 스큐 격자를 형성한다.( ) 자체가 곱셈으로 닫히면 정상 대역이므로 부울 스큐 격자를 형성한다.사실, 어떤 꼬불꼬불한 대수학도 그러한 대수학 속에 삽입될 수 있다.[26]A가 승수적 정체성 을 갖는 경우, ( 이 승수적으로 닫힌다는 조건은E () 이 부울대수를 형성한다는 것을 암시하는 것으로 잘 알려져 있다.고리 안의 꼬치 격자는 계속해서 좋은 예와 동기 부여의 원천이 된다.[23][27][28][29][30]
원시 스큐 격자
정확히 두 개의 D등급으로 구성된 꼬치 격자를 원시 꼬치 격자라 한다. S}의 A> > B 와 꼬치 격자 이(가 있을 경우, a\ B이가 하위된다.
{} and {}
각각 B에서는 A의 코세츠, A에서는 B의 코세츠라고 불린다. ∧ ∧ ∧ { { { { { { { {{ { { wed wed a wed wed a a wed partition partition partition wed partition partition partition partition partition partition partition partition partition partition partition partition partition partition partition partition wed wed partition wed wed wed wed wed partition wed partition partition partition 더욱이 부분 순서 은(는) 코제트 바이어스 : B a → 에 의해 정의된다.
( )= ( ifff x> y 에 대한 x B B y A A
코제트 편차는 집합적으로 하위 집합 A과 사이의between 을(를) 설명한다또한 구별되는 -classes의 요소 쌍에 대해for 및 을(를) 결정한다.Indeed, given and , let be the cost bijection between the cosets in and in . Then:
and .
일반적으로 을을 가진{\displaystyle a,c\in}과 b, d∈ B{\displaystyle b,d\in B};b{\displaystyle a>, b}과 c>d{\displaystyle c>, d}, 그 흔한 B{B\displaystyle}-잉여류에 대한{A\displaystyle}, b, d{\displaysty에 c{\displaystyle a,c}에 속하∈, c.b,d} 르> // > 의 AA -coset까지 길게 .따라서 각 코셋 편향은 어떤 의미에서 상호 평행한 a> 의 최대 집합이다
모든 원시 스큐 격자 S 인자는 그 최대 좌우측 원시 이미지 × 2 S/}S의 섬유화된 산물로 다음과 같이 구성된다Let = A 및 = j B는) 해제된 비빈 A B 의 파티션이며 여기서 모든 와는 한 크기를 공유한다.For each pair pick a fixed bijection from onto . On and separately set and 그러나 B 설정됨
= a= b = = b {\ a b a}, a = b = b = = b= b =b = stylee
where and with belonging to the cell of and belonging to the cell 의 다양한 , 은(는) 코제트 편향이다.This is illustrated in the following partial Hasse diagram where and the arrows indicate the -outputs and from and .

왼손잡이의 원시적인 꼬치 격자를 이중 패션으로 구성한다.모든 오른쪽 [왼쪽]손의 원시적인 꼬치 격자는 이런 방식으로 건설될 수 있다.[3]
스큐 격자의 코셋 구조
Anonrectangular 스큐 격자 S{S\displaystyle}는 최고조의 원시적인 사행 lattices에 의해: 주어진 비교 D{D\displaystyle}A>B{\displaystyle A> -classes; 덮여 있다.A∪ B{A\cup B\displaystyle}S{S\displaystyle}의 최고조의 원시적인 subalgebra고 형성된다 B}S의/D{S/D\displaystyle}. 의 y class는 그러한 하위 지브라에 있다.이 원시 아발그라의 코제트 구조는 최소한 y y과 x y{\ x과 y{\}이(가){{\\ 에 따라 비교할 때 y x y y}은는) -probles 사례보다 약간 덜 직접적인 방식으로 코세트와 그 반대들에 의해 일반적으로 결정된다.특히 D클래스 J에 가입하고 에서 M 을(를) 만나는 비할 데 없는 D클래스 A와 B의 두 코제트 분해 사이에 흥미로운 연관성이 생긴다[4]

따라서 스큐 격자는 이들 사이의 격자와 코셋 편향의 정점에 배치된 직사각형 스큐 격자의 코셋 지도책자로 볼 수 있으며, 후자는 각 코셋 편향과 각 코셋 편향 사이의 부분 이형성으로 볼 수 있다.이 원근법은 본질적으로 스큐 격자의 하세 다이어그램을 주는데, 비교적 순서가 작은 경우 쉽게 그려진다.(위 섹션 3의 다이어그램을 참조하십시오.) 에 있는 D A > > C{\A>의 체인으로 볼 때 하나는 A에서 B로, B에서 C로, 그리고 A에서 C로 세 가지 코제트 편향 세트가 있다.일반적으로 코제트 편향 : → B : 및: : → 부분적 편향 구성 bi { {\은(는) 비워 둘 수 있다.그렇지 않다면, 한 코셋 바이어스 :A→ : ⊆ {{} \\psi Again, , χ, χ, \}}은 의 한 쌍의 편향이다.) 포함은 엄격할 수 있다.S가 범주형일 때, 이는 항상 동일하다(S가 범주형일 때 정확히 주어진 skew 이 경우 각 직사각형 D클래스에 식별 지도를 포함시키고 적절히 비교 가능한 D클래스 사이의 빈 편차와 인접하여 그 사이에 직사각형 알헤브라와 코제트 편차의 범주를 가진다.섹션 3의 간단한 예는 범주형이다.
참고 항목
참조
- ^ a b 리치, J, 링의 스큐 격자, 대수 유니버설리스, 26 (1989), 48-72.
- ^ 요르단, P. 우버 니콜코메트테이티브 버번드, 아치.수학. 2 (1949), 56–59.
- ^ a b c d e 리치, J, 링의 스큐 격자, 대수 유니버설리스, 26 (1989), 48-72
- ^ a b c d Leech, J, Semigroup Forum, 52(1996), 7-24.
- ^ 리치, J, 매직 스퀘어, 유한 평면과 단순한 퀘이실라티, 아르스 콤비나토리아 77(2005), 75-96.
- ^ a b 리치, J, 스큐 래티스의 기하학, 세미그룹 포럼, 52년(1993) 7-24.
- ^ 리치, J, 노멀 스큐 래티스, 세미그룹 포럼, 44(1992), 1-8.
- ^ a b Cvetko-Vah, K, 꼬치 격자의 내부 분해, 대수에서의 통신, 35(2007), 243-247
- ^ a b c 스핑크스의 정리, 세미그룹 포럼 73(2006), 267-272의 새로운 증거.
- ^ a b c 라슬로, G, 리치, J, 그린의 비협조적 격자 관계인 액타 사이언스.수학. (szezed), 68 (2002), 501-533.
- ^ a b 스핑크스, M, 비확정 격자 이론의 자동 공제, 테크.보고서 3/98, Monash U, GSCIT, 1998
- ^ 스핑크스, M, 비확정 격자 이론의 자동 공제, 테크.보고서 3/98, 모나시 대학교, Gippsland 컴퓨팅 및 정보 기술 학교, 1998년 6월
- ^ a b 스핑크스, M, 스큐 래티스에 대한 중간 유통성, Semigroup Forum 61(2000), 341-345.
- ^ 크베토바, 카린; 키욘, M.; 리치, J.; 스핑크스, 스큐 라티스의 M. 취소.주문 28(2011), 9-32.
- ^ Bignall, R. J. Quasiprimal Variet and Components of Universal Algebras, Statement, The Flinders University of South Australia, 1976년.
- ^ Bignall, R J, 비확정 다변량 논리학, Proc. 21차 다변량 논리학 국제 심포지엄, 1991년 IEEE 컴퓨터 Soc.프레스, 49-54
- ^ 비그놀, R J, J 리치, 스큐 부울 알헤브라와 판별자 품종, 대수 유니버설리스, 33 (1995), 387-398.
- ^ Bignall, R J 및 M Spinks, Proposal scret Boolean logic, Proc. 26차 다변량 논리 국제 심포지엄, 1996, IEEE 컴퓨터 Soc.43-48번으로
- ^ 비그놀, R J, M 스핑크스, 굴곡 BCS-알지브라 부교구, 사이언티애 수학자포니아, 58(2003년), 629-638.
- ^ Bignall, R J, M Spinks, On 2진 판별기 품종 (I): 내연성 BCS-algebras, International Journal of Malge and Computing이 등장.
- ^ 코니쉬, W H, 부울 꼬치 알헤브라스, 액타 수학. 아카드. 공상과학. 흥, 36 (1980), 281-291.
- ^ 리치, J, 스큐 부울 알헤브라스, 대수유니버설리스, 27(1990), 497-506.
- ^ a b 리치와 스핑크스, 일반화된 부울알헤브라스, 대수유니버설리스 58(2008), 287-302, 307-311에서 생성된 스큐 부울알헤브라스.
- ^ 스핑크스, M, 2002년 모나시 대학 논문 사전 BCK 알헤브라스 이론에 기여
- ^ 스핑크, M 및 R Veroff, 꼬치 부울 명제 미적분, J. 자동 추론, 37(2006), 3-20.
- ^ Cvetko-Vah, K, Skew 격자 매트릭스 링, 대수 유니버설리스 53 (2005), 471-479.
- ^ Cvetko-Vah, K, 링의 순꼬치 선반, Semigroup Forum 68(2004), 268-279.
- ^ 세베코바, K, 퓨어 ∇-밴드, 세미그룹 포럼 71(2005), 93-101.
- ^ C벳코-바, K, 스큐 래티스 반지, 논문, Ljubljana 대학교, 2005.
- ^ Cvetko-Vah, K, J Leech, ∇-operation on the ring in bands, Sem그룹 포럼 76(2008), 32-50

 (가) 장착된 세트 S이다.
(가) 장착된 세트 S이다.



 경우
경우 







 의해 주어진다
의해 주어진다





























 L
L 













 하위
하위  이형성이다.S/D \leq \aleph_0에 대한 모든 대칭 스큐 래티스는 격자 섹션을 허용한다.
이형성이다.S/D \leq \aleph_0에 대한 모든 대칭 스큐 래티스는 격자 섹션을 허용한다.![T[R]=\bigcup _{{t\in T}}R_{t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7402d9235b1121a93d7e946e6e2b554ab2c1d212)
![T[L]=\bigcup _{{t\in T}}L_{t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/077f1c59c220dd2fe74c40c4d529024eeaa32f76)



![{\displaystyle T[R]\subseteq S\rightarrow S/L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e04de208aa74e9352e312b41decdf8b905426f1a)
![{\displaystyle T[L]\subseteq S\rightarrow S/R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dbeca5a8902c6c867ff5b7e1ab8371294e05f63) 이형성이다.
이형성이다.
































 후자는 부울 격자 x 0 x
후자는 부울 격자 x 0 x




















































 (는) 코제트 편향이다.This is illustrated in the following partial Hasse diagram where
(는) 코제트 편향이다.This is illustrated in the following partial Hasse diagram where 


 x
x y
y

 있는 D
있는 D 







