노즈콘 디자인

이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2018년 7월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

압축 가능한 유체 매체(로켓이나 항공기, 미사일 또는 탄환 등)를 통해 이동하도록 의도된 차량이나 차체의 노즈콘 부분의 공기역학적 설계 문제를 고려할 때, 최적의 성능을 위해 노즈콘 기하학적 형태를 결정하는 것이 중요한 문제다. 많은 애플리케이션에서, 그러한 작업은 그러한 유동적 매체를 통한 신속한 움직임에 대한 최소한의 저항을 경험하는 회전 형태의 고체의 정의를 필요로 한다.

노즈콘 모양 및 방정식

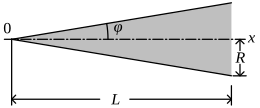
일반 치수

다음의 모든 노즈콘 모양 방정식에서 L은 노즈콘의 전체 길이, R은 노즈콘 밑면의 반지름이다. y는 임의의 지점 x에서 반경이며, x는 노즈콘 끝에서 L까지 다양하다. 이 방정식은 코 모양의 2차원 프로필을 정의한다. 노즈콘의 회전 전체는 중심선을 중심으로 종단을 회전하여 형성된다. ½L. 방정식이 '완벽한' 모양을 설명하는 반면, 실용적인 코뿔소들은 제조나 공기역학적 이유로 종종 흐물흐물해지거나 잘린다.^[1]

코닉

매우 흔한 코뿔 모양은 단순한 원뿔형이다. 이 모양은 종종 제조의 용이성을 위해 선택된다. 보다 최적화되고 능률화된 모양(아래 설명)은 훨씬 더 만들기 어려운 경우가 많다. 원뿔형 종단의 옆면은 직선이므로 직경 방정식은 다음과 같다.

${\displaystyle y={xR \over L}}$

원뿔은 때때로 반각 ,으로 정의된다.

${\displaystyle \varphi }$= ${\displaystyle \arctan }$ ${\displaystyle }$(${\displaystyle \frac{R}{}}$ L ${\displaystyle )}${\$displaystyle \phi =\arctan \left({R \over L}\right)}$ 및 $y$ = x ${\displaystyle \tan }$ ${\displaystyle (\varphi )}$ ${\$y=$x\tan$(\phi $)\;}$

완곡한 원추형

실용적인 응용에서 원뿔형 코는 종종 구의 한 부분으로 그것을 막음으로써 무뎌진다. 구체와 원뿔이 만나는 접선점은 다음에서 찾을 수 있다.

${\displaystyle x_{t}={\frac {L^{2}}{R}{\sqrt {\r_{n}^{2}}{R^{R^{2}+L^{2}}}}}}$

${\displaystyle y_{t}={\frac {x_{t}R}{{}}{L}}$

여기서 r은_n 구형 노즈 캡의 반지름이다.

구형 노즈 캡의 중심인 x는_o 다음에서 찾을 수 있다.

${\displaystyle x_{o}=x_{t}+{\sqrt {r_{n}^{2}-y_{t}^{2}}:$

그리고 꼭지점인 x는_a 다음에서 찾을 수 있다.

${\displaystyle x_{a}=x_{o}-r_{n}}}$

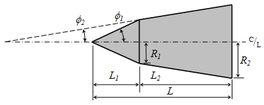
바이코닉

바이코닉 노즈콘 모양은 단순히 길이₂ L의 원뿔(일반적으로 원뿔형 전이단면 모양) 위에 길이₁ L이 쌓여 있는 원뿔 모양이며, 여기서 상단 원뿔의 밑부분은 반지름 R에서₁ 베이스 반경 R과₂ 더 작은 원뿔의 위쪽 반경이 같다.

${\displaystyle L=L_{1}+L_{2}}$

${\displaystyle 0}$ ${\displaystyle \le }$ x ${\displaystyle \le }$ ${\displaystyle {L\mathrm{}}_{}}$ 1 ${\$ x$\leq L_{1$} $$: $y{\displaystyle }$= ${\displaystyle x\frac{}{}}$ ${\displaystyle \frac{{}_{}}{}}$ 1 ${\displaystyle \frac{{}_{}}{{}_{}}}$ ${\displaystyle \frac{{1\mathrm{}}_{}}{}}$ ${\$

For ${\displaystyle L_{1}\leq x\leq L}$ : ${\displaystyle y=R_{1}+{(x-L_{1})(R_{2}-R_{1}) \over L_{2}}}$

반각:

${\displaystyle {\varphi 1\mathrm{}}_{}}$= ${\displaystyle \mathrm{아크탄}}$$$${\displaystyle (}$$R$ ${\displaystyle \frac{{1\mathrm{}}_{}}{}}$ ${\displaystyle \frac{{L\mathrm{}}_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$) ${\$} $\over L_{1}\$1}\$right)}$${\displaystyle }$및 $y$ =$x tan$ $({R_{1}){\displaysty1$}

${\displaystyle \phi _{2}=\arctan \left({R_{2}-R_{1} \over L_{2}}\right)}$ and ${\displaystyle y=R_{1}+(x-L_{1})\tan(\phi _{2})\;}$

탄젠트 오기브

단순한 원추형 옆에는 접선 오기형 모양이 취미용 로켓에서 가장 친숙하다. 이 모양의 프로필은 로켓 본체가 밑부분의 노즈콘 곡선에 접하고, 밑부분은 원의 반지름에 닿도록 원의 한 부분으로 형성된다. 이 모양이 인기를 끈 것은 단순히 원형 단면이기 때문에 프로파일 구성이 용이하기 때문이다.

오기를 형성하는 원의 반지름을 오기 반지름, ρ이라고 하며, 다음과 같은 공식으로 표현되는 노즈콘의 길이와 기저 반지름과 관련이 있다.

${\displaystyle \rho ={R^{2}+L^{2} \2R}}이상 \}$

x가 0에서 L까지 변화하므로 임의의 지점 x에서 반경 y는 다음과 같다.

${\displaystyle y={\sqrt {\rho^{2}-(L-x)^{2}}+R-\rho }$

노즈콘 길이 L은 ρ보다 작거나 같아야 한다. 만약 그것들이 같다면, 그 모양은 반구형이다.

스패럴한 탄젠트 오기브

톡 쏘는 오기 코는 종종 구의 한 부분으로 그것을 덮음으로써 무뎌진다. 구가 접선 오기를 만나는 접선점은 다음에서 찾을 수 있다.

${\displaystyle {\begin{aligned}x_{o}&=L-{\sqrt {\left(\rho -r_{n}\right)^{2}-(\rho -R)^{2}}}\\y_{t}&={\frac {r_{n}(\rho -R)}{\rho -r_{n}}}\\x_{t}&=x_{o}-{\sqrt {r_{n}^{2}-y_{t}^{2}}}\end{aligned}}}$

여기서 r은_n 반지름이고 x는_o 구형 노즈캡의 중심이다.

마지막으로, 꼭지점은 다음에서 찾을 수 있다.

${\displaystyle x_{a}=x_{o}-r_{n}}}$

오기브자리 세컨트

이 모양의 종단도 원의 한 구획에 의해 형성되지만, 형상의 밑부분은 오기반경에 의해 정의된 원의 반지름에 있지 않다. 로켓 본체는 밑부분의 코의 곡선에 접하지 않을 것이다. 오기 반지름 ρ은 R과 L에 의해 결정되는 것이 아니라(접선 오기를 위한 것이기 때문에), 오히려 코 모양을 정의하기 위해 선택해야 할 요인 중의 하나이다. 만약 제2의 오기 반경이 동일한 R과 L의 탄젠트 오기의 오기 반지름보다 크면, 결과적인 제2의 오기는 베이스의 일부가 잘린 탄젠트 오기로 나타난다.

${\displaystyle \rho >{R^{2}+L^{2} \over 2R}}$ and ${\displaystyle \alpha =\arccos \left({{\sqrt {L^{2}+R^{2}}} \over 2\rho }\right)-\arctan \left({R \over L}\right)}$

그 다음, 임의의 지점에서 x가 0에서 L까지 변화한 반지름 y는 다음과 같다.

${\displaystyle y={\sqrt {\rho ^{2}-(\rho \cos(\reason )-x)^{2}}-\rho \sin(\rho )}$

만약 선택된 ρ이 접선 오기 than보다 작고 노즈콘 길이의 절반보다 크면, 그 결과는 베이스 직경보다 큰 최대 직경까지 튀어나오는 제2의 오기가 될 것이다. 이 모양에 대한 전형적인 예는 정직한 존의 코뿔소다.

${\displaystyle {\frac {L}{2}}}<\rho <{R^{2}+L^{2} \2R}\over 2R}}}$

타원형

이 형태의 종단은 타원의 1/2이며, 주축은 중심선이고 부축은 노즈콘의 밑부분이다. 주요 축에 대해 완전한 타원이 회전하는 것을 프로이트 스피로이드라고 부르기 때문에 타원형 코 모양은 프로이트 반구라고 적절하게 알려져 있을 것이다. 이 모양은 무딘 코와 접선 밑부분 때문에 아음속 비행(모델 로켓 등)에서 인기가 있다.^{[further explanation needed]} 이것은 전문 로켓에서 흔히 볼 수 있는 형태가 아니며, 거의 항상 다른 디자인이 더 적합한 훨씬 높은 속도로 비행한다. 만약 R이 L과 같다면, 이것은 반구다.

${\displaystyle y=R{\sqrt{1-{x^{2} \over L^{2}}}$

포물선

이 코 모양은 사람들이 흔히 "파라볼릭" 코뿔소를 언급할 때 상상되는 뭉툭한 모양이 아니다. 포물선 연속 노즈 모양은 포물선의 한 부분을 그것의 격자 직장에 평행한 선 주위를 돌면서 생성된다. 이 구조는 포물선이 원이 아닌 정의형이라는 점을 제외하면 접선 오기와 비슷하다. 오기에 그렇듯이, 이 구조물은 끝이 뾰족한 코 모양을 만들어 낸다. 일반적으로 포물선 코와 관련된 둔탁한 모양은 아래 파워 시리즈를 참조하십시오. (포물형 모양도 타원형 모양과 혼동되는 경우가 많다.)

For ${\displaystyle 0\leq K'\leq 1}$ : ${\displaystyle y=R\left({2\left({x \over L}\right)-K'\left({x \over L}\right)^{2} \over 2-K'}\right)}$

K′는 0과 1 사이의 어느 곳에서나 다를 수 있지만, 노즈콘 모양에 사용되는 가장 일반적인 값은 다음과 같다.

포물선형	K′ 값
원뿔	0
절반	1/2
3쿼터	3/4
가득찬	1

풀 포물선(K′ = 1)의 경우 형상은 그 밑부분에서 몸에 접하고, 밑부분은 포물선 축에 있다. K′의 값이 1보다 작을수록 날씬한 모양이 되며, 그 외모가 오귀브와 유사하다. 형상은 더 이상 밑면에 접하지 않고, 밑면은 포물선의 축과 평행하나 상쇄된다.

파워 시리즈

파워 시리즈 노즈콘 모양을 보여주는 그래프

절반(n = 1/2) 3분기(n = 3/4)

파워 시리즈는 일반적으로 '파라볼릭' 노즈콘으로 언급되는 형태를 포함하지만 포물선 노즈콘으로 정확하게 알려진 모양은 포물선 노즈콘(위 설명)의 일원이다. 파워 시리즈 모양은 끝이 뭉툭하고, 밑부분이 차체 튜브에 접하지 않는 것이 특징이다. 노즈콘과 신체 사이의 관절에는 항상 불연속성이 존재하는데, 이것은 분명히 비역학적으로 보인다. 이 불연속성을 부드럽게 하기 위해 밑부분에서 모양을 수정할 수 있다. 납작한 면의 실린더와 원뿔은 모두 동력 시리즈의 구성원인 형상이다.

파워 시리즈 노즈 모양은 n 값이 1 미만인 경우 x축에 대해 y = R(x/L)ⁿ 곡선을 회전시켜 생성된다. n 인자는 형상의 무뚝뚝함을 조절한다. n 값이 약 0.7 이상일 경우 팁은 상당히 날카롭다. n이 0으로 줄어들면서 파워 시리즈 코 모양이 점점 무뎌진다.

0 ${\displaystyle \le n}$ ${\displaystyle \le }$ ${\displaystyle 1}$ ${\displaystyle 0\leq$ n$\leq 1$ $y{\displaystyle }$= R${\displaystyle {}^{}}$ ${\displaystyle {\frac{L}{}}^{}}$) n ${\$$x \over$ L$}\오른쪽$)$^{n}}}$

n의 공통 값에는 다음이 포함된다.

전원 유형	n 값
실린더	0
절반 (파라볼라)	1/2
3쿼터	3/4
원뿔	1

해크 시리즈

Hack 시리즈 노즈콘 모양을 보여주는 그래프

LD-하크(본 카르만) (C = 0) LV-해크(C = 1/3)

위의 모든 노즈콘 모양과 달리 볼프강 하크의 직렬 모양은 기하학적 형상으로 구성되지 않는다. 모양은 대신 항력을 최소화하기 위해 수학적으로 도출된다. 유사한 파생을 가진 관련 모양은 Sears-Hack 몸통이다. 시리즈는 아래 방정식에서 C의 값으로 결정된 연속적인 형상 집합이지만, C의 두 값은 특별한 의미를 가진다: C = 0일 때, 표기 LD는 주어진 길이와 직경에 대한 최소 항력을 의미하며, C = 1/3일 때 LV는 주어진 길이와 부피에 대한 최소 항력을 나타낸다. Hack 시리즈 노즈콘은 C = 2/3인 경우를 제외하고 베이스에서 완전히 몸에 접하지 않는다. 그러나 불연속성은 보통 너무 경미하여 감지할 수 없다. C > 2/3의 경우, Hack nose cones는 base 직경보다 큰 최대 직경으로 팽창한다. 엉덩이 코끝은 뾰족한 끝이 아니라 약간 둥글다.

${\displaystyle {\begin{aigned}\theta &=\arccos \left(1-{2x \over L}\오른쪽)\\y&={R \over {\sqrt {\pi }}{\sqrt {\\theta -{\\sin(2\theta ) \{3}(\theta )}}}}}$

C의 특수 값(위에서 설명한 바와 같이)은 다음을 포함한다.

해크 시리즈 유형	C 값
LD-하크 (본 카르만)	0
LV-해크	1/3
접선	2/3

폰 카르만

Hack 시리즈 설계는 주어진 길이와 직경에 대해 최소 항력을 제공하는 LD-Hack 설계로, C = 0은 일반적으로 Von Karrman 또는 Von Karrman Ogive라고 불린다.

에어로스피크

노즈콘 드래그 특성

항공기와 로켓의 경우, 마하 .8 이하에서, 코 압력 끌기는 모든 모양에서 본질적으로 0이다. 주요 중요 인자는 마찰 드래그인데, 마찰 드래그는 주로 습윤 부위, 그 부위의 표면의 부드러움, 형상의 불연속부의 유무에 의존한다. 예를 들어, 엄격히 아음속 로켓에서는 짧고 무뚝뚝하며 매끄러운 타원형 모양이 보통 가장 좋다. 압력 항력이 급격히 증가하는 트랜스닉 영역과 그 이상에서는 항력에 대한 코 모양의 영향이 매우 커진다. 압력 항력에 영향을 미치는 요인은 노즈콘의 일반적인 모양, 미세도 비율, 허세비 등이다.^[2]

일반형상의 영향

노즈콘 설계에 대한 많은 참고문헌에는 다양한 비행체에서 다양한 코 모양의 드래그 특성을 비교한 경험적 데이터가 포함되어 있다. 여기에 표시된 도표는 가장 관심 있는 비행 체계에 대한 데이터를 가장 포괄적이고 유용한 것으로 보인다.^[3] 이 차트는 일반적으로 다른 참조 자료(특히 USAF Datcom)에서 발견된 보다 상세하지만 덜 포괄적인 데이터에 동의한다.

많은 노즈콘 설계에서 가장 큰 관심사는 마하 0.8에서 마하 1.2까지의 트랜소닉 영역에서의 비행 성능이다. 트랜소닉 영역의 많은 도형에 데이터를 사용할 수 없지만, 표에는 이러한 목적을 위해 인기 있는 원뿔형 또는 오기형 도형보다 Von Karrman 도형 또는 n = 1/2 도형의 파워 시리즈 도형이 더 바람직하다는 것이 분명하게 제시되어 있다.

이러한 관찰은 원뿔형 코가 '기계 깨기'에 가장 적합하다는 흔히 되풀이되는 통념에 어긋난다. 전투기는 항전술과 인렛트의 다른 고려사항들에 의해 종종 그들의 코 모양이 왜곡되지만, 아마도 트랜소닉 부위에 최적화된 코 모양의 좋은 예일 것이다. 예를 들어, F-16 파이팅 팔콘 코는 폰 카르만 모양과 매우 가까운 것으로 보인다.

미세화 비율의 영향

노즈콘 길이와 기저 직경의 비율을 정밀도비라고 한다. 이 용어는 보통 날개와 꼬리에 적용되지만, 이것을 가로 세로 비율이라고도 한다. 전체 길이와 직경을 고려해 차량 전체에 미세한 비율을 적용하는 경우가 많다. 길이/직경관계는 흔히 노즈콘의 경량이라고도 한다.

초음속에서는 미세한 비율이 특히 낮은 비율의 노즈콘파 항력에 상당한 영향을 미치지만 5:1 이상으로 증가하는 비율에 대한 추가 이득은 거의 없다. 미세도가 높아지면 습윤 부위, 따라서 드래그의 피부 마찰 성분도 증가한다. 따라서 최소 항력 미세화 비율은 궁극적으로 감소하는 파동 항력과 증가하는 마찰 항력 사이의 트레이드오프가 될 것이다.

추가 읽기

• Haack, Wolfgang (1941). "Geschoßformen kleinsten Wellenwiderstandes" (PDF). Bericht 139 der Lilienthal-Gesellschaft für Luftfahrtforschung: 14–28. Archived from the original (PDF) on 2007-09-27.
• U.S. Army Missile Command (17 July 1990). Design of Aerodynamically Stabilized Free Rockets. U.S. Government Printing Office. MIL-HDBK-762(MI).

참조