핀 그룹

수학에서 핀 그룹은 2차 공간과 연관된 클리포드 대수학의 특정 부분군이다. 스핀 그룹이 특수 직교 그룹에 2대 1로 매핑하는 것처럼 직교 그룹에 2대 1로 매핑한다.

일반적으로 핀 그룹에서 직교 그룹까지의 지도가 위나 범용 커버 공간은 아니지만, 2차 형태가 확실하다면(그리고 치수가 2보다 크면), 둘 다다다.

커널의 비경쟁 요소는-1,{\displaystyle-1,}으로 표시되며, 일반적으로 원점을 통한 반사의 직교 변환과 혼동해서는 안 된다-나는.{\displaystyle-.}

일반적 정의

$V{\displaystyle }$ ${\displaystyle V}$을(를) 비분할 2차 형식 $Q{\displaystyle }$ ${\displaystyle Q$의 벡터 공간이 되도록$$ 하십시오. The pin group ${\displaystyle \operatorname {Pin} (V,Q)}$ is the subset of the Clifford algebra ${\displaystyle \operatorname {Cl} (V,Q)}$ consisting of elements of the form ${\displaystyle v_{1}v_{2}\cdots v_{k}}$, where the ${\displaystyle v_{i}}$ are vector이러한 $경우{\displaystyle }$ Q${\displaystyle (v_{}}$ i${\displaystyle {}_{}}$)${\displaystyle }$=${\displaystyle }$± ${\displaystyle 1}$ ${\displaystyle$ Q$(v_{i}}=\pm$ 1$\}.$ 스핀 그룹 ${\displaystyle \mathrm{스핀}(V}$, Q${\displaystyle }$) ${\displaystyle \operatorname {Spin}(V,Q)}$은(는) 유사하게 정의되지만$$ $k{\displaystyle }$ ${\displaystyle$ k$}$은(는) 짝수로 제한되어$$ 핀 그룹의 하위 그룹이다.^[1]

이 글에서 $V{\displaystyle }$ ${\displaystyle V}$은(는) 항상 실제 벡터 공간이다$$. When ${\displaystyle V}$ has basis vectors ${\displaystyle e_{1},...,e_{p+q}}$ satisfying ${\displaystyle e_{1}^{2},...,e_{p}^{2}=1}$ and ${\displaystyle e_{p+1}^{2},...,e_{p+q}^{2}=-1,}$ the pin group is PIN(p, q)으로 표시됨.

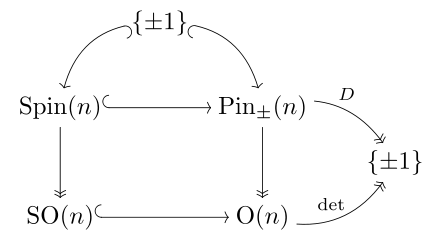
Geometrically, for vectors ${\displaystyle v}$ with ${\displaystyle Q(v)\neq 0}$, ${\displaystyle -vwv^{-1}}$ is the reflection of a vector ${\displaystyle w}$ across the hyperplane orthogonal to ${\displaystyle v}$. More generally, an element ${\displays$$tyle v_{1}v_{2}\cdots v_{k}}$ of the pin group acts on vectors by transforming ${\displaystyle w}$ to ${\displaystyle (-1)^{k}v_{1}v_{2}\cdots v_{k}w(v_{1}v_{2}\cdots v_{k})^{-1}}$, which is the composition of k reflections. 모든 직교 변환은 반사의 구성(Cartan-Dieudonné 정리)으로 표현할 수 있기 때문에, 핀 그룹의 이러한 표현은 핀 그룹에서 직교 그룹에 이르는 동형상이라는 것을 따른다. 이것은 종종 꼬인 부선 표현이라고 불린다. 핀 그룹의 요소 ±1은 ID $I{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle O(p,}$ ${\displaystyle q}$) ${\displaystyle$ I$\in O(p,q$에 매핑되는 요소로서, O(p, q)의 모든 요소는 정확히 핀(p, q)의 두 요소에 해당한다.^[2]

확정형식

한정된 형태의 핀 그룹은 직교 그룹에 매핑되며, 각 구성 요소는 직교 그룹을 이중으로 덮는 단순하게 연결된다. 양의 확정 2차 형태 Q와 음의 -Q에 대한 핀 그룹은 이형성이 아니라 직교 그룹이다.^{[note 1]}

표준형식으로 보면 O(n, 0) = O(0, n)이지만 핀(n, 0)과 핀(0, n)은 일반적으로 이형성이 아니다. ${\displaystyle {클리포드\mathrm{}}^{}}$ 알헤브라스(여기서 v 2 =${\displaystyle {}^{}}$Q ${\displaystyle (v}$) ${\displaystyle \in }$ ${\displaystyle \mathrm{C}}$ l${\displaystyle }$(${\displaystyle V}$, ${\displaystyle Q}$) ${\displaystyle v^{2}=Q(v)\in \mathrm {Cl}(V,Q)})$에 대한 "+" 기호 규칙을 사용하여 쓰기

${\displaystyle {\mbox{Pin}_{+}(n):={\mbox{Pin}}(n,0)\qquad {\mbox{Pin}_{-}(n):={\mbox{PIN}(0,n)}$

그리고 이 두 가지 모두 O(n) = O(n, 0) = O(0, n)에 매핑된다.

대조적으로 우리는 자연 이형성^{[note 2]} 스핀(n, 0) ≅ 스핀(0, n)을 가지고 있으며, 둘 다 n ≥ 3의 (유일한) 범용 커버인 특수직교군 SO(n)의 (유일한) 비삼각형 이중 커버다.

무기한 서식

이 구간은 확장이 필요하다. 덧셈으로 도와줘도 된다.(2009년 12월)

O(p, q)의 서로 다른 이중커버가 8개 있는데, p의 경우 q ≠ 0으로 C에₂ 의한 중심(C₂ × C 또는₂ C₄)의 확장에 해당한다. 그들 중 단 두 명만이 핀 그룹이다. 즉 클리포드 대수학을 대표적으로 인정하는 그룹이다. 각각 Pin(p, q)과 Pin(q, p)으로 불린다.

위상학군으로서

연결된 모든 위상학 그룹은 위상학 공간으로서 독특한 유니버설 커버를 가지고 있으며, 이 커버는 기본 그룹에 의한 중앙 확장으로서 독특한 그룹 구조를 가지고 있다. 단절된 위상학 집단의 경우, 집단의 정체성 구성요소에 대한 고유한 보편적 커버가 있으며, 다른 구성요소(정체성 구성요소에 대한 주된 동질적 공간)의 위상학적 공간과 동일한 커버를 취할 수 있지만, 다른 구성요소의 그룹 구조는 일반적으로 고유하게 결정되지 않는다.

핀 및 스핀 그룹은 클리포드 알헤브라스에서 온 직교 및 특수 직교 그룹과 관련된 특정 위상학 그룹이다. 다른 이중 커버 또는 다른 구성 요소의 다른 그룹 구조에 해당하는 다른 유사한 그룹이 있지만 핀 또는 스핀 그룹이라고 부르지는 않으며 많은 연구도 하지 않는다.

2001년에 Andrzej Trautman은^{[note 3]} O(p) x O(q)의 32개의 불평등 이중 커버 집합, O(p, q)의 최대 콤팩트 서브그룹, 그리고 동일한 그룹 O(p, q)의 8개의 이중 커버를 명시적으로 구성했다.

건설

두 핀 그룹은 두 개의 중앙 확장자에 해당한다.

${\displaystyle 1\to \{\pm 1\}\to {\mbox{Pin}_{\pm }(V)\to 1.}$

스핀(V)의 그룹 구조(결정요인 1의 연결된 구성요소)는 이미 결정되었고, 다른 구성 요소의 그룹 구조는 중심까지 결정되므로 ±1의 모호성을 가진다.

두 개의 확장은 ±1 ∈ Ker (Spin(V) → SO(V))에 대한 반사 사각형의 사전 이미지로 구분되며, 그에 따라 두 핀 그룹의 이름이 지정된다. O(V), r2)1에서 명시적으로, 다른 모습이 주문 2(그것은 결정 하나)Spin±(V)→ SO(V)의 커널 내에서 주어야 하는 반사의 preimage의 제곱, 그렇게 r일 2cm±1{\displaystyle{\tilde{r}}^{2}=\pm 1}고, 한쪽의 선택은 핀 그룹(접형골 후두골 연골 결합(V의 요소로 채택된 이래 모두 정해집니다 켤레)을 결정한다면 whic다.h 연결된다. 모든 반사는 동일한 값으로 정사각형을 이루어야 한다.)

구체적으로는₊ $핀$에서 r${\displaystyle \stackrel{}{}}$~ ${\${\$tilde{r}}$의 순서 2가 있으며$$, 부분군 {1, r}의 프리이미지는₂ C × C₂: 동일한 반사를 두 번 반복하면 정체성을 얻는다.

핀에서₋ $r{\displaystyle \stackrel{}{}}$~ ${\$은(는) 순서 4를 가지며$$, 부분군 {1, r}의 프리이미지는₄ C: 동일한 반사를 두 번 반복하면 "2˚ 회전" 즉, 스핀(V) → SO(V)의 비전위 요소를 "2˚ 회전"으로 해석할 수 있다(각 축이 동일한 원소를 산출함).

저차원

1차원에서는 핀 그룹이 첫 번째 다이헤드 및 다사이클릭 그룹과 일치한다.

${\displaystyle {\begin{aligned}{\mbox{Pin}}_{+}(1)&\cong \mathrm {C} _{2}\times \mathrm {C} _{2}={\mbox{Dih}}_{1}\\{\mbox{Pin}}_{-}(1)&\cong \mathrm {C} _{4}={\mbox{Dic}}_{1}.\end{정렬}}}$

2차원에서 핀과₊ 핀의₋ 구별은 2n곤의 다이헤드 그룹과 C의_2n 다사이클릭 그룹과의 구별을 반영한다.

핀에서₊, 부분군 Dih_n < O>(2)로 간주되는 n곤의 이면군 프리이미지는 2n곤, Dih_2n < Pin₊(2)의 이면군이며, 이면군₋ 프리이미지는 Dic_n < Pin₋(2)이다.

The resulting commutative square of subgroups for Spin(2), Pin₊(2), SO(2), O(2) – namely C_2n, Dih_2n, C_n, Dih_n – is also obtained using the projective orthogonal group (going down from O by a 2-fold quotient, instead of up by a 2-fold cover) in the square SO(2), O(2), PSO(2), PO(2), though in this case it is also realized geometrically, as "the projectiviz원 안의 2n곤은 투영 선에 있는 n곤이다."

3차원에서 상황은 다음과 같다. +1의 3개의 항공명 제곱근에 의해 생성되는 클리포드 대수학은 2×2 복합 행렬의 대수로서₊ 핀(3)은${\displaystyle }${ ${\displaystyle A}$u${\displaystyle }$U (${\displaystyle 2}$ )${\displaystyle }$: ${\displaystyle det}$A${\displaystyle }$= ± ${\displaystyle 1}$ ${\displaystyle \}}${\$displaystyle$\{$A\in$U($2):\det$ A$=\pm 1$^[3] -1의 3개의 항공명 사각근에 의해 생성된 클리포드 대수학은 ${\displaystyle 대수\mathbb{}}$ H ${\displaystyle \oplus }$ H ${\$ \oplus $\mathb {H$ 핀₋(3)은 이형체로서 SU(2) × C이다₂. 핀₊₋(3)의 중심은₄₂ C이고 핀(3)의 중심은 C × C이기₂ 때문에 이러한 그룹은 비이형적이다.

중심

핀(n,0)의 중심 = n이₊ 짝수일 때는 C₂, n = 1모드₂ 4, n = 3모드 4일 때는 C이다₂₄. 핀(0,n)의 중심₋ = n이 짝수일 때는 C, n₂ = 1모드 4일 때는 C₄₂, n = 3모드 4일 때는 C × C이다₂. p의 경우, q ≠ 0 핀(p,q)의 중심은 C에₂ 의한 C₂ × C 또는₂ C의₄ 확장이다.

이름

이 이름은 (Atiyah, Bott & Shapiro 1964, 3, 17페이지)에서 소개되었는데, 그들은 "이 농담은 J-P 덕분이다. 세레" 스핀: "핀은 O(n)로, 스핀은 SO(n)로," 따라서 "스핀"에서 "S"를 떨어뜨리면 "핀"이 나온다.

메모들

참조