빛의 궤도 각도 운동량

빛의 궤도 각도운동량(OAM)은 양극화가 아닌 자기장 공간 분포에 의존하는 광선의 각도운동량 성분이다.내부 OAM과 외부 OAM으로 더 분할할 수 있다.내부 OAM은 광선의 원점에 독립적인 각운동량으로서 나선형 또는 비틀어진 파동과 연관될 수 있다.외부 OAM은 광선 위치(빔의 중심)의 교차 생산물로 얻을 수 있는 원점에 의존하는 각운동량과 그 총 선형운동량이다.null

소개

빛의 빔은 선형 $운동량{\displaystyle \mathbf{}}$ P$[\$을(를) 운반하므로 외부 각도 $운동량{\displaystyle {\mathbf{}}_{}}$ L ${\displaystyle {}_{}}$= ${\displaystyle r\mathbf{}}$ ${\displaystyle \times }$ ${\displaystyle P\mathbf{}}$ ${\${$P}}$으로 귀인할 수 있다$.$ 이 외부 각도 운동량은 좌표의 원점에 따라 달라진다.빔 축에서 원점을 선택하고 빔이 원통형 대칭(적어도 모멘텀 분포에서)이면 외부 각운동량이 사라진다.외부 각운동량은 양극화와 무관하고 광학장(E)의 공간 분포에 따라 달라지기 때문에 OAM의 일종이다.null

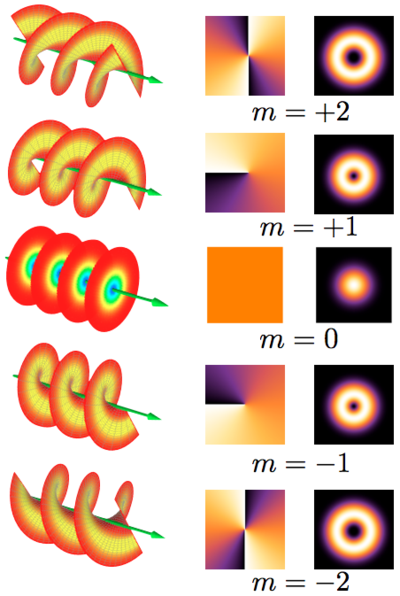
보다 흥미로운 OAM의 예는 근축 광선이 소위 "헬리컬 모드"에 있을 때 나타나는 내부 OAM이다.전자기장의 헬리컬 모드는 빔 축에서 중앙에 광학적 소용돌이가 있는 나선형 모양의 파전선이 특징이다(그림 참조).헬리컬 모드는 정수 $m{\displaystyle }$ ${\displaystyle m$ 양수 또는 음수로 특징지어진다.$m{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle m=0$인 경우 모드는 나선형이 아니며 파장프롱트는 병렬 평면의 시퀀스(예: "평면파"라는 이름)와 같은 여러 개의 분리된 표면이다.${\displaystyle \mathrm{만약}}$ m${\displaystyle }$=${\displaystyle }$± 1 ${\$$displaystyle m=\$$pm 1$$}$의 부호에 의해 결정된 $손길이,$ 파장은 단일 나선 표면의 형태로, 스텝 길이는 파장 $\lambda {\displaystyle }$ ${\displaystyle \lambda }$과 같다$.$ ${\displaystyle 만약}$ m ${\displaystyle ⩾}$ ${\displaystyle 2}$ ${\displaystym$m$\geqslant$ 2$\}$이면, 파장은 m ${\displaystyle \{}$${\displaystyle m}$으로 구성된다.$\displaystyle$m$}$ 구별되지만$$ 서로 얽혀 있는 나선형이며, 각 나선 표면의 층계 ${\displaystyle 길이}$는 m ${\displaystyle \lambda }${\$displaystyle$ m$}$과 같고$,$ $m{\displaystyle }${\$displaystyle m}$ 기호로 주어진 손길이$.$정수 $m{\displaystyle }$ ${\displaystyle m}$은 광학적 소용돌이의 이른바 "위상 전하"이기도$$ 하다.헬리컬 모드인 광선은 0이 아닌 OAM을 전달한다.null

오른쪽 그림에서 첫 번째 열은 빔 파전면 모양을 보여준다.두 번째 열은 잘못된 색상으로 표시된 빔 단면에서의 광학적 위상 분포다.세 번째 열은 빔 단면에서의 광도 분포(검은 소용돌이 중심 포함)이다.null

예를 들어, 회전 모드 $번호{\displaystyle }$ l${\displaystyle 0}$ 0$[\displaystyle$ l$\neq$ 0$}$을(^[1]를) 가진 모든 Laguerre-Gaussian 모드는 그러한 나선형 파형을 가지고$$ 있다.null

빛의 궤도 각도 운동량에 대한 수학적 표현

근축 한계에서^{[dubious – discuss]} 궤도 각도 운동량의 고전적인 표현은 다음과 같다.^[2]

${\displaystyle \mathbf {L} =\epsilon _{0}\sum _{i=x,y,z}\int \left(E^{i}\r}\mathbf {r}\times \mathbf {\\\nabla \rig)A^{i}\오른쪽)d^{3}\mathbf {r},}$

여기서 $E{\displaystyle \mathbf{}}$ ${\$과(와) $A{\displaystyle \mathbf{}}$ ${\$는) 전기장과 벡터 전위, , ${\$은 진공 허용률이며 SI 단위를 사용하고 있다.$i{\displaystyle }$ ${\displaystyle i}$ -suppercripted$$ 기호는 해당 벡터의 데카르트 성분을 나타낸다.null

단색파의 경우 이 표현은 다음과 같은 표현으로 변환할 수 있다.^[3]

${\displaystyle \mathbf{L} ={\frac {\epsilon _{0}{2i\omega }\sum _{i=x, z}\int \{E^{i}}^{\ast }\lt(\mathbf {r}\times \mathbf {\\nabla \} \} \la \} \rigla \rig) \right)E^{i}\오른쪽)d^{3}\mathbf {r} .}$

이 표현은 파동이 원통형 대칭이 아닐 때 일반적으로 비반복적이다.특히 양자 이론에서 개별 광자는 다음과 같은 OAM 값을 가질 수 있다.

${\displaystyle \mathbf {L} _{z}=m\hbar .}$

해당 파형 함수(OAM 연산자의 고유 기능)는 다음과 같은 일반적인 식을 갖는다.

${\displaystyle \langle \mathbf {r}m\rangele \propto e^{im\phi }}$

여기서 $\varphi {\displaystyle }$ ${\displaystyle \phi }$은(는) 원통형 좌표다.도입부에서 언급한 바와 같이, 이 표현은 광학적 소용돌이가 빔 축에 있는 나선파(위 그림 참조)를 갖는 파형에 해당한다.null

OAM 주의 생산

$l{\displaystyle }$=${\displaystyle }$± ${\displaystyle 1}$ ${\displaystyle l=\pm$ 1$}$의 궤도 각도 모멘텀 상태는 자연적으로 발생한다$$.^{[citation needed]}임의 $l{\displaystyle }$ ${\displaystyle l}$의 OAM 상태는 Spiral phase plate, Space light modulator 및 q-plate 등의 다양한 도구를 사용하여 인위적으로 생성될 수 있다$$.null

플라스틱이나 유리로 만들어진 나선파 판은 물질을 통과하는 빛에 위상 구배를 각인시키기 위해 물질의 두께가 나선형으로 증가하는 판이다.주어진 파장의 경우, 주어진 $l{\displaystyle }$ ${\displaystyle l}$의 OAM 상태에 따라$$ 스텝 높이(접시의 가장 얇은 부분과 ${\displaystyle \mathrm{가장}}$ 두꺼운 부분 사이의 높이)가 $s{\displaystyle }$= ${\displaystyle l}$ ${\displaystyle \lambda }$/${\displaystyle }$( ${\displaystyle \mathrm{n}}$- 1${\displaystyle }$) ${\displaystyle s=l\lambda /(n-1)$로 제공되어야 하며 $여기$서 n ${\displaystystyle$ n$}$은 정수다$$.파장 자체가 효율적이긴 하지만 상대적으로 생산 비용이 많이 들고 일반적으로 다른 파장에 맞춰 조절할 수 없는 것이 특징이다.^[4]null

빛의 위상을 수정하는 또 다른 방법은 회절 격자법을 사용하는 것이다.$l{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle l=0}$ 상태의$$ 경우 회절 그래팅은 평행선으로 구성된다.그러나 $l{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle l=1}$ 상태의$$ 경우 "fork" 탈구가 발생하며 탈구 위의 선 수는 아래보다 1개 더 많을 것이다. > {\$displaystyle l>1}$을(를) 가진 OAM 상태는 탈구 위와 아래의 라인 수의 차이를 증가시킴으로써 생성될 수 있다.^[5]나선파판과 마찬가지로 이러한 회절 그라프트는 $l{\displaystyle }$ ${\displaystyle l}$에$$대해 고정되지만 특정 파장에 제한되지는 않는다.null

공간 조명 조절기는 회절 만족도와 유사한 방식으로 작동하지만, 컴퓨터로 제어하여 광범위한 OAM 상태를 동적으로 발생시킬 수 있다.null

최근 진보

이 섹션은 대부분의 독자들이 이해하기에는 너무 기술적일 수 있다. 기술 세부 정보를 삭제하지 않고 비전문가가 이해할 수 있도록 개선하십시오.(2017년 7월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

이론적 연구는 일련의 광학적으로 구별되는 색소체가 흥분 상태를 지원할 수 있다는 것을 시사한다. 이러한 대칭은 흥분 이완 과정에서 0이 아닌 위상학적 전하의 방사선 모드가 직접 생성된다.^[6]null

가장 최근에는 OAM 세대를 위해 기하학적 위상 개념이 채택되었다.^[when?]기하학적 위상은 OAM ${\displaystyle {\mathrm{운반}}^{}}$ 파동의 ${\displaystyle {\mathrm{공간}}^{}}$ 위상 의존 계수(ei m { ${\$ e$^{im\phi }.$이와 같이 비등방성 분포를 이용하여 기하학적 위상을 도입한다.예를 들어, 회전 대칭 방식으로 분산된 선형 편광기로 구성된 메타 물질은 순서 1의 OAM을 생성한다.^[7]고차 OAM 파형을 생성하기 위해 스핀-오비트 커플링 효과를 낼 수 있는 나노 안테나를 설계한 후 위상 전하가 다른 메타수르면을 형성하도록 배열한다.^[8]따라서 전송되는 파동은 OAM을 전달하며, 그 순서는 위상 전하 값의 두 배가 된다.통상 전송형 메타서페이스의 경우 변환 효율이 높지 않다.높은 투과율을 달성하기 위한 대안적 해결책은 보완적(바비넷 반전) 메타서페이스 사용이다.^[9]반면 복합 PEC-PMC 메타서페이스와 같은 반사형 메타서페이스에서는 높은 변환 효율, 심지어 100% 효율을 달성하는 것이 훨씬 쉽다.^[10]null

통신에서의 잠재적 사용

OAM에 대한 연구는 광파를 통해 전례 없는 양의 데이터를 광섬유를 통해 운반할 수 있다는 것을 시사했다.예비 테스트에 따르면, 8개의 서로 다른 원형 극성으로 분할된 빛의 빔을 따라 이동하는 데이터 스트림은 초당 최대 2.5테라비트의 데이터 전송 용량(DVD 66개 또는 320기가바이트에 해당)을 입증했다.^[11]무선 및 mm 파장 주파수의 OAM 멀티플렉싱에 대한 추가 연구는 초당 32 기가비트의 데이터를 공중으로 전송할 수 있는 예비 테스트에서 입증되었다.^[12]이것이 MIMO와 같은 다른 계획 위에 어떤 용량을 추가할 것인지에 대한 논의가 진행 중이다.

빛의 궤도 각도 운동량 측정

빛의 스핀 각도 운동량(SAM)을 결정하는 것은 간단하다 – SAM은 빛의 양극화 상태와 관련이 있다. 즉, 광자당 AM은 각각 좌측 및 우측 원형 편광 빔에 있다.따라서 SAM은 파판(fave plate)을 이용하여 빛의 원형 양극화를 p- 또는 s-극화 상태로 변환한 다음 빛의 상태를 송신하거나 반영하는 편광 빔 스플리터를 사용하여 측정할 수 있다.^[4]null

그러나 빛의 궤도 각도 운동량(OAM) 측정을 위한 간단하고 신뢰할 수 있는 방법의 개발은 광 조작 분야에서 중요한 문제로 남아 있다.OAM(광자당)은 빔의 진폭 단면에서 발생하며 따라서 스핀 각도 운동량과 독립적이다. SAM은 직교 상태가 두 개뿐이지만 OAM은 정수 값 N을 취할 수 있는 상태로 설명된다.^[13]빛의 OAM 상태가 제한되지 않기 때문에 l의 정수 값은 다른 모든 값과 직교한다(독립).빔 스플리터가 SAM의 두 상태를 분리할 수 있는 경우, 어떤 장치도 OAM의 N(2보다 큰 경우) 모드를 분리할 수 없으며, 분명히 OAM 측정 문제를 최종적으로 해결하려면 모든 N 전위 상태를 완벽하게 검출해야 한다.그럼에도 불구하고 OAM 측정을 위한 몇 가지 방법이 조사되었다.null

나선형 프링 계산

OAM을 운반하는 빔은 나선상 구조를 가지고 있다.그러한 빔을 균일한 평면 파형으로 간섭하면 관측된 나선형 프링의 분석을 통해 입력 빔에 대한 위상 정보가 노출된다.마하-젠더 간섭계에서는 헬리컬 단계 소스 빔이 시준 경로를 따라 평면파 기준 빔을 방해하도록 만들어진다.간섭 프링크는 빔 허리의 평면 및/또는 레일리 레인지에서 관찰된다.이 프링들은 선원의 상대 위상 구조의 순수한 결과물이다.패턴의 각 가장자리는 한 단계부터 즉, 프링크를 세는 것으로 l의 값을 결정하는 데 충분하다.

확산 홀로그래픽 필터

컴퓨터로 생성된 홀로그램은 위상 특이점을 포함하는 빔을 생성하는 데 사용될 수 있으며, 이것들은 이제 OAM을 운반하는 빔의 생성을 위한 표준 도구가 되었다.이 생성 방법은 되돌릴 수 있다: 정해진 입구 개구부의 단일 모드 섬유와 결합된 홀로그램이 OAM의 필터가 된다.이 접근방식은 단일 포톤 수준에서 OAM 검출에 널리 사용된다.null

이러한 광학적 소자의 위상은 분해할 값 집합에서 선택한 위상학적 전하를 전달하는 몇 개의 포크-홀로그램의 중첩이 된다.원거리 채널의 위치는 각 포크-홀로그램 기여도를 해당 공간 주파수 반송파에 곱하여 제어할 수 있다.^[14]null

기타 방법

빛의 OAM을 측정하는 다른 방법으로는 회전 도플러 효과, 도브 프리즘 간섭계에 기초한 시스템,^[15] 갇힌 입자의 스핀 측정, 개구부로부터의 회절 효과 연구, 광학적 변환 등이 있다.^[16][17]후자는 OAM 모드의 각도 위상 패턴을 푸리에 공간에서 후속적으로 해결할 수 있는 평면파 위상 패턴으로 풀기 위해 확산 광학 소자를 사용한다.그러한 체계의 분해능은 출력 스트립 모양의 모드의 위상 범위를 입력 빔 폭의 나선 수로 확장하는 나선 변환에 의해 개선될 수 있다.^[18]null

양자 정보 응용 프로그램

OAM 상태는 일관성 있는 초상으로 생성될 수 있고 그것들은 뒤얽힐 수 있는데,^[19][20] 이것은 양자 정보 프로토콜에 대한 계획의 필수적인 요소다.이러한 상태는 파라메트릭 다운-변환 및 공간 조명 변조기(SLM)를 사용하여 측정한 상관 관계를 사용하여 생성할 수 있다.^[21]

Qudit(쿼빗의 2단계와는 반대로 d레벨이 있는)을 사용하면 양자 키 분배 체계의 견고성을 개선할 수 있는 것으로 나타났다.OAM 상태는 그러한 시스템의 적절한 물리적 실현을 제공하며, 원칙 증명 실험($l{\displaystyle }$=${\displaystyle }$- ${\displaystyle 3}$ ${\displaystyle l=-3}$ ~ l$$${\displaystyle }$= ${\displaystyle 3}$ ${\displaystyle l=$^[22]3})이 입증되었다.null

전파천문학

2019년 왕립천문학회 월간고시에 게재된 서한에는 OAM 전파신호가 5천만 광년 이상 떨어진 M87* 블랙홀 부근에서 수신되었다는 증거가 제시되어 광학 각운동량 정보가 천문학적 거리에 걸쳐 전파될 수 있음을 시사했다.^[23]null

참고 항목

참조

외부 링크

위키미디어 커먼스는 파동의 궤도 각도 운동량과 관련된 미디어를 보유하고 있다.

• 포리텍
• Allen, L.; Barnett, Stephen M. & Padgett, Miles J. (2003). Optical Angular Momentum. Bristol: Institute of Physics. ISBN 978-0-7503-0901-1..
• Torres, Juan P. & Torner, Lluis (2011). Twisted Photons: Applications of Light with Orbital Angular Momentum. Bristol: Wiley-VCH. ISBN 978-3-527-40907-5..
• Andrews, David L. & Babiker, Mohamed (2012). The Angular Momentum of Light. Cambridge: Cambridge University Press. p. 448. ISBN 9781107006348.

• 글래스고 광학 그룹
• 레이든 물리학 연구소
• ICFO
• 유니버시아드 디 나폴리 "페데리코 2세"
• 우니베르시타 디로마 "라 사피엔자"
• 오타와 대학교
• 레이저 포인터를 사용한 기본 데모