팔각형 피라미드

팔각형 피라미드
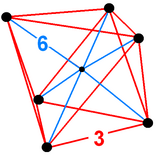
슐레겔 도표
유형	다면 피라미드
슐레플리 기호	( ) ∨ {3,4} ( ) ∨ r{3,3} ( ) ∨ s{2,6} ( ) ∨ [{4} + { }] ( ) ∨ [{ } + { } + { }]
세포	9	1 {3,4} 8 ( ) ∨ {3}
얼굴	20 {3}
가장자리	18
정점	7
이중	입방피라미드
대칭군	B3, [4,3,1], 주문 48 [3,3,1], 주문 24 [2+,6,1], 주문 12 [4,2,1], 주문 16 [2,2,1], 주문 8
특성.	볼록한, 정면의

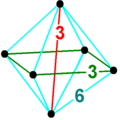
4차원 기하학에서 팔면 피라미드는 밑면에 팔면체 1개와 정점에서 만나는 8개의 삼각형 피라미드 세포로 경계를 이루고 있다.팔면체는 가장자리 길이로 나누어진 곡선을 가지고 있기 때문에,^[1] 삼각형 피라미드는 적당한 높이를 계산함으로써 (일반적인 사면체로서) 일반 얼굴로 만들 수 있다.

팔면 피라미드의 발생

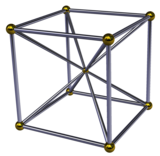
일반 16세포는 모든 꼭지점 주위에 팔면 피라미드가 있으며, 팔면체는 16세포의 중심을 통과한다.따라서 두 개의 일반적인 팔면 피라미드 기지를 베이스에 배치하는 것은 16개의 셀을 구성한다.16셀 테셀러는 4차원 공간을 16셀 허니콤으로 표현한다.

정확히 24개의 정규 팔면 피라미드가 4차원 공간(각 피라미드의 꼭지점)의 꼭지점 주위로 함께 들어맞을 것이다.이 구조는 중앙 꼭지점을 24개의 가장자리 길이의 긴 반지름으로 둘러싸인 8각형 경계 셀을 가진 24개의 셀을 산출한다.단위 에지 길이 24셀의 4차원 함량은 2이므로 일반 팔면 피라미드의 함량은 1/12이다.24셀 테셀러는 4차원 공간을 24셀 벌집처럼 만든다.

팔각형 피라미드는 잘린 5정맥의 꼭지점이다.

팔면 피라미드의 그래프는 평면 표지를 가진 연결된 그래프 자체가 투영 평면이라는 네가미의 추측에 대한 가능한 최소의 표본이다.^[2]

기타다각질

입방피라미드

팔면 피라미드의 이중은 입방피라미드로, 입방피라미드와 6개의 사각피라미드가 정점에서 만나는 것으로 보인다.

사각피라미달 피라미드

사각피라미달 피라미드
슐레겔 도표
유형	다면 피라미드
슐레플리 기호	( ) ∨ [( ) ∨ {4}] [( )∨( )] ∨ {4} = { } ∨ {4} { } ∨ [{ } × { }] { } ∨ [{ } + { }]
세포	6	2 { } ∨ {4} 4 { } ∨ {3}
얼굴	12 {3} 1 {4}
가장자리	13
정점	6
이중	셀프듀얼
대칭군	[4,1,1], 주문 8 [4,2,1], 주문 16 [2,2,1], 주문 8
특성.	볼록한, 정면의

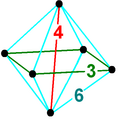
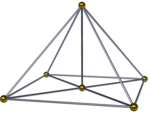
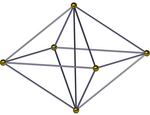
사각형 피라미달 피라미드, ( ) ∨ [( ) ∨ {4})는 이등분된 팔면 피라미드다.그것은 정사각형의 피라미드 기지와 4개의 사면체 그리고 정점에서 또 하나의 정사각형의 피라미드 미팅을 더 가지고 있다.가장자리 중심의 투영법에서도 공통 가장자리를 감싸고 있는 네 개의 사면체(四面體)가 있는 네모난 비피라미드로 볼 수 있다.두 개의 꼭지점의 높이가 같을 경우 보다 높은 대칭 이름 [( ) ∨ ( ) ∨ ( ) ∨] ∨ {4} = { ∨} ∨ {4}을(를) 부여할 수 있으며, 가장자리는 수직 정사각형에 연결된다.^[3]

사각피라미드 피라미드는 직사각피라미드 피라미드, { } ∨[{} × { }] 또는 롬비크피라미드 피라미드, { ∨[{} + {}], 또는 다른 하부 대칭 형태로 변형될 수 있다.

정사각형 모양의 피라미드는 5개의 직립형, 3개의 직립형 벌집형 등을 포함한 형태의 균일한 폴리탑에 꼭지점으로 존재한다.

참조

외부 링크

• Olshevsky, George. "Pyramid". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Klitzing, Richard. "4D Segmentotopes".
  • Klitzing, Richard. "Segmentotope octpy, K-4.3".
• Richard Klitzing, 균일한 다면체의 축대칭 모서리 면