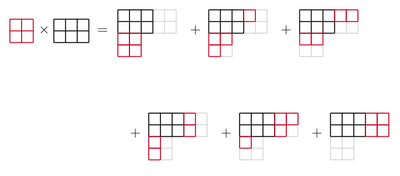
리틀우드-리처드슨 규칙

수학에서 리틀우드-리처드슨 규칙은 다른 슈르 함수의 선형 결합으로 두 슈르 함수의 제품을 분해할 때 발생하는 계수에 대한 조합적 설명이다.이 계수들은 자연수로서, 리틀우드-리처드슨 법칙은 어떤 꼬치형 표를 세는 것이라고 설명한다.그것들은 다른 많은 수학적인 맥락에서 발생하는데, 예를 들어, 일반 선형 집단의 유한차원 표현물의 텐서 생산물의 분해 또는 대칭 집단의 표현 이론에서 특정 유도 표현물의 분해 또는 Y를 다루는 대수적 결합론의 영역에서 발생한다.ung tableaux 및 대칭 다항식.

리틀우드-리처드슨 계수는 세 개의 파티션(예: $\lambda ,\mu ,\nu$ , $\lambda ,\mu ,\nu$ , $\lambda ,\mu ,\nu$ μ , $\lambda ,\mu ,\nu$ \ $displaystyle$ $\lambda$ $,\mu ,\nu$ $})$ 에 따라 달라지는데 $\lambda ,\mu ,\nu$ 이 중 $\nu$ ${\displaystyle \nu$ $}$ 과 $\lambda$ $\mu$ $\mu$ ${\$ displaystate \nu $}$ 은 sch 기능을 제공하며 $\nu$ , line in line.귀의 $c_{\lambda ,\mu }^{\nu }$ 조합; 즉, $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ , $c_{\lambda ,\mu }^{\nu }$ μ $c_{\lambda ,\mu }^{\nu }$ {\ $displaystyle c_{\dada$ ,\ $mu$ ^{\ $nu }}}.$

s_{\putda }s_{\mu }=\sum _{\nu }c_{\putda,\mu ^{\nu }}

리틀우드-리처드슨 규칙은 $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ , $\nu /\lambda$ $c_{\lambda ,\mu }^{\nu }$ ${\$ 는 $c_{{\lambda ,\mu }}^{\nu }$ $\nu /\lambda$ $\mu$ / $\nu /\lambda$ ${\$ displaysty \ $nu$ $/\lambda$ $}$ 의 리틀우드-리처드 \ $mu$ 테이블a $.$

역사

불행히도 리틀우드-리처드슨 통치는 처음에 의심되었던 것보다 훨씬 증명하기가 어렵다.저자는 리틀우드-리처드슨 통치가 사람들을 달에 착륙시키는 데 도움을 주었지만, 그들이 달에 도착한 후에야 증명되었다고 들은 적이 있다.

Gordon James (1987)

리틀우드-리처드슨 규칙은 D. E. 리틀우드와 A. R. 리처드슨(1934, 정리 III 페이지 119)에 의해 처음 명기되었지만, 그들은 정리라고 주장했지만, 몇몇 아주 간단한 특수한 경우에서만 그것을 증명했다.로빈슨(1938년)은 그들의 증거를 완성한다고 주장했지만, 그의 주장은 너무나 불명확하게 씌어 있어서 한동안 이러한 공백이 눈에 띄지 않았고, 그의 주장은 책(리틀우드 1950년)에 그대로 재현되어 있다.그 틈의 일부는 나중에 맥도날드(1995)가 채웠다.이 규칙의 첫 번째 엄격한 증거는 C에 의해 필요한 결합 이론이 개발된 후 슈첸베르거(1977년)와 토마스(1974년)에 의해 발견된 40년 후에 주어졌다. 스헨스테드(1961년), 슈첸베르거(1963년), 크누스(1970년 ) 등이 로빈슨-스헨스테드 통신에 관한 연구로 나왔다.이제 (Gasharov 1998), 벤더-크누스의 비자발성을 이용한 (Steambridge 2002)과 같은 몇 가지 짧은 규칙의 증거가 있다.Littelmann(1994)은 Littelmann 경로 모델을 사용하여 Littelmann-Richardson 규칙을 다른 semisimple Lie 그룹에 일반화했다.

리틀우드-리처드슨 규칙은 완전하고 공개된 증거 이전에 나타난 오류의 수로 악명이 높다.그것이 불완전하다는 것을 증명하기 위한 몇 번의 출판된 시도들이 있고, 그것을 가지고 손 계산을 할 때 특히 오류를 피하기는 어렵다: D. E. 리틀우드와 A. R. 리처드슨(1934)의 원본 예조차도 오류를 포함하고 있다.

리틀우드-리처드슨 테이블로

리틀우드-리처드슨 테이블라우

리틀우드-리처드슨 테이블라우(Littlewood-Richardson tableau)는 반전된 행을 연결하여 얻은 시퀀스가 격자어(또는 격자 순열)라는 추가 속성이 있는 스큐 세미산다드 테이블라우로, 이는 시퀀스의 모든 초기 부분에서 숫자 $i$ ${\$ $displaysty$ i $}$ 가 적어도 숫자 $i+1$ 만큼 자주 $i$ 발생한다는 것을 의미한다. $aystyle i+1$ } $.$ 또 다른 등가 특성화(분명히 그렇지는 않지만)는 표고 자체와 표고에서 가장 왼쪽 열을 몇 개 제거하여 얻은 표고 자체에서 무게가 약하게 감소한다는 것이다.많은 다른 결합 개념들이 리틀우드-리처드슨 테이블로 편향되어 있는 것으로 밝혀졌으며, 따라서 리틀우드-리처드슨 계수를 정의하는 데도 사용될 수 있다.

또 다른 리틀우드-리처드슨 테이블라우

예

Consider the case that $\lambda =(2,1)$ , $\mu =(3,2,1)$ and $\nu =(4,3,2)$ . Then the fact that $c_{\lambda ,\mu }^{\nu }=2$ can be deduced from the fact that the two tableaux shown at the right는 모양 $\nu /\lambda$ / $\nu /\lambda$ { $\nu /\lambda$ \ $displaystyle \nu /\lambda }$ 과 무게 $\nu /\lambda$ $\mu$ ${\\displaystyle \mu }$ 의 유일한 리틀우드-리처드슨 테이블이다 $\mu$ 실제로 스큐 다이어그램의 첫 번째 비어 있지 않은 행의 마지막 상자는 항목 1만 포함할 수 있으므로, 첫 번째 줄 전체는 1로 채워져야 한다(이는 모든 리틀우드 리틀우드 리틀우드 리틀우드-리처드-리처드-리처드 리차 탭의 경우 사실이다.leau); 두 번째 행의 마지막 상자에 2 by column 엄격성과 격자 단어가 2를 포함하기 전에 더 큰 항목을 포함할 수 없다는 사실만 넣을 수 있다.두 번째 행의 첫 번째 상자는 이제 1 또는 2를 사용할 수 있다.일단 그 항목이 선택되면, 세 번째 행은 몸무게(3,2,1)를 약하게 증가시키는 순서로 만들기 위해 나머지 항목을 포함해야 하므로, 우리는 더 이상 선택의 여지가 없다. 두 경우 모두 리틀우드-리처드슨 테이블라우를 찾는 것으로 드러난다.

더 기하학적 설명

표고에서 다소 특이한 순서로 읽혀지는 입력 순서가 격자어를 형성하는 조건은 보다 국소적이고 기하학적인 조건으로 대체될 수 있다.세미스탠다드 테이블라우에서는 동일한 열에 절대 동일한 항목이 발생하지 않기 때문에, 오른쪽에서 왼쪽으로 어떤 값의 복사본에 번호를 매길 수 있으며, 이것은 격자어가 되어야 하는 순서에서 발생 순서다.각 항목의 인덱스와 관련된 번호로 전화를 걸어 인덱스 j를 i[j]로 입력하십시오.이제 일부 리틀우드-리처드슨 테이블au에 인덱스 j가 $i>1$ 있는 $i>1$ i > 1 ${\$ $displaystyle$ $i>1}$ 이(가) 포함되어 있는 경우, 해당 항목 i $[j$ ]는 $i$ - 1 $(i-1)[j]$ ) $(i-1)[j]$ [ $(i-1)[j]$ 의 항목보다 엄격히 아래 행에 발생해야 하며, $(i-1)[j]$ 이 역시 항목 i - 1은 항목 i만큼 자주 발생하기 때문에 확실히 발생한다.사실 항목 i[j]도 같은 항목 $(i-1)[j]$ - $(i-1)[j]$ ) $(i-1)[j]$ [ $(i-1)[j]$ $(i-1)[j]$ ${\displaystyle (i-1)[j]}($ 첫눈에 더 엄격한 조건인 것 같음)보다 더 이상 오른쪽에 있지 않은 열에서 발생해야 한다.만약 리틀우드-리처드슨 테이블라우의 무게가 사전에 고정되어 있다면, 그 다음에 색인화된 항목들의 고정된 컬렉션을 형성할 수 있고, 만약 그것들이 세미산다드 테이블로의 그것들 그리고 동일한 항목의 색인화된 복사본들이 t의 오른쪽에서 왼쪽 순서를 존중해야 하는 조건들 외에, 이것들이 그러한 기하학적 제약들을 존중하는 방식으로 놓여진다면.지수, 그 결과의 tableaux는 Littlewood-Richardson tableaux가 보장된다.

규칙의 알고리즘 형식

위에서 설명한 리틀우드-리처드슨은 개별 리틀우드-리처드슨 계수에 대한 조합적 표현을 제공하지만, 이러한 계수의 값을 찾기 위해 리틀우드-리처드슨 표의 열거에 대한 실질적인 방법은 표시하지 않는다.실제로 $\lambda ,\mu ,\nu$ $\lambda ,\mu ,\nu$ , μ , $\lambda ,\mu ,\nu$ , $\lambda ,\mu ,\nu$ {\ $displaystyle \lambda$ ,\ $mu$ ,\ $nu}$ 형태 $\nu /\lambda$ / $\nu /\lambda$ ${\displaysty \lambda$ $\mu$ } 및 중량 $\nu /\lambda$ $\mu$ ${\\displaysty \mu$ }의 리틀우드-리처드슨 테이블이 존재하는지 $\mu$ 여부를 판단할 수 있는 간단한 기준은 없다 $\lambda ,\mu ,\nu$ (여러 가지 필요조건은 없다). $|\lambda |+|\mu |=|\nu |$ + $|\lambda |+|\mu |=|\nu |$ = $|\lambda |+|\mu |=|\nu |$ $displaystyle \lambda$ + $\mu$ = $\nu }$ $|\lambda |+|\mu |=|\nu |$ ) 따라서 어떤 경우에는 치밀한 검색을 거쳐야 하지만, 다만 해결책이 존재하지 않는다는 것을 발견하는 것은 불가피해 보인다.

그럼에도 불구하고 이 규칙은 슈르 함수의 산물의 완전한 분해, 즉 고정된 and과 μ에 $c_{\lambda ,\mu }^{\nu }$ 대한 모든 $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ , $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ {\ $displaystyle c_{\lambda$ ,\ $mu }^{\nu }}}}$ 를 결정하는 상당히 효율적인 절차로 이어진다.이렇게 하면 리틀우드-리처드슨 테이블보의 중량이 고정되고 그 모양의 "내부 부분" λ이 고정되지만, "외부 부분" free은 자유로워진다.가중치를 알 수 있기 때문에 기하학적 설명에 있는 인덱스된 항목 집합이 고정된다.이제 연속 인덱싱된 항목의 경우 기하학적 제약에 의해 허용되는 모든 위치를 역추적 검색에서 시도할 수 있다.출품작은 증가 순서에 따라 시도할 수 있으며, 동일한 출품작 중에서는 지수를 감소시켜 출품작을 시도할 수 있다.후자의 지점은 검색 절차의 효율성의 핵심이다. 즉, 항목 i[j $i[j+1]$ 는 i $i[j+1]$ [ $i[j+1]$ + $i[j+1]$ 1 $]$ {\ $displaystyle i[j+$ 1 $i[j+1]$ 의 오른쪽에 있는 열로 $i-1[j]$ 되지만 $i-1[j]$ $i-1[j]$ - $i-1[j]$ [ $i-1[j]$ j $]$ {\ $displaystyle$ i-1 $[$ ]보다 더 이상 오른쪽에 있지 않다.이것은 가능한 위치의 집합을 강력하게 제한하지만, 항상 $i[j]$ [ $i[j]$ $i[j]$ ${\displaystyle$ i $[j]}$ 에 대해 적어도 하나의 유효한 위치를 남겨두기 때문에 $i[j]$ 모든 항목 배치 시 적어도 하나의 완전한 리틀우드-리처드슨 테이블라우가 생성될 것이며, 검색 트리는 막다른 곳을 포함하지 않는다.

고정 λ 및 ν에 대한 $c_{\lambda ,\mu }^{\nu }$ 모든 계수 $c_{\lambda ,\mu }^{\nu }$ $c_{\lambda ,\mu }^{\nu }$ , $c_{\lambda ,\mu }^{\nu }$ μ $c_{\lambda ,\mu }^{\nu }$ ${\$ 을(를) 찾는데 유사한 방법을 사용할 수 있지만 μ는 변화한다.

리틀우드-리처드슨 계수

리틀우드-리처드슨 계수 c는^ν
_λμ 다음과 같은 상호 관련 방식으로 나타난다.

그것들은 Schur 함수의 기초와 관련하여 대칭함수의 링에 있는 제품의 구조 상수다.

s_{\buda }s_{\mu }=\sum c_{\buda \mu }^{\nu }s_{\nu }}}}}}

또는 동등하게 c는^ν
_λμ s와_ν ss의_λ_μ 내적 산물이다.

스큐 슈르 함수를 슈르 함수로 표현한다.

s_{\nu /\sumda }=\sum _{\mu }c_{\nu }^{\nu }s_{\mu }}}

c는^ν
_λμ Grassmannian에서 교차로 번호로 나타난다.

\probma _{\mu }=\\mu }=\sum c_{\mu \nu _{\nu _}}}

여기서 σ은_μ μ에 해당하는 그라스만족의 슈베르트 품종이다.

c는^ν
_λμ 대칭군 곱의_λ V_λ ⊗ V가_μ_μ S에서_ν S × S까지의_λ_μ 표현 V의_ν 제한에 나타나는 횟수로, 프로베니우스 상호주의에 의해 V_λ ⊗ V에서_μ 유도된 S의_ν 표현에 V가 발생하는_ν 횟수도 된다.
c는^ν
_λμ 두 Schur 모듈의 텐서 제품(Fulton 1997) 분해에 나타난다(특정 선형 그룹의 불확실한 표현).

E^{\lambda }\otimes E^{\mu }=\bigoplus _{\nu }^{\oplus c_{\lambda \mu }^{}}}.

c는^ν
_λμ 일부 고정된 표준형 λ의 Young tableau에 해당하는 de/μ 형상의 표준 Young tableau의 수이다.
c는^ν
_λμ ν/λ 형상의 리틀우드-리처드슨 테이블aux와 중량 μ의 수입니다.
c는^ν
_λμ μ와 μ/μs 사이의 그림 수입니다.

특례

피에리의 공식

칸막이 중 하나가 한 부분만 가지고 있는 경우의 리틀우드-리처드슨 지배의 특수한 경우인 피에리의 공식은 다음과 같이 말하고 있다.

S_{\mu }S_{n}=\sum _{\lambda }S_{\lambda }}}}}

여기서 S는_n 한 행의 칸막이의 Schur 함수로서, 합계는 모든 칸막이에 걸쳐 있다 μ에서 얻은 모든 칸막이에 대해 동일한 열에 두 개의 요소가 없다.

직사각형 파티션

두 칸막이 모두 직사각형 모양이면, 합도 무중복이다(Okada 1998).a, b, p 및 q 양의 정수를 p $(a^{p})$ $\geq$ $\geq$ $\geq$ 로 $\geq$ 수정. $(a^{p})$ ) {\ $displaystyle (a^{p})}$ 파티션의 $(a^{p})$ 길이를 a의 p 부분으로 표시하십시오. $s_{(a^{p})}s_{(b^{q})}$ ( $s_{(a^{p})}s_{(b^{q})}$ ) $s_{(a^{p})}s_{(b^{q})}$ ( $s_{(a^{p})}s_{(b^{q})}$ )s (bq $){\$ p} $s_$ {( $a^{p}$ s_ ${(b^{q}}}}}}}}$ 의 비경쟁적 구성 요소를 인덱싱하는 파티션은 $\leq p+q$ 길이가 $\leq p+q$ $\leq p+q$ + $\leq p+q$ 인 $\lambda$ $\lambda$ $\displaystyle \lambda$ $}}$ 이다 $s_{{(a^{p})}}s_{{(b^{q})}}$ $.$

$\possda _{q+1}=\podda _\p}=a,$
$\bda _{q}\geq \mathrm {max}(a,b)$
$\i}+\putda _{p+q-i+1}=a+b,\pair {i=1,\pair,q}$

예를 들어,

.

일반화

대칭 그룹의 크로네커 계수 감소

The reduced Kronecker coefficient of the symmetric group ${\bar {C}}_{\lambda ,\mu ,\nu }$ is a generalization of $c_{\lambda ,\mu }^{\nu }$ to three arbitrary Young diagrams $\lambda ,\mu ,\nu$ , which is symmetric under permutations3개의 도표 중에서

스큐 슈르 함수

젤레빈스키(1981)는 리틀우드-리처드슨 규칙을 확장하여 슈르 기능을 다음과 같이 왜곡시켰다.

{\displaystyle s_{\lambda }s_{\mu /\nu }=\sum _\lambda +\omega(T_{\geq j})\in P}s_{\lambda +\omega(T)}}).

여기서 합계가 μ/μs의 모든 테이블aux T 위에 있으므로, 모든 j에 대해 정수 sequence+Ω(T_≥j)의 순서는 증가하지 않으며, Ω은 중량이다.

뉴웰-리틀우드 수

뉴웰-리틀우드 숫자는 입방식에^[1] 의해 리틀우드-리처드슨 계수에서 정의된다.

{\displaystyle N_{\mu ,\nu ,\lambda }=\sum _{\no,\beta,\gamma }c_{\no,\lambda }}}=\sum }c_{\no,\lambda }}}}}}}}}}}}}}}}}}}}}}}}}}sa

Newell-Littlewood 번호는 유형 $B,$ $, D$ 의 고전적 $Lie$ 그룹의 유한차원 표현에 대한 텐서 곱의 일부를 제공한다 $B,C,D$

영 다이어그램 크기 $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ , $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ 0 $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ + $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ μ = $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ = $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ $style$ { $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ { $c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |$ μ { { { { { $\lambda ,\mu }^{\nu }^{\$ nu \neq \ $lambda + \nu$ = $\nu$ \nu $}.$

N_{\mu ,\nu ,\lambda }\neq 0\implies \left\{\begin{array}{l}}{l}}\lambda + \mu \nu \in 2\mathb {Z}\end}오른쪽.

뉴웰-리틀우드 번호는 다음과 같은 의미에서 리틀우드-리처드슨 계수의 일반화다.

\mu + \nu = \lambda \implies N_{\mu ,\nu }=c_{\mu ,}^{\lambda }}}}}}}

Newell-Littlewood numbers that involve a Young diagram with only one row obey a Pieri-type rule: $N_{(k),\mu ,\nu }$ is the number of ways to remove ${\frac {k+ \mu - \nu }{2}}$ boxes from $\mu$ (from different columns), then $\nu$ - ${\frac {k-|\mu |+|\nu |}{2}}$ + ${\frac {k-|\mu |+|\nu |}{2}}$ ${\frac {k-|\mu |+|\nu |}{2}}$ ${\$ + $\nu }{2$ }}상자 ${\frac {k-|\mu |+|\nu |}{2}}$ (다른 열에)를 추가하여 $\nu }$ 을 $\nu$ ^[1]를) 만드십시오.

뉴웰-리틀우드 번호는 기본 원소가 파티션인 연관성 및 정류 대수의 구조 상수로, 제품 $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ = $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ N $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ ν, $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ , $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ , λ, $\displaystyle \time \nu =\sum \\\\\lambda },$ 예를 들면 $\mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda$ .

(1)\time (k)=(k-1)+(k+1)+(k,1)\quad {\text{(뉴웰-리틀우드)}}

{\displaystyle(1)\time(k)=(k+1)+(k,1)\quad {\text{(리틀우드-리처드슨)}}}

예

아래의 리틀우드-리처드슨 계수의 예는 파티션 partitions에 의해 색인화된 슈르 다항식 S의_π 제품 측면에서 제시되며, 공식은 다음과 같다.

S_{\lambda }S_{\lambda }=\sum c_{\lambda \mu }^{}\nu }}

최대 4의 ν을 갖는 모든 계수는 다음을 통해 주어진다.

SS₀_π = S_π, 여기서 S₀=1은 빈 파티션의 Schur 다항식이다.
제곱합₁₁₂ = S + S₁₁
제곱합₂₁₃ = S + S₂₁
제곱합₁₁₁₁₁₁ = S + S₂₁
제곱합₃₁₄ = S + S₃₁
S₂₁S₁ = S₃₁ + S₂₂ + S₂₁₁
S₂S₂ = S₄ + S₃₁ + S₂₂
제곱합₂₁₁₃₁ = S + S₂₁₁
제곱합₁₁₁₁₁₁₁₁ = S + S₂₁₁
S₁₁S₁₁ = S₁₁₁₁ + S₂₁₁ + S₂₂

작은 칸막이에 대한 계수의 대부분은 0 또는 1이며, 특히 피에리의_n 공식과 그 전치된 상대 때문에 S 또는_11...1 S 형태의 요인 중 하나가 될 때마다 발생한다.계수가 1보다 큰 가장 간단한 예는 두 요인 중 어느 것도 이러한 형태를 가지지 않을 때 발생한다.

SS₂₁₂₁ = S₄₂ + S₄₁₁ + S₃₃ + S + 2S₃₂₁ + S₃₁₁₁₂₂₂ + S + S₂₂₁₁.

큰 파티션의 경우 계수가 더 복잡해진다.예를 들어,

S321S321)S642 +S6411 +S633 +2S6321 +S63111 +S6222 +S62211 +S552 +S5511 +2S543 +4S5421 +2S54111 +3S5331 +3S5322 +4S53211 +S531111 +2S52221 +S522111 +S444 +3S4431 +2S4422 +3S44211 +S441111 +3S4332 +3S43311 +4S43221 +2S432111 +S42222 +S422211 +S3333 34면과 전체적인 다양한 62과 +2S33321 +S333111 +S33222 +S332211가 가장 큰 coeffic.ient 4
SS는₄₃₂₁₄₃₂₁ 206개의 항을 합한 것이며, 총복수는 930이며, 가장 큰 계수는 18이다.
SS는₅₄₃₂₁₅₄₃₂₁ 총복수 26704의 1433항 합계로, 가장 큰 계수(S의_86543211 계수)는 176이다.
SS는₆₅₄₃₂₁₆₅₄₃₂₁ 10873 항을 합한 것이며, 총 다중성은 1458444(그래서 계수의 평균값이 100 이상이며, 2064년까지 클 수 있다).

리틀우드&리차드슨(1934, 페이지 122-124)이 제시한 원래 예는 (3개의 표에 대해 정정했으나 최종 합계에 포함시키는 것을 잊어버렸다)이다.

SS₄₃₁₂₂₁ = S₆₅₂ + S + S₆₅₁₁₆₄₂₁ + S₆₄₃ + S₆₄₁₁₁ + S₆₃₃₁ + S₆₃₂₂₆₃₂₁₁ + S + S₅₅₃ + S + S₅₅₂₁ + S + 2S₅₅₁₁₁ + 2S₅₄₃₁₅₄₂₂₅₄₂₁₁ + 2S + 3S + S + S₅₄₁₁₁₁₅₃₃₂₅₃₃₁₁ + S₅₃₂₂₁₅₃₂₁₁₁ + S + S₄₄₃₂ + S + S₄₄₃₁₁ + S + S + S + S₄₄₂₂₁ + S₄₄₂₁₁₁₄₃₃₂₁ + S + S + S + S + S + S + S + S + S + S + S + S + S + S₄₃₂₂₂ + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S + S₄₃₂₂₁₁ + S +

다음 34개 표에서 26개 항:

....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11     ...22  ...22  ...2   ...2   ...2   ...2   ...    ...    ... .3     .      .23    .2     .3     .      .22    .2     .2             3             3      2      2      3      23     2                                          3                    3  ....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1    ...12  ...12  ...12  ...12  ...1   ...1   ...1   ...2   ...1 .23    .2     .3     .      .23    .22    .2     .1     .2              3      2      2      2      3      23     23     2                      3                                  3  ....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1    ...2   ...2   ...2...    ...    ...    ...    ...     .1     .3     .      .12    .12    .1     .2     .2       2      1      1      23     2      22     13     1 3      2      2             3      3      2      2               3                                  3  ....   ....   ....   ....   ....   ....   ....   ....    ...1   ...1   ...1   ...1   ...1   ...    ...    ...     .12    .12    .1     .2     .2     .11    .1     .1       23     2      22     13     1      22     12     12        3      3      2      2      3      23     2                             3                    3

스큐 슈르 함수를 계산하는 것도 비슷하다.예를 들어 ν=5432 및 λ=331에 대한 15개의 리틀우드-리처드슨 테이블aux는 다음과 같다.

...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2 .11   .11   .11   .12   .11   .12   .13   .13   .23   .13   .13   .12   .12   .23   .23 12    13    22    12    23    13    12    24    14    14    22    23    33    1334

S_5432/331 = =c₅₂ S_μ = S + S₅₁₁₄₁₁₁ + S + S₂₂₂₁ + 2S₄₃ + 2S₃₂₁₁ + 2S₃₂₂ + 2S + 2S₃₃₁ + 3S₄₂₁ (Fulton 1997, 페이지 64)

메모들

^ ^a ^b Gao, Shiliang; Orelowitz, Gidon; Yong, Alexander (2021). "Newell-Littlewood numbers". Trans. Amer. Math. Soc. 374 (9): 6331–6366. arXiv:2005.09012v1. doi:10.1090/tran/8375. S2CID 218684561.

참조

Fulton, William (1997), Young tableaux, London Mathematical Society Student Texts, vol. 35, Cambridge University Press, p. 121, ISBN 978-0-521-56144-0, MR 1464693
Gasharov, Vesselin (1998), "A short proof of the Littlewood-Richardson rule", European Journal of Combinatorics, 19 (4): 451–453, doi:10.1006/eujc.1998.0212, ISSN 0195-6698, MR 1630540
James, Gordon (1987), "The representation theory of the symmetric groups", The Arcata Conference on Representations of Finite Groups (Arcata, Calif., 1986), Proc. Sympos. Pure Math., vol. 47, Providence, R.I.: American Mathematical Society, pp. 111–126, MR 0933355
Knuth, Donald E. (1970), "Permutations, matrices, and generalized Young tableaux", Pacific Journal of Mathematics, 34 (3): 709–727, doi:10.2140/pjm.1970.34.709, ISSN 0030-8730, MR 0272654
Littelmann, Peter (1994), "A Littlewood-Richardson rule for symmetrizable Kac-Moody algebras" (PDF), Invent. Math., 116: 329–346, Bibcode:1994InMat.116..329L, doi:10.1007/BF01231564, S2CID 85546837
Littlewood, Dudley E. (1950), The theory of group characters and matrix representations of groups, AMS Chelsea Publishing, Providence, RI, ISBN 978-0-8218-4067-2, MR 0002127
Littlewood, D. E.; Richardson, A. R. (1934), "Group Characters and Algebra", Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, The Royal Society, 233 (721–730): 99–141, Bibcode:1934RSPTA.233...99L, doi:10.1098/rsta.1934.0015, ISSN 0264-3952, JSTOR 91293
Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR 1354144, archived from the original on 2012-12-11
Okada, Soichi (1998), "Applications of minor summation formulas to rectangular-shaped representations of classical groups", Journal of Algebra, 205 (2): 337–367, doi:10.1006/jabr.1997.7408, ISSN 0021-8693, MR 1632816
Robinson, G. de B. (1938), "On the Representations of the Symmetric Group", American Journal of Mathematics, The Johns Hopkins University Press, 60 (3): 745–760, doi:10.2307/2371609, ISSN 0002-9327, JSTOR 2371609 즈블 0019.25102
Schensted, C. (1961), "Longest increasing and decreasing subsequences", Canadian Journal of Mathematics, 13: 179–191, doi:10.4153/CJM-1961-015-3, ISSN 0008-414X, MR 0121305
Schützenberger, M. P. (1963), "Quelques remarques sur une construction de Schensted", Mathematica Scandinavica, 12: 117–128, doi:10.7146/math.scand.a-10676, ISSN 0025-5521, MR 0190017
Schützenberger, Marcel-Paul (1977), "La correspondance de Robinson", Combinatoire et représentation du groupe symétrique (Actes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Strasbourg, 1976), Lecture Notes in Mathematics, vol. 579, Berlin, New York: Springer-Verlag, pp. 59–113, doi:10.1007/BFb0090012, ISBN 978-3-540-08143-2, MR 0498826
Stembridge, John R. (2002), "A concise proof of the Littlewood-Richardson rule" (PDF), Electronic Journal of Combinatorics, 9 (1): Note 5, 4 pp. (electronic), doi:10.37236/1666, ISSN 1077-8926, MR 1912814
Thomas, Glânffrwd P. (1974), Baxter algebras and Schur functions, Ph.D. Thesis, Swansea: University College of Swansea
van Leeuwen, Marc A. A. (2001), "The Littlewood-Richardson rule, and related combinatorics" (PDF), Interaction of combinatorics and representation theory, MSJ Mem., vol. 11, Tokyo: Math. Soc. Japan, pp. 95–145, MR 1862150
Zelevinsky, A. V. (1981), "A generalization of the Littlewood-Richardson rule and the Robinson-Schensted-Knuth correspondence", Journal of Algebra, 69 (1): 82–94, doi:10.1016/0021-8693(81)90128-9, ISSN 0021-8693, MR 0613858

외부 링크

리틀우드-리처드슨 규칙을 사용하여 슈르 기능의 제품을 분해하는 온라인 프로그램

[gao20-1] Gao, Shiliang; Orelowitz, Gidon; Yong, Alexander (2021). "Newell-Littlewood numbers". Trans. Amer. Math. Soc. 374 (9): 6331–6366. arXiv:2005.09012v1. doi:10.1090/tran/8375. S2CID 218684561.

[1]

Search