생명표

2003년 미국 사망률 표, 표 1 페이지

보험수리적 과학과 인구통계학에서 생명표(사망률표 또는 보험수리적표라고도 함)는 각 연령에 대해 그 연령의 사람이 다음 생일 전에 사망할 확률("사망 확률")을 나타내는 표다. 즉, 특정 인구로부터 생존하는 것을 나타낸다.^[1] 그것들은 또한 인구의 장수를 측정하는 장기 수학적인 방법으로 설명될 수 있다.^[2] 그라우트, 리드, 머렐, 키피츠, 그레빌 등 인구통계학자들이 표를 만들었다.^[2]

보험수리적 과학에 사용되는 생명표에는 두 가지 유형이 있다. 기간 수명표는 특정 모집단의 특정 기간 동안의 사망률을 나타낸다. 세대 수명표라고 불리는 코호트 수명표는 특정 모집단의 전체 수명 동안 전체 사망률을 나타내기 위해 사용된다. 그들은 같은 특정한 시간 간격 동안 태어나야 했을 것이다. 코호트 수명표는 미래에 예상되는 모집단의 사망률 변화를 예측할 수 있기 때문에 더 자주 사용된다. 이 유형의 표는 또한 시간이 지남에 따라 관찰될 수 있는 사망률의 패턴을 분석한다.^[3] 이 두 가지 유형의 생명표 모두 현재로부터 실제 인구를 바탕으로 만들어졌으며, 가까운 미래에 인구를 경험할 수 있는 교육적인 예측도 포함하고 있다.^[3] 실제 기대수명을 찾기 위해서는 100년이 지나야 하고, 그 때쯤이면 의료서비스가 지속적으로 발전하고 있기 때문에 데이터는 아무 소용이 없다는 것을 알게 될 것이다.^[4]

역사적 인구 통계에 있는 다른 생명표들은 비록 유아와 유아 사망률을 과소계상하는 경우가 많지만, 더 나은 기록을 가진 다른 지역과 비교하여, 그리고 출생 시 다양한 사망률 수준과 기대수명에 대한 수학적 조정을 바탕으로 할 수 있다.^[5]

이 시작점에서, 많은 추론을 도출할 수 있다.

특정 연령에서 생존할 확률
다른 연령대의 사람들의 남은 기대 수명은

생명표는 생물학과 역학에서도 광범위하게 사용된다. 이 도구를 사용하는 영역은 사회 보장이다. 그것은 사회보장제도를 가진 모든 사람들의 사망률을 조사하여 어떤 조치를 취해야 할지를 결정한다.^[3]

제품 수명주기 관리에서도 중요한 개념이다.

모든 사망률표는 환경 및 생명 환경에 특수하며, 그러한 환경 조건 내에서 예상되는 최대 나이를 확률적으로 결정하는 데 사용된다.

배경

생명표에는 두 가지 유형이 있다.

기간 또는 정적인 생명표에는 현재 사망 확률이 표시된다(연령이 다른 사람의 경우, 현재 연도)
코호트 수명표는 평생 동안 특정 코호트(특히 출생년)에서 사람이 사망할 확률을 보여준다.

정적인 생명표들은 세대와 겹치는 고정된 인구를 가정하는 개인을 표본으로 삼는다. 인구가 평형 상태에 있고 환경이 변하지 않는다면 "정적 생명표"와 "코호트 생명표"는 동일할 것이다. 만약 한 인구에게 매년 일정한 수의 사람이 생긴다면, 그것은 생명표로부터의 사망 확률은 완전히 정확하다는 것을 의미할 것이다. 또한, 매년 10만 명의 정확한 사람들이 이민이나 이민을 하지 않고 태어났다. ^[3] "생명표"는 코호트 생명표는 현재 시점까지의 데이터와 미래 사망률에 대한 먼 추정치를 사용하여만 구성할 수 있기 때문에 주로 기간 생명표를 가리킨다.

생명표는 미래 사망률 예측을 사용하여 구성할 수 있지만, 더 자주 그것들은 최근 연령별 사망률을 요약한 것이며, 반드시 추정치라고는 할 수 없다. 이러한 이유로, 생명표에서 대표되는 노년층은 이 코호트의 초기에는 존재하지 않았던 의학, 공중 보건 및 안전 표준의 현재 진보를 전제로 하기 때문에 이 연령대의 삶이 미래에 경험할 수 있는 것을 대표하지 못할 가능성이 더 클 수 있다. 생명표는 이상적으로는 폐쇄적인 인구통계학적 시스템 하에서 특정 인구의 사망률과 인구조사 수치에 의해 생성된다. 이것은 코호트를 분석할 때 이민과 이민이 존재하지 않는다는 것을 의미한다. 폐쇄형 인구통계시스템은 이주흐름이 무작위적이고 유의하지 않으며, 다른 인구에서 온 이민자들은 새로운 인구에서 온 개인과 동일한 사망위험을 가지고 있다고 가정한다. 사망률 표의 또 다른 이점은 인구 통계학이나 다른 모집단에 대한 예측에 사용할 수 있다는 것이다.^[6]

그러나 생활표에 표시되는 정보의 약점도 있다. 하나는 그들이 인구의 전반적인 건강 상태를 언급하지 않는다는 것이다. 세상에는 둘 이상의 질병이 존재하며, 한 사람이 동시에 다른 단계에서 둘 이상의 질병을 가질 수 있어 혼수상태라는 용어를 도입했다.^[7] 따라서 생명표 역시 사망률과 질병성의 직접적인 상관관계를 보여주지 않는다.^[8]

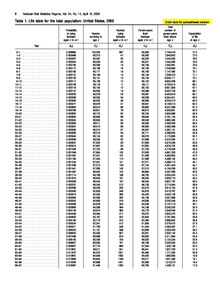
생명표에는 10만 명의 출생아로 구성된 단일세대가 살 수 있는 모든 연령대에서 사망률 체험을 관찰한다.^[3]

생명표는 사망률이 상당히 다르기 때문에 보통 남성과 여성을 위해 별도로 제작된다. 다른 특징들은 흡연 여부, 직업, 사회경제적 계층과 같은 다른 위험들을 구별하는데 사용될 수 있다.

수명표는 예를 들어 건강 기대치를 계산하기 위한 건강 정보와 같이 사망률 외에 다른 정보를 포함하도록 확장할 수 있다. 장애 조정 수명과 건강 수명과 같은 건강 기대 기간은 장애 없는 것과 같은 특정한 건강 상태에서 살기를 기대할 수 있는 남은 기간이다. 기대수명을 다양한 주에서 소비되는 수명으로 나누는 데에는 두 가지 유형의 수명표가 사용된다.

다중 상태 수명표(증분 감소 수명표라고도 함)는 다른 주 내외 및 사망에 대한 전환율을 기반으로 한다.
유병 기반 생명표(Sullivan 방법이라고도 함)는 각 주의 비율에 대한 외부 정보에 기초한다. 수명표는 또한 다른 노동력 상태 또는 혼인 상태에서의 기대수명을 나타내기 위해 연장될 수 있다.

모성 사망과 유아 도덕성과 관련된 생명표는 그들이 특정 인구와 함께 일하는 가족 계획 프로그램을 형성하는데 도움을 주기 때문에 중요하다. 그들은 또한 한 나라의 평균 수명을 다른 나라와 비교하는데 도움을 준다.^[9] 세계적으로 기대수명을 비교하는 것은 각국이 왜 한 나라의 기대수명이 크게 증가하는지 이해하는데 도움이 된다. 서로의 건강관리를 보고 아이디어를 그들 자신의 시스템에 채택함으로써 말이다.^[10]

보험적용

보험 상품의 가격을 책정하고, 적절한 적립금을 통해 보험 회사의 지불 능력을 보장하기 위해서, 보험 계약자는 미래의 보험 사건(사망, 질병, 장애 등)에 대한 예측을 개발해야 한다. 이를 위해, 작동자들은 사건의 속도와 타이밍에 대한 수학 모델을 개발한다. 그들은 최근 과거의 이러한 사건들의 발생률을 연구하고, 때로는 이러한 과거 사건들이 시간이 지남에 따라 어떻게 변화할 것인가에 대한 기대치(예를 들어 과거 사망률의 점진적인 감소가 계속될 것인가)를 발전시키고, 대개 나이나 다른 재생을 바탕으로 미래에 그러한 사건들의 예상 비율을 도출해냄으로써 이것을 한다.인구의 부수적 특성 액츄리어의 일은 사망 위험에 처한 사람들과 실제로 죽은 사람들 사이의 비교를 형성하여 각 나이 수에서 한 사람의 사망 확률을 계산하는 것인데, 방정식에서 qx로 정의된다.^[6] 모집단을 분석할 때 필요한 정보를 수집하는 데 사용되는 주요 출처 중 하나가 특정 모집단에 속하는 개별 기록을 취득하여 보험에 가입하는 것이다.^[6] 이러한 것들은 사망률을 나타내면 사망률표라고 하고, 다양한 종류의 질병이나 장애율을 보이면 병리표라고 한다.

컴퓨터의 이용 가능성과 개인에 대한 데이터 수집의 확산은 과거에 사용되었던 것보다 더 볼륨 있고 집중적인 계산을 가능하게 했다(즉, 그들은 더 많은 숫자를 깨부수며), 그리고 다른 용도에 대해 다른 표를 제공하려고 시도하고, 비전통적인 행동의 범위를 고려하는 것이 더 일반적이다.위험 평가를 위해 일부 기관이 사용하는 전문 계산에 rs(예: 도박, 부채 부하)를 포함시킨다. 특히 손해보험의 경우(예: 자동차보험의 가격결정은 많은 위험요소를 허용할 수 있으며, 이에 상응하여 복잡한 예상청구율표가 필요하다)가 이에 해당한다. 그러나 생명표라는 표현은 일반적으로 인간의 생존율을 가리키며 손해보험과는 관련이 없다.

수학

_t표_x 1의 p 관리도. 총 모집단에 대한 수명 표: 미국, 2003, 페이지 8

생명표에서 사용되는 기본 대수학은 다음과 같다.

$\,q_{x}$ $\,q_{x}$ ${\$ : 정확히 $\,x$ ${\displaystyle \,$ $\,(x+1)$ $}$ 의 나이가 되기 전에 사망할 $\,x$ 확률 $\,(x+1)$ + 1 $\,(x+1)$ ) ${\displaysty \,(x+1$
$\,p_{x}$ $\,p_{x}$ ${\$ : $\,x$ x $\,x$ 의 나이가 생존할 확률 $\,x$ $\,(x+1)$ + 1 $\,(x+1)$ ) ${\displaysty \,(x+1$

\,p_{x}=1-q_{x}}

$\,\ell _{x}$ $\,\ell _{x}$ ${\$ : $\,x$ 까지 생존하는 사람 수 ${\displaystyle$ \, $x}$

이는 일반적으로 10만명으로 측정되는

\,\ell _{0}

\,\ell _{0}

{\

의

\,\ell _{0}

수명을 라딕스^[11] 또는 시작점에 기초한다는 점에 유의하십시오.

\,\ell _{x+1}=\ell _{x}\cdot(1-q_{x}}=\ell _{x}\cdot p_{x}}}}

\,{\ell _{x+1} \over \ell _{x}=p_{x}}

$\,d_{x}$ x ${\$ : 지난 $\,x$ 생일 때 $\,x$ $\,x$ 이(가) 사망한 사람 수

{\d_{x}=\ell _{x}-\ell _{x}-\ell _{x+1}=\ell _{x}\cdot(1-p_{x})=\ell _{x}\cdot q_{x}}}}}}

$\,{}_{t}p_{x}$ $\,{}_{t}p_{x}$ $\,{}_{t}p_{x}$ ${\$ : 정확히 $\,x$ $\,x$ 이(가) $\,t$ $\,t$ 년 $\,x+t$ 이상 $\,t$ 생존할 $\,x$ 확률( $\,x+t$ : x + ${\displaystystyle \,x+t}).$

\,{}_{t}p_{x}={\ell _{x+t} \over \ell _{x}}

$\,{}_{t\mid k}q_{x}$ $\,{}_{t\mid k}q_{x}$ $\,{}_{t\mid k}q_{x}$ x ${\$ : 정확하게 $\,x$ $\,t$ 동안 $\,t$ 생존한 후 다음 $\,k$ $\,k$ 년 $\,k$ 내에 사망할 확률 $\,x$

\,{}_{t\mid k}q_{x}={}_{t}p_{x}\cdot {}_{k}q_{x+t}={\ell _{x+t}-\ell_{x+t+k}\c}\over \ell_{x}}}}}

μ_x : 사망률의 힘, 즉 x세의 순간사망률, 즉 x세부터 시작되는 짧은 간격으로 사망하는 사람의 수를 μ로_x 나누고 또한 그 간격의 길이로 나눈다.

또 다른 공통 변수는

$\,m_{x}$

이 기호는 중앙 사망률을 가리킨다. 그것은 대략 평균 사망률과 동일하며, 연령에 걸쳐.

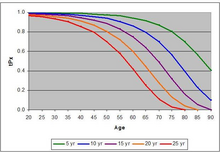
추가 설명: 변수 dx는 연속된 두 연령 수 내에서 발생할 사망자 수를 의미한다. 그 예로는 7세에서 8세 사이에 기록된 코호트의 사망자 수가 있다. dx와 정반대라는 뜻의 변수 ℓx는 연속된 두 살 사이에 살았던 사람들의 수를 나타낸다. 0의 ℓ은 10만과 같다. 변수 Tx는 세대 내 모든 구성원이 각각의 나이 x를 초과하여 산 해를 의미한다. ėx는 이미 특정 연령의 회원들의 기대수명을 나타낸다.^[3]

사망률 표 끝내기

실제로 사망률표와 관련된 궁극적인 나이를 갖는 것이 유용하다. 일단 최종 연령에 도달하면 사망률은 1.000으로 가정한다. 이 나이가 생존자에게 생명보험급여가 지급되거나 연금지급이 중단되는 시점이 될 수 있다.

사망률 표를 끝내기 위해 네 가지 방법을 사용할 수 있다.^[12]

강제 방법: 최종 연령을 선택하고 그 연령의 사망률을 다른 사망률의 변화 없이 1.000으로 설정하십시오. 이것은 궁극의 나이에 음경 및 이전 나이와 비교했을 때 불연속성을 만들어낸다.
혼합 방법: 궁극의 나이를 선택하고, 몇 명의 더 이른 나이부터의 비율을 혼합하여 최종 나이에 1.000명으로 부드럽게 융화될 수 있도록 하라.
패턴 방법: 사망률의 패턴이 1,000에 도달할 때까지 계속되도록 하고 그것을 궁극의 나이로 설정한다.
한 개 미만의 방법: 이것은 강제적인 방법에 대한 변형이다. 최종 사망률은 강제적 방법에서와 같이 1.000이라기보다는 선택된 최종 연령에서 예상되는 사망률과 동등하게 설정된다. 이 비율은 1.000 미만이 될 것이다.

역학

역학 및 공중 보건에서 설리번과 다중 상태 수명표(건강 기대치를 계산하는 데 사용됨)는 물론 표준 수명표(수명을 계산하는 데 사용됨)는 모두 가장 일반적으로 수학적으로 사용되는 장치다. 후자는 사망률 외에도 건강에 대한 정보를 포함한다. 역학학자들은 연구 대상 연도의 기대 수명을 관찰함으로써 질병이 전반적인 사망률 상승에 기여하고 있는지 여부를 확인할 수 있다.^[13] 역학학자들은 인구통계학자들이 기대수명의 급격한 감소를 특정 인구에서 발생하고 있는 건강문제와 연관시킴으로써 이해하는데 도움을 줄 수 있다.^[13]

참고 항목

메모들

^ Harper, Begon. "Cohort Life Tables". Tiem. Retrieved 9 February 2015.
^ Jump up to: ^a ^b "Life Table: Meaning, Types and Importance". Sociology Discussion - Discuss Anything About Sociology. 2016-07-21. Retrieved 2018-03-30.
^ Jump up to: ^a ^b ^c ^d ^e ^f Bell, Felicitie. "LIFE TABLES FOR THE UNITED STATES SOCIAL SECURITY AREA 1900–2100". Social Security. Retrieved 9 February 2015.
^ Silcocks, P. B. S.; Jenner, D. A.; Reza, R. (2001-01-01). "Life expectancy as a summary of mortality in a population: statistical considerations and suitability for use by health authorities". Journal of Epidemiology & Community Health. 55 (1): 38–43. doi:10.1136/jech.55.1.38. ISSN 0143-005X. PMC 1731769. PMID 11112949.
^ 사스키아 힌, 로마 이탈리아의 인구학, 캠브리지 대학 출판부, 2013 페이지 104–118.
^ Jump up to: ^a ^b ^c Pavía, Jose. "Introducing Migratory Flows in Life Table Construction" (PDF). Upcommons. Retrieved 10 February 2015.
^ Barendregt, Jan J (September 2009). "Coping with multiple morbidity in a life table". Mathematical Population Studies. 7 (1): 29–49. doi:10.1080/08898489809525445. PMID 12321476.
^ admin (2010-06-28). "Life-tables and their demographic applications". Health Knowledge. Retrieved 2018-03-30.
^ "Life Table: Meaning, Types and Importance". Sociology Discussion - Discuss Anything About Sociology. 2016-07-21. Retrieved 2018-03-30.
^ Roser, Max (2013-05-23). "Life Expectancy". Our World in Data. Retrieved 2018-04-12.
^ "Period Abridged Life Tables". avon.nhs.uk. Archived from the original on 2012-01-20.
^ "Ending the Mortality Table" (PDF). soa.org.
^ Jump up to: ^a ^b Bernstein, Lenny (2016-12-08). "U.S. life expectancy declines for the first time since 1993". Washington Post. ISSN 0190-8286. Retrieved 2018-03-29.

참조

Shepard, Jon; Robert W. Greene (2003). Sociology and You. Ohio: Glencoe McGraw–Hill. pp. A-22. ISBN 0-07-828576-3.
"Life Expectancies". Office of the State Actuary. 2008-09-22. Retrieved 2008-01-16.
Preston, Samuel H.; Patrick Heuveline; Michel Guillot (2001). Demography: measuring and modeling population processes. Blackwell Publishers. ISBN 1-55786-214-1.^{[페이지 필요]}

추가 읽기

Weisstein, Eric W. "Life expectancy". MathWorld.

외부 링크

[Cohort-1] Harper, Begon. "Cohort Life Tables". Tiem. Retrieved 9 February 2015.

[:0-2] Jump up to: ^a ^b "Life Table: Meaning, Types and Importance". Sociology Discussion - Discuss Anything About Sociology. 2016-07-21. Retrieved 2018-03-30.

[SS-3] Jump up to: ^a ^b ^c ^d ^e ^f Bell, Felicitie. "LIFE TABLES FOR THE UNITED STATES SOCIAL SECURITY AREA 1900–2100". Social Security. Retrieved 9 February 2015.

[4] Silcocks, P. B. S.; Jenner, D. A.; Reza, R. (2001-01-01). "Life expectancy as a summary of mortality in a population: statistical considerations and suitability for use by health authorities". Journal of Epidemiology & Community Health. 55 (1): 38–43. doi:10.1136/jech.55.1.38. ISSN 0143-005X. PMC 1731769. PMID 11112949.

[5] 사스키아 힌, 로마 이탈리아의 인구학, 캠브리지 대학 출판부, 2013 페이지 104–118.

[Upcommons-6] Jump up to: ^a ^b ^c Pavía, Jose. "Introducing Migratory Flows in Life Table Construction" (PDF). Upcommons. Retrieved 10 February 2015.

[7] Barendregt, Jan J (September 2009). "Coping with multiple morbidity in a life table". Mathematical Population Studies. 7 (1): 29–49. doi:10.1080/08898489809525445. PMID 12321476.

[8] (2010-06-28). "Life-tables and their demographic applications". Health Knowledge. Retrieved 2018-03-30.

[:02-9] "Life Table: Meaning, Types and Importance". Sociology Discussion - Discuss Anything About Sociology. 2016-07-21. Retrieved 2018-03-30.

[10] Roser, Max (2013-05-23). "Life Expectancy". Our World in Data. Retrieved 2018-04-12.

[11] "Period Abridged Life Tables". avon.nhs.uk. Archived from the original on 2012-01-20.

[12] "Ending the Mortality Table" (PDF). soa.org.

[:1-13] Jump up to: ^a ^b Bernstein, Lenny (2016-12-08). "U.S. life expectancy declines for the first time since 1993". Washington Post. ISSN 0190-8286. Retrieved 2018-03-29.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

hide 권한통제
일반	통합 권한 파일(독일)
국립도서관	미국 일본.
기타	마이크로소프트 어학

Search

생명표

네임스페이스

더

목차

배경

보험적용

수학

사망률 표 끝내기

역학

참고 항목

메모들

참조

추가 읽기

외부 링크