항목 트리 분석
Item tree analysis항목 트리 분석(ITA)은 설문지의 항목에 계층 구조를 구성하거나 관측된 응답 패턴에서 테스트를 수행할 수 있는 데이터 분석 방법이다.
우리가 m항목을 가진 설문지를 가지고 있고, 피험자가 이러한 항목 각각에 대해 긍정(1) 또는 부정(0)으로 답할 수 있다고 가정하자. 즉, 그 항목은 이분법적이다.n개의 피험자가 항목에 응답하면 m 열과 n개의 행으로 이루어진 2진수 데이터 행렬D가 된다.이 데이터 형식의 대표적인 예는 과목별로 풀 수 있는 (1) 또는 실패(0) 항목이다.다른 대표적인 예로는 항목이 피험자가 동의할 수 있거나 동의하지 않을 수 있는 진술인 질문지를 들 수 있다.
항목의 내용에 따라 항목 j의 대상자의 반응이 다른 항목에 대한 대상자의 반응을 결정할 수 있다.예를 들어 항목 j에 동의하는 각 주체도 항목 i에 동의할 가능성이 있다.이 경우, 해당 항목은 i(짧은 → j 항목이라고 한다.ITA의 목표는 데이터 세트D로부터 그러한 결정론적 영향을 파악하는 것이다.
ITA 알고리즘
ITA는 원래 1974년 반 리우에 의해 개발되었다.[1]다음에 우리가 고전적인 ITA라고 부르는 그의 알고리즘의 결과는 논리적으로 일관된 함의 → j → j 이다 논리적으로 일치한다는 것은 만약 내가 j와 j를 내포한다면 항목들의 각 3중 i, j, k에 대해 k를 내포한다는 것을 의미한다.따라서 ITA의 결과는 항목 집합에 대한 반사적 및 전이적 관계, 즉 항목에 대한 준순서가 된다.
ITA를 수행하기 위한 다른 알고리즘이 Schrepp(1999년)에서 제안되었다.이 알고리즘을 귀납적 ITA라고 한다.
고전적 ITA와 귀납적 ITA는 모두 탐색적 데이터 분석에 의해 설정된 항목에 준순서를 구성한다.그러나 두 방법 모두 이 준순서를 구성하기 위해 다른 알고리즘을 사용한다.주어진 데이터 세트의 경우 통상 고전적 ITA와 귀납적 ITA의 결과 준순서는 다를 것이다.
고전적 및 귀납적 ITA에 사용되는 알고리즘에 대한 자세한 설명은 Schrepp(2003) 또는 Schrepp(2006)[1]에서 확인할 수 있다.최근 논문(Sargin & Unlü, 2009)에서는 유도 ITA 알고리즘에 대한 일부 수정이 제안되며, 이 수법은 데이터로부터 정확한 함의를 검출하는 능력을 향상시킨다(특히 무작위 응답 오류율이 더 높은 경우).
다른 방법과의 관계
ITA는 설문지의 부울 분석이라는 데이터 분석 방법 그룹에 속한다.부울 분석은 1976년 플라멘트에 의해 도입되었다.[2]부울 분석의 목적은 질문지 또는 테스트의 항목 사이에 결정론적 의존성(예를 들어 항목을 하는 부울 논리로부터 나온 공식 →j → → → j → j → → k → j∨ → → k→ i을 검출하는 것이다.Flament(1976년)의 기초 작업 이후, 부울 분석을 위한 여러 가지 다른 방법이 개발되었다.예를 들어 Van Buggenaut과 Degenf(1987), Duquenne(1987), Theuns(1994)를 참조하십시오.이러한 방법들은 데이터로부터 설문지 항목들 사이의 결정론적 의존성을 도출하는 목표를 공유하지만, 이 목표에 도달하기 위한 알고리즘은 다르다.ITA와 부울 데이터 분석의 다른 방법의 비교는 Schrepp(2003)에서 찾을 수 있다.
적용들
항목 트리 분석의 구체적인 적용에 대해 설명하는 몇 가지 연구 논문이 있다.Hold and Korossy(1998)는 고전적인 ITA와 함께 일련의 대수 문제에 대한 함의를 분석한다.항목 트리 분석은 또한 이분법적 데이터의 구조에 대한 통찰력을 얻기 위해 여러 사회과학 연구에도 사용된다.예를 들어 Bart와 Krus(1973년)에서는 ITA의 전신으로 사회적으로 받아들여지지 않는 행동을 기술하는 항목에 대해 계층적 질서를 확립하는 데 사용된다.얀센스(1999)에서는 부울 분석의 방법을 사용하여 지배적인 문화의 가치 체계로 소수민족의 통합 과정을 조사한다.Schrepp는[3] 사회과학 질문지 항목들 사이의 의존성 분석에서 몇 가지 유도 ITA의 적용을 설명한다.
응용 프로그램의 예
ITA가 설정한 데이터의 분석 가능성을 보여주기 위해 우리는 귀납적 및 고전적 ITA에 의해 1995년 국제사회과학조사프로그램(ISSSP)의 질문 4의 문장을 분석한다.ISSSP는 사회과학 연구의 중요한 주제를 다루는 조사에 관한 국가간 협력의 연례 프로그램이다.이 프로그램은 매년 참가국별로 비교 가능한 질문으로 설문조사를 실시한다.1995년 조사의 주제는 국민 정체성이었다.우리는 서독의 데이터 세트에 대한 질문 4에 대한 결과를 분석한다.질문 4에 대한 진술은 다음과 같다.
어떤 사람들은 다음과 같은 것들이 진정한 독일인이 되기 위해 중요하다고 말한다. 다른 이들은 그들이 중요하지 않다고 말한다. 다음 각 항목이 얼마나 중요하다고 생각하십니까?
1. 독일에서 태어났으면
2. 독일 시민권을 가지다
3. 인생의 대부분을 독일에서 살았다는 것
4. 독일어를 할 수 있다
5. 기독교인이 되다
6. 독일의 정치 제도를 존중하다
7. 독일어를 느끼다
피실험자들은 응답 가능성을 매우 중요하고, 중요하고, 매우 중요하지 않고, 전혀 중요하지 않으며, 그리고 진술에 대답하는 것을 선택할 수 없었다.이 데이터 세트에 ITA를 적용하기 위해 답변 범주를 변경했다.
매우 중요하고 중요한 것은 1로 코딩된다.별로 중요하지 않고 전혀 중요하지 않은 것은 0으로 코딩되어 있다.선택할 수 없음은 결측 데이터로 처리되었다.
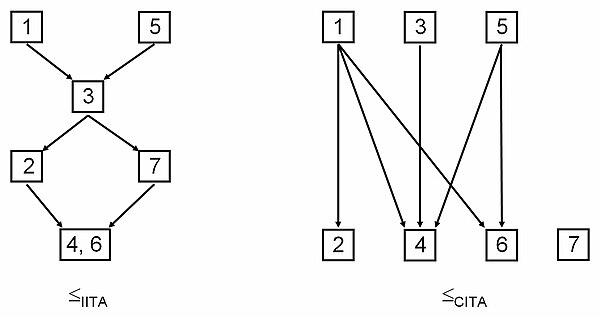
다음 그림은 결과적인 준주문 A ITA 및from C T 의 클래식 ITA의
사용 가능한 소프트웨어
ITA 2.0 프로그램은 고전적 ITA와 귀납적 ITA를 모두 구현한다.그 프로그램은 [2]에서 이용할 수 있다.프로그램에 대한 간단한 문서는 [3]에 수록되어 있다.
참고 항목
메모들
참조
- 바트, W. M. & Krus, D. J. (1973)항목 간의 계층 구조를 결정하는 순서 이론적 방법.교육 및 심리 측정, 33, 291–300.
- 뒤켄 5세(1987년).유한 격자에 대한 속성과 일부 표현 특성 사이의 개념적 의미B Ganter, R Wille, K Wolfe(에드)에서 Beitrége jur Begriffsanalyse:Vortrége der Arbitstagung Begriffsanalyse, Darmstadt 1986, 페이지 313–339.Wissenschafts-Verlag, Mannheim.
- 플랜트 C(1976년).L'Analyse Bool'eenne de Question.무튼, 파리.
- Hold, T, & Korossy, K. (1998년)이론적으로 근거한 항목 구조를 확립하기 위한 경험적 경험으로서의 데이터 분석.제이츠히프트 퓌르 사이코로니, 206, 169–188.
- 얀센스, R. (1999년)그룹 프로세스 및 태도 측정에 대한 부울 접근법.예로서 통합의 개념.수학 사회과학, 38, 275–293.
- 슈렙 M(1999년).이중평가 시험항목의 시사점 구축에 관한 연구수학 사회과학, 38(3), 361–375.
- 슈렙, M(2002년).설문지의 부울 분석을 통한 경험적 데이터의 탐색적 분석.제이츠히프트 퓌르 심령술사, 210/2, S. 99-109
- 슈렙, M. (2003)설문지 항목 간의 계층적 종속성을 분석하는 방법.심리학적 연구의 방법, 19, 43–79.
- 슈렙, M. (2006년)ITA 2.0: 고전적 및 귀납적 항목 트리 분석을 위한 프로그램.통계 소프트웨어 저널, 제16권, 제10호
- 슈렙, M. (2006년)상관 일치 계수의 속성:뮐뤼&알베르트(2004)에게 한 마디.수학 사회과학, 제51권, 제1호, 제117–123호.
- 슈렙, M. (2007)준주문 적합성 대책 평가에 관하여.수학 사회과학 제53권 제2호, 196–208.
- Theuns P (1994년).수량화 가능한 Coucurence 데이터의 부울분석을 위한 이분법G Fischer, D Laming(에드), 수학 심리학, 심리측정학 및 방법론, 과학 심리학 시리즈, 페이지 173–194.스프링거-베를랙, 뉴욕.
- 울른위, A, & 알버트, D. (2004)상관 계수 CA - 기술 적합도 측도의 수학적 분석.수학 사회과학, 48, 281–314.
- Van Buggenhaut J, Degf E (1987년).설문지의 부울분석에 있어서의 이분법적 방법에 관한 연구E Roskam, R Suck (eds)에서 수학 심리학 진행 중, 엘시어 과학 출판사 B.V., 북 홀랜드.
- J.F.J. (1974년) 반 리우웨.항목 트리 분석네델란드 티즈쉬리프트 보어 드 사이코로지, 29, 475–484.
- 사긴, A, & 우른뤼, A. (2009)유도 품목 트리 분석:수정, 개선 및 비교.수학 사회과학, 58, 376–392.