헌의 방법

수학 및 계산 과학에서 헌의 방법은 개선되거나^[1] 수정된 오일러의 방법(즉, 명시적 사다리꼴 규칙^[2])이나 이와 유사한 2단 런지-쿠타 방법을 가리킬 수 있다.칼 쉰의 이름을 따서 지었으며, 주어진 초기값으로 보통의 미분방정식(ODE)을 푸는 숫자적 절차다.두 변형 모두 오일러 방식을 2단계 2차 룬게-쿠타 방식으로 확장한 것으로 볼 수 있다.

초기값 문제에 대한 숫자 솔루션을 계산하는 절차:

${\displaystyle y'(t)=f(t,y(t),\qquad \qquad y(t_{0})=y_{0},}$

헌의 방법으로 우선 중간값 $y{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle {\mathrm{i}}_{}}$+ ${\displaystyle 1_{}}$ ${\$을 계산한$$ 후 다음 통합 지점에서 최종$$ 근사 y ${\displaystyle i_{}}$+ ${\displaystyle 1_{}}$ ${\$를 계산한다.

${\displaystyle {\tilde{y}_{i+1}=y_{i}+hf(t_{i},y_{i}}}}}}$

${\displaystyle y_{i+1}=y_{i}+{\frac {h}{{h}}{2}}[f(t_{i},y_{i}}}]+f(t_{i+1},{\tilde {y}}_{i+1}],}$

여기서 $h{\displaystyle }$ ${\displaystyle h}$은(는) 단계 크기이고 $t{\displaystyle {}_{}}$ ${\displaystyle i_{}}$+ ${\displaystyle 1_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$+ ${\displaystyle h}$ ${\displaystyle t_{i+1}=t_{i}+h}$.

설명

오일러의 방법은 허언의 방법의 근간으로 쓰인다.오일러의 방법은 스텝 크기가 작을 경우 오차가 작을 것으로 가정하여 간격의 시작 부분에 있는 함수의 기울기를 추정하여 함수에 접하는 선을 추정하는 것으로 사용한다.그러나 극히 작은 스텝 크기를 사용하더라도 많은 스텝에 걸쳐 오차가 누적되기 시작하고 추정치는 실제 기능 값과 다르다.

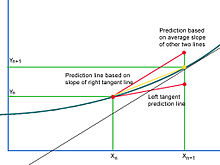
용액 곡선이 위로 오목한 경우, 접선선은 다음 점의 수직 좌표를 과소평가하며, 그 반대도 오목한 아래 용액에 대해 과소평가한다.이상적인 예측 선은 다음 예측 지점에서 곡선에 도달할 것이다.현실적으로 용액이 오목한 것인지, 오목한 것인지 알 길이 없고, 따라서 다음 예측점이 그 수직적 가치를 과대평가하거나 과소평가하게 될 것인지도 알 수 없다.곡선의 구체성은 어느 한쪽의 일관성을 보장할 수 없으며 예측은 해결책 영역의 서로 다른 지점에서 과대평가 및 과소평가될 수 있다.Hun's Method는 탄젠트 라인 세그먼트에 걸쳐 있는 간격을 전체적으로 고려하여 이 문제를 해결한다.오목한 예를 들어 왼쪽 접선 예측선은 현재 점부터 다음 예측점까지의 구간의 전체 폭에 대해 곡선의 기울기를 과소평가한다.오른쪽 끝점에 있는 접선을 고려한다면( 오일러의 방법을 사용하여 추정할 수 있다), 정반대의 문제가 있다. 왼쪽 끝점의 접선선을 따라 있는 점들은 수직 좌표를 가지며, 모두 고려 중인 구간의 오른쪽 끝점을 포함하여 해결 곡선에 놓여 있는 점들을 과소평가한다.해결책은 경사를 어느 정도 크게 하는 것이다.Hun's Method는 구간의 양쪽 끝에서 용액 곡선에 대한 접선 선을 고려하는데, 하나는 과대평가하고 하나는 이상적인 수직 좌표를 과소평가한다.예측 선은 오일러의 방법을 사용하여 대략적인 우측 끝점 접선의 경사만을 기준으로 작성해야 한다.이 경사가 구간의 왼쪽 끝점을 통과하면 결과는 이상적인 예측선으로 사용하기에는 명백하게 너무 가파르고 이상적인 점을 과대평가한다.따라서 이상적인 지점은 두 경사면의 평균인 잘못된 과대평가와 과소평가 사이의 대략 중간 정도에 있다.

오일러의 방법은 용액에서 다음 점의 좌표를 대략 추정하는 데 사용되며, 이 지식을 이용하여 원래의 추정치를 다시 예측하거나 수정한다.^[4]방정식의 오른쪽에 있는$$ 수량 $f{\displaystyle (}$ ${\displaystyle x}$, ${\displaystyle y}$) ${\$$displaystyle \textstyle$ $f($$x,y)}$을 임의의 지점$({\displaystyle x}$, y${\displaystyle }$)에서 추구하는 해결책의 기울기로 생각할 수 있다고 가정하면$,$ 이는 다음 지점의 오일러 추정치와 결합하여 th에서 접선 선의 기울기를 제공할 수 있다.e 오른쪽 끝점다음으로 두 기울기의 평균은 오른쪽 끝 구간의 보정된 좌표를 찾는 데 사용된다.

파생

${\displaystyle {\text{Slope}_{\text{left}}=f(x_{i},y_{i}})}$

${\displaystyle {\text{Slope}_{\text}}=f(x_{i}+h,y_{i}+h,y_{i}+hf(x_{i},y_})}}$

${\displaystyle {\text{Slope}_{\text{ideal}}={\frac {1}{1}:{1}2}}({\text{Slope}}}}}{\text{Slope}}}}{\text}{\text}}}}}}}}}}}}}$

선의 기울기가 상승/달림과 동일하다는 원리를 사용해 구간 끝의 좌표를 다음 공식을 이용해 찾을 수 있다.

${\displaystyle {\text{Slope}_{\text{ideal}}={\frac {\Delta y}{h}}}}$

${\displaystyle \Delta y=h({\text{Slope}_{\text{ideal}})}$

${\displaystyle x_{}}$ ${\displaystyle i_{}}$+ ${\displaystyle 1_{}}$= x ${\displaystyle i{}_{}}$+ h ${\displaystyle x_{i+1}=x_{i}+h$ $y{\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$= y +${\displaystyle {}_{}\mathrm{\Delta y}}$ ${\$ y$}$

${\displaystyle y_{i+1}=y_{i}+h{\text{Slope}_{\text{ideal}}}}}$

${\displaystyle y_{i+1}=y_{i}+{\frac {1}{1}{1}{{\text{Slope}}}{\text{{Left}}+{\text}}{Slope}_{\text}}}}}}}}$

${\displaystyle y_{i+1}=y_{i}+{h}{\frac {h}{{h}}(f(x_{i}},y_{i})+f(x_{i}+h,y_}+hf(x_{i}},y_{i})}}}}}}}}}$

오일러 방법의 정확도는 스텝 크기가 줄어들면서 선형적으로만 향상되는 반면 헌 방법은 2차적으로 정확도를 향상시킨다.^[5]The scheme can be compared with the implicit trapezoidal method, but with ${\displaystyle f(t_{i+1},y_{i+1})}$ replaced by ${\displaystyle f(t_{i+1},{\tilde {y}}_{i+1})}$ in order to make it explicit.${\displaystyle {\stackrel{}{y}}_{}}$~ ${\displaystyle i_{}}$+ ${\displaystyle 1_{}}$ ${\${i+$1}$은(는) 동일한 초기값 문제에 대한 오일러의 방법의 한 단계의 결과물이다$$.그래서 헌의 방법은 전방 오일러의 방법을 예측자로 하고 사다리꼴 방법을 교정자로 하는 예측 변수-코렉터 방법이다.

룬게-쿠타법

개량된 오일러의 방법은 2단 룬게-쿠타 방식으로, 푸에르토 테이블라우(존 C 이후)를 사용하여 쓸 수 있다. 도살자:

	0
	1	1
		1/2	1/2

헌의 방법(랄스턴의 방법이라고도 함)이라고 하는 다른 방법에는 다음과 같은 푸줏대감이 있다.^[6]

	0
	2/3	2/3
		1/4	3/4

이 방법은 잘림 오류를 최소화한다.

참조

위키미디어 커먼즈에는 허언의 방법과 관련된 미디어가 있다.