해밀턴 제약

해밀턴 제약조건은 해밀턴 공식을 인정하고 재측정 불변인 이론에서 발생한다.일반 상대성 이론의 해밀턴 제약은 중요하지 않은 중요한 예이다.

일반 상대성 이론의 맥락에서, 해밀턴 제약은 기술적으로 공간 좌표와 시간 좌표 모두에서 이론의 재측정성을 반영하는 공간 및 시간 미분 동형 제약의 선형 조합을 참조한다.그러나 대부분의 시간 동안 해밀턴 제약이라는 용어는 시간 미분 동형을 생성하는 제약 조건을 위해 예약되어 있습니다.

가장 간단한 예: 파라미터화된 시계와 진자 시스템

파라미터화

통상적인 설명에서 고전 역학은 독립된 변수로써 특별한 역할을 하는 것으로 보인다.그러나 이것은 불필요하다.역학은 시간변수를 비록 지정되지 않았지만 공통의 파라미터 변수의 관점에서 파라미터화함으로써 확장된 위상공간의 다른 변수와 동일한 기초에서 시간변수를 취급하도록 공식화할 수 있다.위상 공간 변수가 동일한 기반에 있습니다.

\tau

는

클럭의

판독

시간 t와 진자의

신장

x(\

displaystyle

x) 사이의

t

x

다른 가능한 상관관계를 나타내는 비물리적 파라미터로

§

{

displaystyle \tau}

를

\tau

소개한다.

§

(\displaystyle

\displaystyle

\

displays)는

\tau

물리적인 파라미터가 아니기 때문에 다양한 선택지가

\tau

.

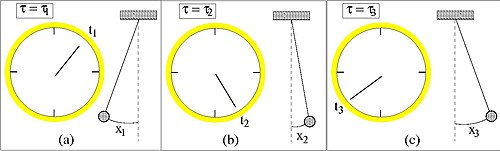
우리의 시스템이 단순한 고조파 운동을 실행하는 진자와 시계로 구성되어 있다고 가정해 보자.시스템은 x=x(t) 위치에 따라 고전적으로 기술할 수 있지만, x와 t의 관계가 직접 지정되지 않은 경우 x( {\ $\tau$ \ $displaystyle$ \ $displaystyle$ $\tau$ $\tau$ 및 $(\displaystyle$ \ $display$ $\tau$ 와 동일한 시스템을 기술할 수도 있습니다.대신 x와 t는 파라미터 $"\displaystyle\tau$ 에 의해 결정됩니다.이 파라미터는 단순히 시스템의 파라미터일 뿐 그 자체로는 객관적인 의미가 없을 수 있습니다.

시스템은 중심으로부터의 진자 위치( $\displaystyle$ x $x$ 와 시계상의 $판독치$ ( $t\displaystyle$ t $t$ 로 설명됩니다.이러한 $\tau$ 은 가상의 파라미터 $\tau$ {\\ $displaystyle$ 를 도입하여 동일한 기초에 놓았습니다.

$\displaystyle x(\displaystyle),\;\;\;t(\displaystyle)}$

$§(\display\display})$ 에 $\tau$ 대한 'display'는 시계에서의 변위와 판독치 사이의 가능한 모든 상관관계를 지속적으로 보여줍니다. $\tau '=f(\tau )$ $\tau$ {$\ $displaystyle$ \displaystyle $\tau$ )는 $\tau$ 단조함수 $=$ f $(\displaystyle$ \ $displaystyle$ '= $f(\displaystyle)'$ 로 대체할 수 있습니다 $\tau '=f(\tau )$ 이것이 시스템 재매개변성을 불변하게 하는 원인입니다.이 재매개 불변성에 의해 이론에서는 특정 $\tau$ 인 ${\(\displaystyle \tau)$ 에 $\tau$ 대해 x $))$ { $displaystyle$ x $(\$ $tau$ $)}$ $t(\tau )$ t $t(\tau )$ ${$$ { $displaystyle$ t(\tau $)}$ 의 $x (\tau)$ $t (\tau)$ 값을 예측할 수 없으며 이들 양 사이의 관계만 예측한다는 점에 유의하십시오.그런 다음 이 관계에 따라 역학이 결정됩니다.

이 리파라메트리제이션 불변계의 역학

그parametrized 조화 진동자의 작용이다.

$S=\int d\tau{\Big)}.$

어디){\displaystyle)}고{\displaystyle지}은 정준 좌표 및 p{p\displaystyle}과 동업-({\displaystyle p_{t}}그들의 켤레 momenta 있고 우리의 확장된 위상 공간(우리는 이 식의 평소 뉴턴의 방정식을 회수할 수 있을지 보여 줄 것이다)을 대표하지 않는다.로 액션을 쓰는 것

${\displaystyle S=\int d\tau{\Big)}}.$

우리는}}로 H{\displaystyle{{H\mathcal}를 확인한다.

${\displaystyle{{H\mathcal}}(x,t,\lambda, p,p_{t})=\lambda{\Big(}p_{t}와{p^{2}\over 2m}+1\over 2}m\omega{2}x^{2}{^\Big)}.}$

λ{\lambda\displaystyle}에 해밀턴의 방정식이 있다.

${\displaystyle{\partial{{H\mathcal}}\over\partial \lambda}=0}.$

어떤 제약 조건을 준다,

$C=p_{t}+{p^{2}\over 2m}+{1\over 2}m\omega ^{2}x^{2}=0.$

C{C\displaystyle}는 우리의 해밀턴 제약 조건!또한 오일러-라그랑주 운동 방정식에서도 얻을 수 있으며, 작용은 $\tau$ $\displaystyle\lambda$ 에 $\lambda$ 따라 달라지지만 $δ$ \displaystyle\ $tau }$ 도함수에 $\tau$ 따라 달라지지 않는다.다음으로 확장 위상공간 $변수$ x {\ $displaystyle$ x $x$ $t$ {\ $displaystyle$ t $t$ $p$ {\ $displaystyle$ p $p$ 및 $p_{t}$ ${\$ 는 $p_{t}$ 확장 위상공간의 이 제약조건 하이퍼서페이스 값을 취하도록 제한됩니다. $\lambda C$ 는 $§$ C { $displaystyle$ \ $lambda$ C}를 $\lambda C$ "smared" 해밀턴 제약조건이라고 부릅니다. $\lambda$ 서 $§$ { $displaystyle \lambda$ }는 $\lambda$ 임의의 숫자입니다.해밀턴 제약조건은 확장된 위상공간변수(또는 그 함수)가 $\tau$ \ $displaystyle$ 대해 어떻게 진화하는지 알려준다.

$({displaystyle {displaystyle \over d\displayda C\}={x,\;\;\;\;\;{dp \over d\display}\;\;\;{dp,\dp}\;\;\dp}\;{dp,\isplayda C\over C\c\c\;\c}\;\;\;\dp;\;\dp;\dp;\dp;\dp;\dp.$

(이것들은 실제로 다른 해밀턴의 방정식이다.)이 방정식은 위상 공간의 흐름 또는 궤도를 나타냅니다.일반적으로는

${dF(x,p,t,p_{t})\over d\clambda }=\{F(x,p,t,p_{t}),\lambda C\$

모든 위상 $공간$ 함수F {\ $displaystyle$ F $F$ 해밀턴 제약 조건 Poisson이 자체와 교신할 때 자신을 보존하고 따라서 제약 조건-초서면을 보존합니다. $x(\tau )$ ( $x(\tau )$ ) { $displaystyle$ x ( \ $tau$ ) $t(\tau )$ } $t(\tau )$ ( t ( \ $displaystyle t$ ( \ tau $t(\tau )$ )}와 $x (\tau)$ $t (\tau)$ $t(\tau )$ 측정 가능한 양 사이의 상관관계는 구속 표면 내의 제약조건에 의해 생성된 'orbits'에 대응하며, $p(\tau )$ 의 특정 궤도는 예를 들어 p $p(\tau )$ ( $)$ )의 값을 측정한다고 한다. $style$ p $x(\tau )$ $displaystyle$ x $(\displaystyle$ $)}$ 와 $p (\tau)$ $x (\tau)$ $x(\tau )$ $t(\tau )$ displaystyle x $(\display))$ 및 t $t(\tau )$ $displaystyle$ t(\display $))$ 와 $t (\tau)$ $x(\tau )$ $(\displaystyle$ t $(\$ $display)$ 의 $\tau$ $t (\tau)$ $x (\tau)$ $t(\tau )$ 측정값에 $x(\tau )$ $t(\tau )$ 이 $가능합니다.$

패러메트리제이션 해제

해밀턴 역학의 다른 방정식은 다음과 같다.

$\displaystyle {displaystyle \over d\mathcal {H} \over \mathcal p} = - {\mathcal {H} \over \mathcal x} = \over \mathcal {H} \over d\mathcal } = - {\mathcal {\mathcal {H} \over x} } \mathcal {\mathcal } } } ; \ } } } } {\ {\ 、 \mathcal {\mathcal } }$

우리의 행동을 대체하면

$\displaystyle {displaystyle \over d\dp } =\dp {p \over m},\;\;\;\;{dp \over d\dp } =\displayda,\;\;\;\;\dp } =-\dp \over displayda m }$

이것들은 우리 시스템을 지배하는 기본 방정식을 나타냅니다.

파라미터화된 클럭과 진자 시스템의 경우 t $\displaystyle$ t가 $t$ 독립 변수인 $t$ 인 운동 방정식을 복구할 수 있습니다.

$dx/dt$ 서 $dx/dt$ d $dx/dt$ / $dx/dt$ t { $displaystyle dx$ / $dx/dt$ $dp/dt$ } $dp/dt$ d p $dp/dt$ / d t { $displaystyle dp$ / dt $dp/dt$ }는 $dp/dt$ 다음과 같이 추론할 수 있습니다.

${displaystyle {display\over dt}={\Big /}{dt \over d\display }={displayda p/m \over \displayda }={p \over m}$

${dp \over dt}={\Big /}{dt \over d\big }={-\bigda m\obe ^{2}x \over \bigda }=-m\obe ^{2}x$

단순 고조파 발진기에 대한 일반적인 미분 방정식을 복구합니다.

${displaystyle {d^2}x \over dt^{2}}=-\opega ^{2}x.}$

$또한$ $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ p $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ / $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ p t / $d$ / d / / d $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ / $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ = $=$ $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ \ $display$ $style dp$ _ { t } / $dp$ _ { t } / $dp$ _ { t } / $d\ display$ style p $_$ { $t$ $0$ $dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0$ $p_{t}=Const.$ d d d d $p_{t}=Const.$ $=$ C $p_{t}=Const.$ d d we we we we we we we we we we we we we we we we we $p_{t}=Const.$ we we we we we we we we we we we we we we we we we we we we we we we we we we we we we we we we we we we we $}$

그러면 우리의 해밀턴 제약은 에너지의 항상성 상태로 쉽게 볼 수 있습니다!탈파라메트리제이션과 모든 것이 진화하는 시간 변수의 식별은 파라메트리제이션의 반대 과정이다.일반적으로 모든 재매개 불변 시스템이 비매개체화될 수 있는 것은 아닌 것으로 밝혀졌다.일반상대성이론은 대표적인 물리적인 예다(여기서 시공간 좌표는 비물리적인 $\tau$ 에 대응하며 해밀턴식은 공간 및 시차 동형을 생성하는 구속조건의 선형 조합이다).

왜 우리가 여기서 배우자를 제거할 수 있었는지

(애초에 인위적인 재자극이었다는 사실을 이미 알고 있다는 사실과는 별도로) 우리가 탈자극할 수 있었던 근본적인 이유는 제약의 수학적 형태이다. 즉,

$C=p_{t}+C'(x,p)$ $C=p_{t}+C'(x,p)$ $C=p_{t}+C'(x,p)$ t + $C=p_{t}+C'(x,p)$ $C=p_{t}+C'(x,p)$ ( $C=p_{t}+C'(x,p)$ , $C=p_{t}+C'(x,p)$ ){ $displaystyle$ C $=p_{t}+C'(x,p$

해밀턴 구속조건을 원래 작용으로 대체한다.

$S=\int d\big [}{big \over d\big }p+{dt \over d\big }p_{t}-\bigda (p_{t}+C'(x,p){\big }}$

$=\int d\big {\big [ }p-{dt \over d\big }C'(x,p){\Big }}$

$\displaystyle =\int dtpn큰 [}{dx \over dt}p-{p^{2} \over 2m}+{1 \over 2}m\Omega ^{2}x^{2}{\Big ]}$

이것은 고조파 발진기의 표준 동작입니다.일반상대성이론은 해밀턴 제약조건이 일반적으로 위의 수학적 형태가 아닌 물리 이론의 한 예이며, 따라서 일반적으로는 비캐러메트릭화될 수 없습니다.

해밀턴 고전 일반 상대성 이론

일반 상대성 이론의 ADM 공식에서 시공간을 공간 슬라이스와 시간으로 분할할 때, 기본 변수는 공간 슬라이스(시공간 메트릭에 의해 공간 슬라이스에 유도되는 메트릭)의 유도 메트릭 $q_{ab}(x)$ a ( $x)$ style $q_{ab}(x)$ 와 $q_{ab}(x)$ 외연과 관련된 그것의 공역 운동량 변수이다.c 곡률, $K^{ab}(x)$ $K^{ab}(x)$ b ( $K^{ab}(x)$ ) { $displaystyle$ K $^{ab}(x$ (이는 공간 슬라이스가 시공간과 관련하여 어떻게 곡선을 그리며 유도 메트릭이 시간에 어떻게 ^[1]진화하는지를 나타내는 척도입니다.)이것들은 미터법 표준 좌표입니다.

필드의 시간 진화와 같은 역학은 해밀턴 제약에 의해 제어된다.

해밀턴 제약 조건의 정체는 양자 중력의 주요 미해결 문제이며, 그러한 특정 제약 조건으로부터 물리적 관측 가능성의 추출도 마찬가지이다.

1986년 Abhay Ashtekar는 SU(2) 게이지 장과 그 보완 ^[2]변수의 관점에서 3차원 공간 슬라이스에 미터법 표준 변수를 다시 쓰는 특이한 방법을 나타내기 위해 새로운 표준 변수 세트인 Ashtekar 변수를 도입했다.해밀턴족은 이 개혁에서 훨씬 단순화되었다.이것은 양자 일반 상대성^[3] 이론의 루프 표현으로 이어졌고 결과적으로 양자 중력의 루프 표현으로 이어졌다.

루프 양자 중력 표현 내에서 티만은 수학적으로 엄격한 연산자를 그러한 제약 ^[4]조건으로서 제안으로 공식화했다.비록 이 연산자가 완전하고 일관성 있는 양자 이론을 정의하지만, 고전적인 일반 상대성 이론과의 불일치로 인해 이 이론의 물리적 실체에 대한 의문이 제기되었다. (양자 제약 대수는 닫히지만, 그것은 i의 정황 증거로 보여지는 GR의 고전 제약 대수와 동형이 아니다.)불일치의 증거는 결코 아니다) 등 다양한 방법이 제안되고 있습니다.

미터법 공식화

아이디어는 표준 $q_{ab}$ $q_{ab}$ a $(\$ 및 $q_{ab}$ $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ a $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ $=$ ( $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ b - $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ $\pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})$ $){displaystyle \pi$ ^{ $ab$ }= $sqrt {q}}(K^{ab}-q^{c}^{c$ 를 계량화하여 연산자로 만드는 것이었다.스트레인)그러나, 이 프로그램은 곧 여러 가지 이유로 인해 위압적으로 어려워졌습니다. 하나는 해밀턴 제약 조건의 비다항적 특성입니다.

${{displaystyle H=sqrt {det(q)}}(K_{ab}-(K_{a}^{a})^{2}-{}^{3}R)}$

$\;^{3}R$ 서 3 R $({displaystyle \;^{$ $3}$ $R)$ 은 $\;^3R$ 3가지 $q_{ab}(x)$ $q$ $(x$ 의 스칼라 곡률입니다. 정규 변수와 그 파생 변수에서 비다항식 표현이므로 양자 연산자로 승격하는 것은 매우 어렵습니다.

Ashtekar 변수를 사용한 식

Ashtekar 변수의 구성 변수는 $SU(2)$ U $SU(2)$ 2 $) 게이지$ 필드 또는 $A_{a}^{i}$ $A_{a}^{i}$ ({ $displaystyle A_{a}^i$ 와 $SU(2)$ 같이 동작합니다.규범적으로 공역하는 ${\tilde {E}}_{i}^{a}$ 은 E $~i(\displaystyle {E}_{i}^{$ a ${\tilde {E}}_{i}^{a}$ })입니다. 조밀화된 "전기" 필드입니다. ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ ~ ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ a ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ ( ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ ) ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ i ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ a ${\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}$ （ \ $displaystyle$ { $E } _$ { $i$ }^{ a } = $sqrt { det$ ( $q$ ) } $E$ _ { $i$ }^ $a$ } 。이 변수들이 중력과 무슨 관계가 있을까요?조밀화된 삼합회는 다음을 통해 공간 메트릭을 재구성하는 데 사용될 수 있습니다.

$det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ t $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ ( $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ q ) $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ b $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ ~ $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ E ~ $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ b $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ $det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}$ j { $displaystyle$ det ( $q$ ) ^ { $ab$ } = $tilde { E$ } $_$ { $i }$ { \ $tilde$ { $E$ } $_$ { $j$ } { b } \ $delta$ ^ { $ij$ }

고밀도 삼합회로는 고유하지 않으며, 실제로 내부 $지수$ 에 대해 공간 회전을 로컬로 수행할 수 $있습니다$ 이것이 실제로 $)\displaystyle$ SU( $2)$ $SU(2)$ 불변성의 원인입니다.연결을 사용하여 외부 곡률을 재구성할 수 있습니다.그 관계는 다음과 같다.

$A_{a}^{i}=\Gamma_{a}^i}-iK_{a}^{i$

여기서 $\Gamma _{a}^{i}$ $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ $\Gamma _{a}^{i}$ \ $displaystyle$ \ $Gamma _$ { $a }^{$ $displaystyle$ \ $Gamma$ _ $\Gamma _{a}^{i}$ { a \ ; $i$ }^{ a $\Gamma _{a\;\;i}^{\;\;j}$ $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ $\Gamma _{a\;\;i}^{\;\;j}$ $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ k $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ $\Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}$ $（$ $display$ style \ $Gama$ }^{ a }^{ a } $\Gamma _{a\;\;i}^{\;\;j}$ $where$ a = where $\Gamma _{a\;\;i}^{\;\;j}$ where where where ϵ a k where k 、 \ displaystyle \ $Gamma$ }^{ display style \ Gamma }^{ damma }^{ displaysty $aystyle$ K_ ${a}^{i}=K_{ab}{\tilde {E}}^ai}/{\sqrt {det(q$

Ashtekar 변수의 관점에서 제약조건의 고전적 표현은 다음과 같다.

$H={\epsilon _{ijk}F_{ab}^{k}{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b} \over {\sqrt {det(q)}}}$ $F_{ab}^{k}{\tilde {E}_{i}^a}{\tilde {E}}_{j}^b}\over {sqrt {det(q$

$F_{ab}^{k}$ 서 $F_{ab}^{k}$ $A_{a}^{i}$ $A_{a}^{i}$ 의 F $F_{ab}^{k}$ {\ $displaystyle F_{ab}{k}{$ $i}{$ displaystyle $A_{a}{i$ }}}의 $F_{ab}^{k}$ 필드 강도 텐서. $1/{\sqrt {det(q)}}$ / $1/{\sqrt {det(q)}}$ $1/{\sqrt {det(q)}}$ ( $1/{\sqrt {det(q)}}$ q $1/{\sqrt {det(q)}}$ ) { $displaystyle$ 1/{\ $sqrt {det($ q)}}로 $1/{\sqrt {det(q)}}$ 인해 Ashtekar 변수에서 이는 비다항식이 된다.우리가 조건을 부과했으니까

$H=0$ $H=0$ $(디스플레이 스타일$ H $=0$

대신 조밀화된 해밀턴을 고려할 수 있습니다.

${\tilde {H}}={\sqrt {det(q)}}H=\epsilon _{ijk}F_{ab}^{k}{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}=0$ $}H=\epsilon_{ijk}$ $F_{ab}^{k}{\tilde {E}_{i}^a}{\tilde {E}_{j}^b}=0$

이 해밀턴식은 이제 아슈테카의 변수들 다항식이 된다.이 개발은 표준 양자 중력 ^[5]프로그램에 대한 새로운 희망을 불러일으켰다.아슈테카 변수는 해밀턴을 단순화하는 장점이 있었지만 변수가 복잡해진다는 문제가 있다.이론을 양자화할 때 복잡한 일반상대성이론과 반대로 실제 일반상대성이론을 회복하는 것은 어려운 일이다.또한 조밀화된 해밀턴을 양자 연산자로 승격시키는 데에도 심각한 어려움이 있었다.

현실 조건의 문제를 해결하는 방법은 로렌츠 대신 $(+,+,+,+)$ $(+,+,+,+)$ $(+,+,+,+)$ $(\displaystyle$ 로 서명을 $(+,+,+,+)$ 취하면 해밀턴의 단순한 형식을 그대로 유지할 수 있지만 실제 변수를 위해 사용할 수 있다는 점에 주목하는 것이었습니다.그런 다음 로렌츠 이론을 회복하기 위해 일반화 윅 회전이라고 불리는 ^[6]것을 정의할 수 있습니다.위상공간의 Wick 변환이며 시간 $파라미터$ t $\displaystyle$ t의 분석적 연속과는 무관하므로 일반화됩니다.

Ashtekar 변수의 실제 공식화를 위한 표현

Thomas Tiemann은 위의 ^[4]두 가지 문제를 모두 해결했다.그는 진짜 연줄을 이용했다.

$A_{a}^{i}=\Gamma_{a}^i}+\display K_{a}^{i$

실제 아슈테카 변수에서 해밀턴의 전체는

$H=-\zeta {\epsilon _{ijk}F_{ab}^{k}{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b} \over {\sqrt {det(q)}}}+2{\zeta \beta ^{2}-1 \over \beta ^{2}}{({\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}-{\tilde {E}}_{j}^{a}{\tilde {E}}_{i}^{b}) \over {\sqrt {det(q)}}}(A_{a}^{i}-\Gamma _{a}^{i})(A_{b}^{j}-\Gamma _{b}^{j})=H_{E}+H'$ $_lon {ijk}$ $F_{ab}^{k}{\tilde {E}_{i}^{a}{\tilde {E}_{j}^{b}\over {\tilde {det(q)}}+2'zeta \over ^{2}-1 \over ^{2}}{{(\tilde {E}_i} {j}}} {tilde}$ $H_{E}+H$

$\beta$ 서 상수 $\beta$ β(\ $displaystyle \beta)$ 는 $\beta$ Barbero-Imirzi 파라미터입니다.^[7]상수 $\zeta$ (\ $displaystyle \zeta)$ 는 $\zeta$ 로렌츠 시그니처의 경우 -1, 유클리드 시그니처의 경우 +1입니다. $\Gamma _{a}^{i}$ $\Gamma _{a}^{i}$ style _ $Gamma$ _ {a }^{ $i}$ 는 $\Gamma _{a}^{i}$ 밀도가 높은 삼합체와 복잡한 관계를 가지며 양자화 시 심각한 문제를 일으킨다.Ashtekar 변수는 두 번째 더 복잡한 항을 사라지게 하기 위해 $\beta =i$ $= i를$ 한 $\beta = i$ 것으로 볼 수 있다 $(유클리드$ 이론의 경우 이 항은 β $=$ ± $(\displaystyle \display$ =\ $pm$ 1) $\beta =\pm 1$ 의 $\beta =\pm 1$ 선택에 대해 남아있기 때문에 첫 번째 항은 $(\$ })로 $H_E$ 표기된다).또한 $1/{\sqrt {det(q)}}$ 1/ $1/{\sqrt {det(q)}}$ e $1/{\sqrt {det(q)}}$ ( $1/{\sqrt {det(q)}}$ ) { $displaystyle$ 1 $/{\sqrt {det(q)}}$ 계수의 $1/{\sqrt {det(q)}}$ 문제도 남아 있습니다.

Tiemann은 $\beta$ β(\ $displaystyle$ $\beta$ 에 대해 작동시킬 수 있었다. 먼저 그는 식별자를 사용하여 $1/{\sqrt {det(q)}}$ 아픈 $1/{\sqrt {det(q)}}$ / $d$ e t ( $1/{\sqrt {det(q)}}$ {displaystyle 1 $/{\sqrt {det(q)}}$ 을 $1 / \sqrt{det (q)}$ 단순화할 수 있었다.

${\displaystyle \{A_{c}^{k},V\}= epsilon ^{ijk}{\tilde {E}^{a}{\tilde {E}}_{j}^{b}\over {rt {det(q)}}}}.$

$V$ 서 V $(\displaystyle$ V $)$ 는 $V$ 볼륨입니다.

$V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ e $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ ( $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ ) $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ x E ~ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ a $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ E ~ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ E ~ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ c $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ k $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ $V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}$ c { $display style$ V =\ $int$ d $^{3}xcrt {$ det (q ) } $=$ { 1 \ $over 6 }$ $\int$ d^ { $trt}$

해밀턴 제약 조건의 첫 번째 항은

$H_{E}=\{A_{c}^{k},V\}F_{ab}^{k}{\tilde{epsilon}}^{abc$

티만의 신분을 이용했을 때요이 포아송 괄호는 양자화 시 정류자로 대체됩니다.비슷한 수법이 두 번째 학기를 가르치는데 사용될 수 있다는 것이 밝혀졌습니다.Why are the $\Gamma _{a}^{i}$ given by the densitized triads ${\tilde {E}}_{i}^{a}$ ? It actually come about from the Gauss Law

$D_{a}{\tilde {E}}_{i}^{a}=0$ $D_{a}{\tilde {E}}_{i}^{a}=0$ E ~ $D_{a}{\tilde {E}}_{i}^{a}=0$ a $=$ (\ $displaystyle D_{a}{\tilde {E}}_{i}^{a$ }= $0$

다양한 인덱스를 회전시킨 후 더하기 및 빼기 작업을 통해 방정식 $\nabla _{c}g_{ab}=0$ $\nabla _{c}g_{ab}=0$ g $\nabla _{c}g_{ab}=0$ $\nabla _{c}g_{ab}=0$ $=$ 0 { $displaystyle$ \ $subla$ _ { $c$ } $g$ _ { ab } $= 0$ 에서 계산할 수 있는 것과 거의 동일한 방법으로 이 문제를 해결할 수 있습니다.결과는 복잡하고 비선형적입니다.이 복잡한 관계에 의해 야기된 문제들을 피하기 위해 티만은 먼저 가우스 게이지 불변량을 정의한다.

$K=\int d^{3}xK_{a}^{i}{\tilde {E}_{i}^{a}$

$K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ 서 K $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ b $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ ~ $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ / $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ e $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ ( $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ ) { $displaystyle K$ _ { $a$ }^{ $i } = K$ _ { $ab$ } { \ $tilde$ { E } } / { \ sqrt { det ( $q$ ) $K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}$ 。

$K_{a}^{i}=\{A_{a}^{i},K\}$ $K_{a}^{i}=\{A_{a}^{i},K\}$ i $=$ { $K_{a}^{i}=\{A_{a}^{i},K\}$ $K_{a}^{i}=\{A_{a}^{i},K\}$ i , $K_{a}^{i}=\{A_{a}^{i},K\}$ $}$ { $displaystyle K_{a}^{i$ }=\{ $A_{a}^{i},K$

그러면 우리는 글을 쓸 수 있다.

$({displaystyle A_{a}^{i}-\Gamma _{a}^i}=\beta \{A_{a}^{i},K\})$

설정 $A_{a}^{i}$ $A_{a}^{i}$ $(\$ $및$ K $(\displaystyle$ K $K$ 의 $A_{a}^{i}$ 관점에서 식을 찾습니다. 우리는 해밀턴의 두 번째 항에 대해 구합니다.

$}$ $A_{a}^{i},K\}\{A_{b}^{j},K\}\{A_{c}^{k},V$

왜 $K$ 를 $K$ 하는 것이 더 쉬운가? 이는 우리가 이미 계량화 방법을 알고 있는 수량으로 다시 쓸 수 있기 때문입니다. $K$ 으로 K $(\displaystyle$ K $)$ 는 $K$ 다음과 같이 고쳐 쓸 수 있습니다.

$\displaystyle K=-\{V,\int d^{3}xH_{E}\}}$

여기서 우리는 외인성 곡률의 통합된 밀도화 트레이스를 "부피의 시간 미분"이라고 사용했다.

레퍼런스

^ 중력: 찰스 W. 미스너, 킵 S.Thorne, John Archibald Wheeler, W. H. Freeman and company에 의해 출판되었습니다.뉴욕.
^ Ashtekar, Abhay (1986-11-03). "New Variables for Classical and Quantum Gravity". Physical Review Letters. American Physical Society (APS). 57 (18): 2244–2247. doi:10.1103/physrevlett.57.2244. ISSN 0031-9007.
^ Rovelli, Carlo; Smolin, Lee (1988-09-05). "Knot Theory and Quantum Gravity". Physical Review Letters. American Physical Society (APS). 61 (10): 1155–1158. doi:10.1103/physrevlett.61.1155. ISSN 0031-9007.
^ ^a ^b Thiemann, T. (1996). "Anomaly-free formulation of non-perturbative, four-dimensional Lorentzian quantum gravity". Physics Letters B. Elsevier BV. 380 (3–4): 257–264. arXiv:gr-qc/9606088. doi:10.1016/0370-2693(96)00532-1. ISSN 0370-2693.
^ 이에 대한 자세한 내용과 후속 개발에 대한 자세한 내용은 책 "비강동 정준중력 강의"를 참조하십시오.1991년 초판.세계 과학 출판사특수부대원.
^ Thiemann, T (1996-06-01). "Reality conditions inducing transforms for quantum gauge field theory and quantum gravity". Classical and Quantum Gravity. IOP Publishing. 13 (6): 1383–1403. arXiv:gr-qc/9511057. doi:10.1088/0264-9381/13/6/012. ISSN 0264-9381.
^ Barbero G., J. Fernando (1995-05-15). "Real Ashtekar variables for Lorentzian signature space-times". Physical Review D. American Physical Society (APS). 51 (10): 5507–5510. arXiv:gr-qc/9410014. doi:10.1103/physrevd.51.5507. ISSN 0556-2821.

외부 링크

[1] 중력: 찰스 W. 미스너, 킵 S.Thorne, John Archibald Wheeler, W. H. Freeman and company에 의해 출판되었습니다.뉴욕.

[2] Ashtekar, Abhay (1986-11-03). "New Variables for Classical and Quantum Gravity". Physical Review Letters. American Physical Society (APS). 57 (18): 2244–2247. doi:10.1103/physrevlett.57.2244. ISSN 0031-9007.

[3] Rovelli, Carlo; Smolin, Lee (1988-09-05). "Knot Theory and Quantum Gravity". Physical Review Letters. American Physical Society (APS). 61 (10): 1155–1158. doi:10.1103/physrevlett.61.1155. ISSN 0031-9007.

[Thiemann-4] Thiemann, T. (1996). "Anomaly-free formulation of non-perturbative, four-dimensional Lorentzian quantum gravity". Physics Letters B. Elsevier BV. 380 (3–4): 257–264. arXiv:gr-qc/9606088. doi:10.1016/0370-2693(96)00532-1. ISSN 0370-2693.

[5] 이에 대한 자세한 내용과 후속 개발에 대한 자세한 내용은 책 "비강동 정준중력 강의"를 참조하십시오.1991년 초판.세계 과학 출판사특수부대원.

[6] Thiemann, T (1996-06-01). "Reality conditions inducing transforms for quantum gauge field theory and quantum gravity". Classical and Quantum Gravity. IOP Publishing. 13 (6): 1383–1403. arXiv:gr-qc/9511057. doi:10.1088/0264-9381/13/6/012. ISSN 0264-9381.

[7] Barbero G., J. Fernando (1995-05-15). "Real Ashtekar variables for Lorentzian signature space-times". Physical Review D. American Physical Society (APS). 51 (10): 5507–5510. arXiv:gr-qc/9410014. doi:10.1103/physrevd.51.5507. ISSN 0556-2821.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Search