그라데이션 네트워크

이 기사는 주요 출처에 대한 언급에 너무 많이 의존하고 있다. 2차 또는 3차 소스를 추가하여 개선하십시오.(2021년 10월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

이 글은 독자들에게 혼란스럽거나 불명확할 수 있다. 기사에 대해 명확하게 설명할 수 있도록 도와주십시오. 토크 페이지에서 이에 대한 논의가 있을 수 있다(2021년 10월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

네트워크 과학에서, 그라데이션 네트워크는 각 노드가 관련된 스칼라 잠재력과 그 근방에서 가장 작은(또는 가장 큰) 잠재력을 가진 노드를 가리키는 하나의 아웃링크를 갖는 간접되지 않은 "하향된" 네트워크의 방향 하위 네트워크로, 기판 네트워크에서 자신과 그 이웃의 결합으로 정의된다.^[1]

정의

전송은 기판 그래프라 불리는$$ 고정 $네트워크{\displaystyle }$ G${\displaystyle }$= ${\displaystyle G}$(${\displaystyle V}$, $){\displaystyle G=G(V,E)}$에서 이루어진다.It has N nodes, ${\displaystyle V=\{0,1,...,N-1\}}$ and the set of edges ${\displaystyle E=\{(i,j) i,j\in V\}}$. Given a node i, we can define its set of neighbors in G by S_i⁽¹⁾ = {j ∈ V (i,j)∈ E}.

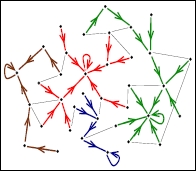
또한 노드 V 집합에 정의된 스칼라 필드 h = {h₀, ..h_N−1}을(를) 고려하여 모든 노드 I에 연결된 스칼라 값 h를_i 갖도록 합시다.

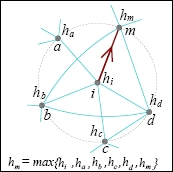
Gradient ∇h_i on a network: ∇h_i${\displaystyle =}$(i, μ(i)) i.e. the directed edge from i to μ(i), where μ(i) ∈ S_i⁽¹⁾ ∪ {i}, and h_μ has the maximum value in ${\displaystyle {h_{j} j\in S_{i}^{(1)}\cup {i}}}$.

그라데이션 네트워크: ∇ ${\displaystyle }$= ${\displaystyle$ ${\displaystyle }$$=}$ ∇$$ G ${\displaystyle$ G$\}($${\displaystyle V}$,${\displaystyle F}$) ${\displaystyle(V,F)},$ 여기서$$ F는 G의 그라데이션 에지 집합이다.

일반적으로 스칼라 장은 네트워크의 흐름, 외부 소스 및 싱크 때문에 시간에 따라 달라진다.따라서 그라데이션 ${\displaystyle }$ ∇ G ${\displaystyle G}$은(는) 동적으로 된다$$.^[3]

동기부여와 역사

그라데이션 네트워크의 개념은 토로츠카이와 바슬러(2004)에 의해 처음 도입되었다.^[4][5]

일반적으로 정보, 자동차, 전력, 물, 힘 등 운송 주체로 진화하는 경우가 많은 실세계 네트워크(인용 그래프, 인터넷, 세포 대사 네트워크, 세계 공항 네트워크 등)는 세계적으로 설계되지 않고 오히려 지역적 변화를 통해 진화하고 성장한다.예를 들어, 인터넷상의 라우터가 자주 혼잡하고 그로 인해 패킷이 손실되거나 지연된다면, 그것은 여러 개의 상호 연결된 새로운 라우터로 대체될 것이다.^[2]

더욱이 이 흐름은 종종 스칼라의 국부적인 구배들에 의해 생성되거나 영향을 받는다.예를 들어, 전류의 경사로가 전류를 구동한다.정보망에서 노드의 속성은 노드에서 이웃으로 정보가 전달되는 방식에 편향을 일으킬 것이다.이러한 생각은 흐름이 네트워크에 분산된 스칼라장의 경사로 인해 구동되는 경우 그라데이션 네트워크를 이용하여 네트워크의 흐름 효율을 연구하기 위한 접근방식의 동기를 부여했다.^[2][3]

최근의 연구는^{[which?][needs update]} 네트워크 토폴로지와 교통의 흐름 효율성 사이의 연관성을 조사한다.^[2]

그라데이션 네트워크의 수준별 분포

그라데이션 네트워크에서, node i, k의_i 인도는 i를 가리키는 그라데이션 에지의 수입니다. 인도 분포는 $R{\displaystyle }$ (${\displaystyle l}$)${\displaystyle }$= ${\displaystyle P}${ ${\displaystyle k_{}^{}}$ ${\displaystyle {}_{}^{}}$( ${\displaystyle i_{}^{}}$ n${\displaystyle {}_{}^{}}$)${\displaystyle {}_{}^{}}$= ${\displaystyle l}$ ${\displaystyle \}}$ = l $}$ {\$displaystyle$ R$(l)=$이다.$P\{k_{i}^{(in)}=l\}}}}.$

기질 G가 랜덤 그래프이고 각 노드 쌍이 확률 P(즉, Erdds-Rényi 랜덤 그래프)와 연결되면 스칼라 h는_i I.i.d.(독립적으로 동일한 분포) R(l)에 대한 정확한 표현은 다음과 같다.

${\displaystyle R(l)={\frac {1}{N}\sum _{n-1}^{{n-1-n}[1-p(1-p)]^{N-1-n-l}[1-p)^{n-l}^{n-l}}}$^[3]

$한계{\displaystyle }$N → ${\displaystyle \mathrm{\infty }}$ ${\displaystyle N\to \infit }$ 및 $P$ → ${\displaystyle 0}$ ${\displaystyle P\to 0}$에서 도 분포는 전력 법칙이 된다$.$

${\displaystyle R(l)\ 근사치 l^{-1}$

이것은 이 제한에서 랜덤 네트워크의 그라데이션 네트워크는 무스케일임을 보여준다.^[3]

더욱이, 기판 네트워크 G가 바라바시-알버트 모델에서와 같이 스케일 프리인 경우, 그라데이션 네트워크도 G의 지수와 동일한 지수를 갖는 파워 로우를 따른다.^[2]

네트워크의 정체

기판 네트워크의 토폴로지가 네트워크 혼잡도에 영향을 미친다는 사실은 단순한 예로 설명될 수 있다: 만일 네트워크가 별과 같은 구조를 가지고 있다면, 그렇다면 중앙 노드에서 다른 노드에서 오는 모든 흐름을 중앙 노드가 처리해야 하기 때문에 흐름이 혼잡해질 것이다.그러나 네트워크에 고리 같은 구조가 있으면 모든 노드가 같은 역할을 하기 때문에 흐름 혼잡은 없다.

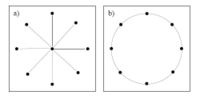
흐름이 네트워크의 구배들에 의해 생성된다고 가정할 때, 네트워크의 흐름 효율성은 다음과 같이 정의되는 방해 요인(또는 혼잡 요인)을 통해 특성화할 수 있다.

${\displaystyle J=1-\langle \langle \langle {N_{\text{recept}}{N_{\text{send}}\rangele _{h}\rangele _{\textnet}=R(0)}$

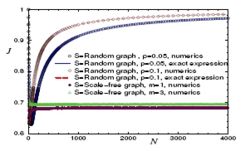
여기서 N은_receive 그라데이션 흐름을 받는 노드의 수이고 N은_send 그라데이션 흐름을 보내는 노드의 수입니다.J의 값은 0과 1 ${\displaystyle \mathrm{사이}}$에 있고,${\displaystyle }J{\displaystyle }$ = 0 ${\displaystyle$J=$0}$은 혼잡함이 없음을 의미하며$$, $J{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle J=1}$은 최대 혼잡에 해당한다$$.한계 $N{\displaystyle }$→ ${\displaystyle \mathrm{\infty }}$ ${\displaystyle N\to \infit }$에서$$Erdds-Rényi 랜덤 그래프의 경우 혼잡인자가 된다.

${\displaystyle J(N,P)=1-{\frac {\lnN}{N\{1-P}}}}}}}왼쪽[1+O({\frac {1}{N}})\오른쪽 화살표 1.}$

이 결과는 무작위 네트워크가 그 한도에서 최대 정체성을 보인다는 것을 보여준다.반대로, 스케일 프리 네트워크의 경우, J는 어떤 N에 대해서도 상수로서, 스케일 프리 네트워크는 최대 걸림돌을 일으키기 쉬운 경향이 없다는 것을 의미한다.^[6]

혼잡통제를 위한 접근방법

통신망의 한 가지 문제는 혼잡을 제어하고 정상적이고 효율적인 네트워크 기능을 유지하는 방법을 이해하는 것이다.^[7]

종화 류 외(2006)은 네트워크 수준이 높은 노드에서 정체가 발생할 가능성이 더 높다는 것을 보여주었으며, 소분수(예: 3%)의 노드의 메시지 처리 능력을 선택적으로 향상시키는 효율적인 접근방식은 모든 노드의 기능 향상과 마찬가지로 수행되는 것으로 나타났다.^[7]

Ana L Pastore y Pionti 등.(2008)은 이완 역학이^{[clarification needed]} 네트워크 정체를 줄일 수 있다는 것을 보여주었다.^[8]

Pan 외 연구진(2011)은 가장자리가 노드 전위차 사이의 스칼라 차이에 대한 힘의 가중치를 부여받는 체계에서 방해 특성을 연구했다.^{[9][clarification needed]}

니우와 판(2016년)은 그라데이션 분야와 로컬 네트워크 토폴로지의 상관관계를 도입해 혼잡을 줄일 수 있다는 것을 보여줬다.^{[10][clarification needed]}

참고 항목

• 네트워크 역학
• 네트워크 위상
• 양자복합망

참조