접기(고차 기능)
Fold (higher-order function)함수 프로그래밍에서 폴드(fold, reduced, accumulate, aggregate, compress 또는 inject라고도 함)는 재귀 데이터 구조를 분석하고 주어진 결합 연산을 사용하여 구성 요소를 재귀적으로 처리하여 반환값을 구축하는 고차 함수군을 말합니다.일반적으로 폴드는 결합함수, 데이터 구조의 상단 노드, 그리고 특정 조건에서 사용되는 일부 기본값과 함께 제공됩니다.그런 다음 접기는 함수를 체계적인 방식으로 사용하여 데이터 구조 계층의 요소를 결합합니다.
접힘은 전개에 대해 이중적인 의미로, 시드 값을 가져다가 코어 커시티브 데이터 구조를 점진적으로 구성하는 방법을 결정하기 위해 함수를 코어 커시티브하게 적용하는 반면, 접힘은 해당 구조를 재귀적으로 분해하여 각 노드에 결합 함수를 적용한 결과와 재귀적 결과(c)로 대체한다.무정형성 대 무정형성)이 전개됩니다.
구조적인 변화로서
이 섹션은 어떠한 출처도 인용하지 않습니다.(2013년 6월 (이 및 ) |
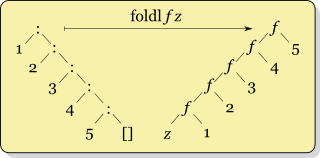
접힘은 데이터 구조의 구조 구성요소를 기능과 값으로 일관되게 대체하는 것으로 간주할 수 있습니다.예를 들어 리스트는 2개의 프리미티브에서 많은 기능언어로 작성됩니다.모든 리스트는 빈 리스트이며 보통 제로라고 불립니다.[] 또는 다른 목록 앞에 요소를 프리픽스하여 consnode(콘노드)라고 하는 것을 작성함으로써 구축됩니다. Cons(X1,Cons(X2,Cons(...(Cons(Xn,nil)))))의 적용에 의해 발생합니다.cons기능(대장으로서 기입)(:)(해스켈어로)목록의 접기는 목록의 끝에 있는 0을 특정 값으로 대체하고 각 항목을 특정 함수로 대체하는 것으로 볼 수 있습니다.이러한 교환은 다이어그램으로 볼 수 있습니다.
결합 함수에 공급될 때 각 노드의 두 링크 순서가 뒤집히는 일관된 방식으로 구조 변환을 수행하는 또 다른 방법이 있습니다.
이 그림들은 목록의 오른쪽과 왼쪽 접힌 부분을 시각적으로 보여줍니다.또, 이 점에서는,foldr (:) []cons를 lists의 ID 함수(리스프 용어로 얕은 복사)로 바꿉니다.cons이 전혀 없는nil결과는 변경되지 않습니다.왼쪽 접이식 다이어그램은 목록을 쉽게 되돌릴 수 있는 방법을 제시합니다.foldl (flip (:)) []추가할 요소가 결합 함수의 오른쪽 파라미터가 되므로 고려해야 할 파라미터는 플립해야 합니다.이 유리한 위치에서 쉽게 알 수 있는 또 다른 결과는 다음과 같은 관점에서 고차 맵 함수를 쓰는 것입니다.foldr를 사용하여 요소에 작용하는 기능을 구성함으로써cons, 다음과 같이 합니다.
지도 f = 폴더 ((:) . f) [] 여기서 마침표(.)는 함수 구성을 나타내는 연산자입니다.
이러한 관점에서 사물을 보는 것은 다양한 종류의 나무와 같은 다른 대수적 데이터 유형 및 구조에서 접힌 것과 같은 함수를 설계하는 간단한 경로를 제공합니다.데이터형 생성자를 제공된 함수로 재귀적으로 대체하고 유형의 상수 값을 제공된 값으로 대체하는 함수를 작성합니다.이러한 함수는 일반적으로 대격변이라고 불린다.
리스트 중
목록의 접기[1,2,3,4,5]덧셈 연산자를 사용하면 목록 요소의 합계가 15가 됩니다.[1,2,3,4,5]대략적으로 말하면, 이 접힘은 리스트의 콤마를 + 연산으로 대체하여 다음과 같이 하는 것으로 생각할 수 있다.1 + 2 + 3 + 4 + 5.
위의 예에서 +는 연관 연산이므로 최종 결과는 괄호에 관계없이 동일합니다.단, 구체적인 계산 방법은 다릅니다.비관련 이진 함수의 일반적인 경우 요소가 결합되는 순서가 최종 결과 값에 영향을 미칠 수 있습니다.목록에는 두 가지 분명한 방법이 있습니다. 첫 번째 요소를 나머지 요소를 재귀적으로 결합하는 결과(오른쪽 폴드라고 함)와 결합하거나 마지막 요소를 제외한 모든 요소를 재귀적으로 결합하는 결과(왼쪽 폴드라고 함)입니다.이것은 Haskell의 용어 또는 Prolog의 용어로 이진 연산자가 오른쪽 연결 또는 왼쪽 연결인 것에 해당합니다.오른쪽 접힘을 사용하면 합계는 다음과 같이 괄호 안에 넣을 수 있습니다.1 + (2 + (3 + (4 + 5)))반면 왼쪽 접기에서는 다음과 같이 괄호 안에 넣을 수 있습니다.(((1 + 2) + 3) + 4) + 5.
실제로 오른쪽 폴드의 경우 리스트의 끝에 도달했을 때 사용하고 왼쪽 폴드의 경우 리스트의 첫 번째 요소와 처음에 조합하는 초기값을 갖는 것이 편리하고 자연스러운 일이다.위의 예에서는 값 0(가법적 동일성)이 초기값으로 선택되어 다음과 같은 값을 얻을 수 있습니다.1 + (2 + (3 + (4 + (5 + 0))))적절한 접기, 그리고((((0 + 1) + 2) + 3) + 4) + 5왼쪽 접이식입니다.곱셈의 경우 초기 선택 항목 0은 작동하지 않습니다.0 * 1 * 2 * 3 * 4 * 5 = 0곱셈의 아이덴티티 요소는 1 입니다.이렇게 하면 우리가 얻을 수 있는 결과를 얻을 수 있을 것이다.1 * 1 * 2 * 3 * 4 * 5 = 120 = 5!.
선형 접힘과 트리 모양 접힘
결합 함수 f가 그 유형에서 비대칭일 때 초기 값을 사용해야 한다(예:a → b → b결과 유형이 목록 요소의 유형과 다른 경우).다음으로 어플리케이션의 선형 체인을 가능하게 하려면 f의 결과와 같은 타입의 초기값을 사용해야 합니다.좌향인지 우향인지 여부는 결합 함수에 의해 인수에서 예상되는 유형에 따라 결정됩니다.결과와 동일한 유형의 두 번째 인수인 경우 f는 오른쪽에 관련지어지는 바이너리 연산으로 볼 수 있으며 그 반대도 마찬가지입니다.
기능이 마그마인 경우, 즉 마그마의 유형이 대칭이다.a → a → a결과 유형은 목록 요소의 유형과 같으며 괄호는 임의의 방식으로 배치되어 중첩된 하위 표현 트리를 생성할 수 있습니다. 예를 들어, 다음과 같습니다.((1 + 2) + (3 + 4)) + 5이진법 연산 f가 연관성이 있는 경우, 이 값은 명확하게 정의됩니다.즉, 계산방법에 대한 자세한 내용은 다르지만 괄호 안에 대해서도 동일합니다.f가 엄격하지 않으면 효율에 큰 영향을 미칠 수 있습니다.
선형 접힘은 노드 지향이며 목록의 각 노드에 대해 일관된 방식으로 작동하는 반면, 트리 같은 접힘은 전체 목록 지향이며 노드 그룹 간에 일관된 방식으로 작동합니다.
비어 있지 않은 목록을 위한 특수 접기
연산 f의 아이덴티티 요소를 초기값 z로 선택하는 경우가 많습니다.예를 들어, 목록의 최대 요소를 얻기 위해 비어있지 않은 목록 위에 두 매개 변수 중 최대값을 계산하는 함수를 접고 싶을 때, 초기 값이 적절해 보이지 않을 때, 다음과 같은 변형이 있습니다.foldr그리고.foldl이 값은 목록의 마지막 요소와 첫 번째 요소를 각각 초기값으로 사용합니다.Haskell과 다른 몇몇 언어들에서는, 이러한 것들이라고 불린다.foldr1그리고.foldl1첫 번째 요소의 자동 프로비저닝을 참조하는1 및 해당 요소가 적용되는 목록에 적어도1개의 요소가 있어야 합니다.
이러한 접힘은 유형-대칭 이진 연산을 사용합니다. 인수와 결과의 유형은 동일해야 합니다.Richard Bird는 2010년 저서에서[1] "빈 목록이 아닌 목록의 일반적인 접기 함수"를 제안합니다.foldrn이것은 추가 인수 함수를 그것에 적용함으로써 폴딩을 시작하기 전에 결과 유형의 값으로 마지막 요소를 변환하고, 따라서 일반과 같은 유형-대칭 이진 연산을 사용할 수 있습니다.foldr목록의 요소 유형과 다른 유형의 결과를 생성합니다.
실행
선형 접힘
해스켈을 예로 들자면foldl그리고.foldr는 몇 가지 방정식으로 공식화할 수 있습니다.
접다 :: (b -> a -> b) -> b -> [a] -> b 접다 f z [] = z 접다 f z (x:xs) = 접다 f (f z x) xs 목록이 비어 있으면 결과가 초기값이 됩니다.그렇지 않은 경우 이전 초기값과 첫 번째 요소에 f를 적용한 결과를 새로운 초기값으로 사용하여 목록의 꼬리를 접습니다.
폴더 :: (a -> b -> b) -> b -> [a] -> b 폴더 f z [] = z 폴더 f z (x:xs) = f x (폴더 f z xs) 목록이 비어 있으면 초기 값 z가 됩니다.그렇지 않은 경우 첫 번째 요소와 나머지 요소를 접은 결과에 f를 적용한다.
나무와 같은 주름
리스트는 유한 리스트와 무한정의 리스트 양쪽에서 트리와 같은 방법으로 폴딩할 수 있습니다.
접다 f z [] = z 접다 f z [x] = f x z 접다 f z xs = 접다 f z (쌍들 f xs) 접다 f z [] = z 접다 f z (x:xs) = f x (접다 f z (쌍들 f xs)) 쌍들 f (x:y:t) = f x y : 쌍들 f t 쌍들 _ t = t 의 경우foldi무한히 정의된 목록에 대한 폭주 평가를 피하기 위해 함수f에서는 적어도 모든 인수 값을 요구하거나 즉시 요구해서는 안 됩니다(아래 예 참조).
목록이 비어 있지 않은 경우 접습니다.
접다 f [x] = x 접다 f (x:y:xs) = 접다 f (f x y : xs) 폴더1 f [x] = x 폴더1 f (x:xs) = f x (폴더1 f xs) 접다 f [x] = x 접다 f (x:y:xs) = 접다 f (f x y : 쌍들 f xs) 접다 f [x] = x 접다 f (x:xs) = f x (접다 f (쌍들 f xs)) 평가 오더 고려 사항
게으르거나 엄격하지 않은 평가가 있는 경우foldrf의 적용을 목록 선두에 즉시 반환하고 목록의 나머지 부분을 폴딩하는 재귀적 사례를 반환합니다.따라서, 만약 f가 그것의 "오른쪽"에 있는 재귀적 경우를 참조하지 않고 결과의 일부를 생산할 수 있고, 그리고 그 나머지 결과는 결코 요구되지 않는다면, 재귀는 멈출 것이다(예:head == foldr (\a b->a) (error "empty list")이렇게 하면 무한 목록에서 오른쪽 접기가 가능합니다.반대로foldl는 목록의 끝에 도달할 때까지 새로운 파라미터를 사용하여 즉시 자신을 호출합니다.이 테일 재귀는 루프로 효율적으로 컴파일할 수 있지만 무한 목록을 전혀 처리할 수 없습니다. 무한 루프에서 영원히 반복됩니다.
리스트의 끝에 도달하면 표현은 실제로 다음과 같이 작성됩니다.foldl네스트된 좌뇌의f- 어플리케이션.이러한 어플리케이션은 평가 대상 발신자에게 제시됩니다.함수는?f여기서 두 번째 인수를 먼저 참조하고 재귀 케이스(여기서 왼쪽의 첫 번째 인수)를 참조하지 않고 결과의 일부를 생성할 수 있도록 하면 재귀가 중지됩니다.즉, 이 말은foldr오른쪽에서 반복됩니다. 느린 결합 함수가 왼쪽에서 목록의 요소를 검사할 수 있습니다. 그리고 반대로,foldl왼쪽에서 반복됩니다. 느린 결합 함수가 목록 요소를 오른쪽에서 검사할 수 있습니다(예:last == foldl (\a b->b) (error "empty list")).
리스트의 반전도 테일리커시브입니다(이를 사용하여 구현할 수 있습니다).rev = foldl (\ys x -> x : ys) []유한 리스트에서는 왼쪽 폴드와 반대 폴드를 테일 리커시브 방식으로 실행할 수 있습니다(cf). 1+>(2+>(3+>0)) == ((0<+3)<+2)<+1기능 수정 포함)f즉, 논의의 순서를 뒤집는 것입니다(즉,foldr f z == foldl (flip f) z . foldl (flip (:)) []오른쪽 접이식 표현 표현 방식을 테일 어프로치 방식으로 구축합니다.외부 중간 목록 구조는 연속 통과 스타일 기법으로 제거할 수 있습니다.foldr f z xs == foldl (\k x-> k . f x) id xs z; 마찬가지로foldl f z xs == foldr (\x k-> k . flip f x) id xs z(flipHaskell과 같은 언어에서만 필요합니다. 그 결합 함수에 대한 논쟁의 뒤집힌 순서입니다.foldl예를 들어, 두 가지 기능을 결합하기 위해 동일한 순서로 인수가 사용되는 체계에서foldl그리고.foldr).
또 다른 테크니컬 포인트는 느린 평가를 사용하여 왼쪽 접기일 경우 재귀 호출이 이루어지기 전에 새로운 초기 파라미터가 평가되지 않는다는 것입니다.이로 인해 목록 끝에 도달하여 잠재적으로 거대한 표현식을 평가하려고 하면 스택 오버플로우가 발생할 수 있습니다.이러한 이유로, 이러한 언어들은 종종 재귀 호출을 하기 전에 초기 파라미터의 평가를 강제하는 더 엄격한 변형된 왼쪽 폴딩을 제공합니다.Haskell에서 이것은foldl'('prime'로 발음되는 아포스트로피'에 주의)의 함수는Data.List라이브러리(단, 느린 데이터 생성자를 사용하여 구축한 값을 강요하는 것은 자동으로 구성 요소를 강제하는 것은 아니라는 사실을 알아야 합니다).테일 재귀와 결합하면 이러한 접힘이 루프의 효율에 가까워져 최종 결과의 느린 평가가 불가능하거나 바람직하지 않은 경우 일정한 공간 작동이 보장됩니다.
예
Haskell 인터프리터를 사용하여 접기 함수가 수행하는 구조 변환을 문자열을 구성하여 설명할 수 있습니다.
λ> 폴더 (\x y -> 콘센트 ["(",x,"+",y,")"]) "0" (지도 보여 주 [1..13]) "(1+(2+(3+(4+(5+(6+(7+(8+(9+(10+(11+(12+(13+0)))))))))))))" λ> 접다 (\x y -> 콘센트 ["(",x,"+",y,")"]) "0" (지도 보여 주 [1..13]) "(((((((((((((0+1)+2)+3)+4)+5)+6)+7)+8)+9)+10)+11)+12)+13)" λ> 접다 (\x y -> 콘센트 ["(",x,"+",y,")"]) "0" (지도 보여 주 [1..13]) "(((((1+2)+(3+4))+((5+6)+(7+8)))+(((9+10)+(11+12))+13))+0)" λ> 접다 (\x y -> 콘센트 ["(",x,"+",y,")"]) "0" (지도 보여 주 [1..13]) "(1+((2+3)+(((4+5)+(6+7))+((((8+9)+(10+11))+(12+13))+0))))" 무한 트리 형태의 접힘은 예를 들어 하스켈의 에라토스테네스의 무한 체에 의한 재귀 소수 생산에서 입증된다.
소수점 = 2 : _Y ((3 :) . 마이너스 [5,7..] . 접다 (\(x:xs) ys -> x : 조합 xs ys) [] . 지도 (\p-> [p*p, p*p+2*p..])) _Y g = g (_Y g) -- = g.g.g.g.g.g... 여기서 함수는 로컬 방식으로 순서 목록에 대해 작동하여 집합 합집합과 집합 차이를 효율적으로 생성합니다.
소수점의 유한 접두사는 다음과 같이 열거된 정수 배수의 목록에 대한 집합 차분 연산의 접힘으로 간결하게 정의된다.
소수점 이하 n = 접다 마이너스 [[2*x,3*x..n] x <-> [1..n]] 예를 들어 병합 정렬(및 중복 제거 다양성)과 같은 유한 목록의 경우,nubsort)는 나무와 같은 접기를 사용하여 쉽게 정의할 수 있습니다.
머지소트 xs = 접다 합병하다 [] [[x] x <-> xs] 누브소트 xs = 접다 조합 [] [[x] x <-> xs] 중복 보존 변종 기능을 가진union.
기능들head그리고.last접힘을 통해 정의될 수 있었다
머리 = 폴더 (\x r -> x) (에러 "head: 빈 목록") 지난 = 접다 (\a x -> x) (에러 "마지막: 빈 목록") 다양한 언어로
| 언어 | 왼쪽 접이식 | 오른쪽 접이식 | 초기값이 없는 왼쪽 폴딩 | 초기값이 없는 오른쪽 폴딩 | 펼치다 | 메모들 |
|---|---|---|---|---|---|---|
| APL | func⍨/⌽initval,vector | func/vector,initval | func⍨/⌽vector | func/vector | ||
| C# 3.0 | ienum | ienum.Reverse() | ienum | ienum.Reverse() | Aggregate는 확장 방식입니다. ienum 은 IEnumerable<T>모두 마찬가지입니다.NET 언어 | |
| C++ | std::accumulate( | std::accumulate( | 머리글에<numeric>begin, end, redbegin, red는 반복자 func는 함수 포인터 또는 함수 객체일 수 있습니다. | |||
| C++17 | (initval op ... op pack) | (pack op ... op initval) | (... op pack) | (pack op ...) | Fold expression(변수 함수 템플릿의 경우에만): op은 바이너리 연산자입니다(두 ops가 동일해야 합니다).(std::cout << ... << args)), 팩은 전개되지 않은 파라미터 팩입니다. | |
| CFML | obj.reduce(func,initial) | obj.reduce(func) | 어디에func이전 조작의 결과를 인수로서 수신한다(또는initial첫 번째 반복 시 값); 현재 항목; 현재 항목의 색인 또는 키; 그리고 에 대한 참조obj | |||
| 클로쥬르 | (reduce func initval list) | (reduce func initval (reverse list')) | (reduce func list) | (reduce func" (reverse list)) | clojure.core.reducers/fold도 참조해 주세요. | |
| 일반적인 리스프 | (reduce func list :initial-value initval) | (reduce func list :from-end t :initial-value initval) | (reduce func list) | (reduce func list :from-end t) | ||
| 컬 | {{TreeNode.default treeNode ...} .to-Iterator} | {{TreeNode.default treeNode ...} .reverse} | {for {treeNode | {for {{treeNode.reverse} | 또한 DefaultListModel 및 HashTable 구현to-Iterator | |
| D | reduce!func(initval, list) | reduce!func(initval, list | reduce!func(list) | reduce!func( | 모듈로std.algorithm | |
| 엘릭시르 | List.foldl(list, acc, fun) | List.foldr(list, acc, fun) | 사용 예에 대해서는, 메뉴얼을 참조해 주세요. | |||
| 느릅나무 | List.foldl(Fun, Accumulator, List) | List.foldr(Fun, Accumulator, List) | 리스트 API도 참조해 주세요[ 1 ] | |||
| 얼랑 | lists:foldl(Fun, Accumulator, List) | lists:foldr(Fun, Accumulator, List) | ||||
| F# | Seq/List.fold func initval list | List.foldBack func list initval | Seq/List.reduce func list | List.reduceBack func list | Seq.unfold func initval | |
| 고수 | Iterable.fold(f(agg, e)) | 모두 Java의 Itherable 인터페이스 확장 방식이며 어레이도 지원됩니다. | ||||
| 그루비 | list | list.reverse() | list | list.reverse() | ||
| 하스켈 | foldl func initval list | foldr func initval list | foldl1 func list | foldr1 func list | unfoldr func initval | 폴딩의 경우 폴딩 함수는 폴딩의 경우와 반대 순서로 인수를 받아들인다. |
| Haxe | Lambda.fold(iterable, func, initval) | |||||
| J | verb~/ . initval,array | verb/ array,initval | verb~/ . array | verb/ array | u/y는 y 항목 사이에 dyad u를 적용합니다. "J 사전: 삽입" | |
| 자바 8 이상 | stream.reduce | stream.reduce | ||||
| 자바스크립트 1.8 ECMAScript 5 | array.reduce | array.reduce | ||||
| 줄리아. | foldl(op, itr; [init]) | foldr(op, itr; [init]) | foldl(op, itr) | foldr(op, itr) | ||
| 코틀린 | Iterable.fold | Iterable.foldRight | Iterable.reduce(func) | Iterable.reduceRight(func) | 다른 컬렉션도 지원fold[2] 그리고reduce.[3] 또 있습니다.Result.fold(onSuccess, onFailure)그 결과,[4]Result<T>(성공 또는 실패 중 어느 쪽이든) 반환 타입으로onSuccess그리고.onFailure. | |
| LFE | (lists:foldl func accum list) | (lists:foldr func accum list) | ||||
| 로그토크 | fold_left(Closure, Initial, List, Result) | fold_right(Closure, Initial, List, Result) | 메타 표준 라이브러리 개체에서 제공하는 메타 사전 인증서입니다.poldl 및 foldr의 약어도 사용할 수 있습니다. | |||
| 메이플 | foldl(func, initval, sequence) | foldr(func, initval, sequence) | ||||
| 매스매티카 | Fold[func, initval, list] | Fold[func, initval, Reverse[list]] | Fold[func, list] | Fold[func, Reverse[list]] | NestWhileList[func,, initval, predicate] | Fold초기값이 없는 경우 버전 10.0 이후에서는 지원됩니다. |
| 매트랩 | fold(@func, list, defaultVal) | fold(@func, flip(list), defaultVal) | fold(@func, list) | fold(@func, flip(list)) | | R2016b에서 지원되는 Symbolic Math Toolbox가 필요합니다. |
| 막시마 | lreduce(func, list, initval) | rreduce(func, list, initval) | lreduce(func, list) | rreduce(func, list) | ||
| 미스트릴 | fold_left func initval list | fold_right func initval list | 지정된 함수는 그 인수를 태플로 받아들입니다. | |||
| OCaml | List.fold_left func initval list | List.fold_right func list initval | Base.Sequence.unfold ~init ~f [5] | |||
| 오즈 | {FoldL List Func InitVal} | {FoldR List Func InitVal} | ||||
| PARI/GP | fold( f, A ) | |||||
| 펄 | reduce block initval, list | reduce block list | 에List::Util모듈 | |||
| PHP | array_reduce(array, func, initval) | array_reduce( | array_reduce(array, func) | array_reduce( | initval이 지정되지 않은 경우 NULL이 사용되므로 이것은 진정한 foldl1이 아닙니다.PHP 5.3 이전 버전에서는 initval은 정수만 사용할 수 있습니다."func"는 콜백입니다array_reduce online을 사용해 보겠습니다. | |
| 파이썬 2.x | reduce(func, list, initval) | reduce(lambda x,y: func(y,x), reversed(list), initval) | reduce(func, list) | reduce(lambda x,y: func(y,x), reversed(list)) | ||
| 파이썬 3.x | functools.reduce(func, list, initval) | functools.reduce(lambda x,y: func(y,x), reversed(list), initval) | functools.reduce(func, list) | functools.reduce(lambda x,y: func(y,x), reversed(list)) | 모듈 기능 도구.[6] | |
| R | Reduce(func, list, initval) | Reduce(func, list, initval, right=TRUE) | Reduce(func, list) | Reduce(func, list, right=TRUE) | R은 Reduce 함수에 대한 right 및 init 인수를 통해 초기값 유무에 관계없이 오른쪽 폴딩 및 왼쪽 또는 오른쪽 폴딩을 지원합니다. | |
| 루비 | enum | enum.reverse_each | enum | enum.reverse_each | Ruby 1.8.7+에서는 블록 대신 함수를 나타내는 기호를 전달할 수도 있습니다. enum은 열거형입니다. 이러한 오른쪽 접기 구현은 비교환 & 블록(초기값도 잘못된 쪽에 배치됨)에 대해 잘못된 것입니다. | |
| 녹 | iterator.fold(initval, func) | iterator.rev().fold(initval, func) | iterator.rev()필요.iterator가 되다DoubleEndedIterator를 클릭합니다.[7] | |||
| 스칼라 | list.foldLeft(initval)(func)(initval /: list)(func) | list.foldRight(initval)(func)(list :\ initval)(func) | list.reduceLeft(func) | list.reduceRight(func) | Scala의 상징적 접기 구문은 접기 [8]작업을 설명하기 위해 일반적으로 사용되는 왼쪽 또는 오른쪽 트리와 유사하도록 의도되었지만, 그 이후 쓰러지는 [9]도미노의 그림으로 재해석되었습니다.콜론은 일반적인 Scala 구문 메커니즘에서 유래합니다.이 메커니즘에서는 외관상의 infix 연산자가 왼쪽 오퍼랜드의 메서드로 호출되며 오른쪽 오퍼랜드가 인수로 전달됩니다.또한 콜론이 연산자의 마지막 문자일 경우 대칭적으로 적용됩니다. Scala는 또한 이 방법을 사용하여 나무와 같은 접힘을 특징으로 합니다. | |
| 스킴6 RRS | (fold-left func initval list) | (fold-right func initval list) | (reduce-left func defaultval list) | (reduce-right func defaultval list) | (unfold p f g seed [tail-gen])unfold-right p f g seed [tail](vector-unfold f length initial-seed ···)(vector-unfold-right f length initial-seed ···) | srfi/1 srfi/43 |
| 스몰토크 | aCollection inject: aValue into: aBlock | aCollection reduce: aBlock | ANSI Smalltalk는 #reduce:를 정의하지 않지만 많은 구현에서 정의됩니다. | |||
| 표준 ML | foldl func initval list | foldr func initval list | 지정된 함수는 그 인수를 태플로 받아들입니다.접힘의 경우 접힘 함수는 접힘 함수와 같은 순서로 인수를 받아들입니다. | |||
| 재빠르다 | array.reduce(initval, func) | array.reverse() | ||||
| XPath 3.1 | 배열: 왼쪽 폴더( $배열 ~하듯이 배열(*), $영 ~하듯이 아이템()*, $f ~하듯이 기능.( 아이템()*, 아이템()* } ~하듯이 아이템())* ) ~하듯이 아이템()* fn: 폴드 왼쪽( $인식하다 ~하듯이 아이템()*, $영 ~하듯이 아이템()*, $f ~하듯이 기능.( 아이템()*, 아이템() ) ~하듯이 아이템()* ) ~하듯이 아이템()* | 배열: 오른쪽 접기( $배열 ~하듯이 배열(*), $영 ~하듯이 아이템()*, $f ~하듯이 기능.( 아이템()*, 아이템()* } ~하듯이 아이템())* ) ~하듯이 아이템()* fn: 오른쪽 접기( $인식하다 ~하듯이 아이템()*, $영 ~하듯이 아이템()*, $f ~하듯이 기능.( 아이템(), 아이템()* ) ~하듯이 아이템()* ) ~하듯이 아이템()* | XPath 3.1에서는 과거의 이유로 인해array그리고.sequence타입이 호환되지 않습니다.따라서 다른 타입을 사용해야 합니다.fold기능array및 을 위해sequence
| |||
| Xtend | iterable.fold(initval,[func]) | iterable.reduce[func] |
유니버설리티
폴드는 다형 함수입니다.정의를 가진 모든 g에 대해
g [] = v g (x:xs) = f x (g xs) g는 다음과 같이 표현될[15] 수 있다.
g = 폴더 f v 또한 무한 리스트가 있는 게으른 언어에서는 [16]폴드를 통해 고정점 조합기를 구현할 수 있어 반복 횟수를 폴드로 줄일 수 있음을 증명합니다.
y f = 폴더 (\_ -> f) 정의되어 있지 않다 (따라하다 정의되어 있지 않다) 「 」를 참조해 주세요.
레퍼런스
- ^ Richard Bird, "기능 알고리즘 설계의 진주", 케임브리지 대학 출판부 2010, ISBN978-0-521-51338-8, 페이지 42
- ^ "fold - Kotlin Programming Language". Kotlin. Jetbrains. Retrieved 29 March 2019.
- ^ "reduce - Kotlin Programming Language". Kotlin. Jetbrains. Retrieved 29 March 2019.
- ^ "Result - Kotlin Programming Language". Kotlin. Jetbrains. Retrieved 29 March 2019.
- ^ "Base". Jane Street Capital. Retrieved February 26, 2019.
- ^ 참고용
functools.reduce:import functools
참고용reduce:from functools import reduce - ^ "Iterator in core::iter". Rust. Rust Team. Retrieved 2021-06-22.
- ^ Odersky, Martin (2008-01-05). "Re: Blog: My verdict on the Scala language". Newsgroup: comp.scala.lang. Retrieved 14 October 2013.
- ^ Sterling, Nicholas. "An intuitive feel for Scala's /: operator (foldLeft)". Retrieved 24 June 2016.
- ^ "Fold API - Scala Standard Library". www.scala-lang.org. Retrieved 2018-04-10.
- ^ 배열: 왼쪽 폴더
- ^ 왼쪽 접이식
- ^ 배열: 오른쪽 접기
- ^ 오른쪽 접기
- ^ Hutton, Graham. "A tutorial on the universality and expressiveness of fold" (PDF). Journal of Functional Programming (9 (4)): 355–372. Retrieved March 26, 2009.
- ^ Pope, Bernie. "Getting a Fix from the Right Fold" (PDF). The Monad.Reader (6): 5–16. Retrieved May 1, 2011.