엣지워스 상자

경제학에서 엣지워스 박스(Edgeworth-Bowley box)라고 불리기도 하는 엣지워스 박스는 X와 Y, 그리고 두 개의 소비자가 있는 시장을 그래픽으로 표현한 것이다. 상자의 치수는 두 상품의 총량 Ω과_x Ω이다_y.

소비자들은 옥타비오와 애비가 되게 하라. 상자의 오른쪽 상단 모서리는 옥타비오가 모든 상품을 보유하는 할당량을 나타내며, 왼쪽 하단에는 Abby의 완전한 소유권에 해당한다. 상자 안의 포인트는 두 소비자 사이에 상품을 배분하는 방법을 나타낸다.

시장의 행동은 소비자들의 무관심 곡선에 의해 결정될 것이다. 다이어그램의 파란색 곡선은 옥타비오에 대한 무관심 곡선을 나타내며, 그의 관점(즉, 왼쪽 아래에서 볼 수 있음)에서 볼록한 것으로 보인다. 오렌지색 곡선은 Abby에게 적용되며 오른쪽 위에서 볼 수 있듯이 볼록하다. 위와 오른쪽으로 움직이면 옥타비오의 할당이 늘어나고, 애비를 덜 바람직한 무관심 곡선에 놓이게 된다.

볼록한 무관심 곡선은 일반적인 경우로 간주된다. 그것들은 다른 상품에 비해 각각의 상품에 대한 수익 감소에 해당한다.

시장 내 교환은 기부로 알려진 최초 할당에서 시작된다.

엣지워스 박스의 주된 용도는 일반 평형 이론의 주제를 그래픽으로 시각화할 수 있는 형태로 도입하는 것이다. 양자 독과점 상황에서 효율적인 성과로 나아가는 어려움도 보여줄 수 있다.^[1] 후자의 경우 독특한 수치적 해법이 가능한 게임 이론의 협상 문제의 전구체 역할을 한다.^[2][3]

역사

엣지워스 박스 개발

엣지워스 상자는 프란시스 이즈드로 엣지워스의 이름을 따서 명명되었는데,^[4] 그는 이것을 그의 저서 Mathematical Sythics에서 발표했다. 수학의 도덕과학적 적용에 관한 논문, 1881년.^[5] 엣지워스의 원래 2축 묘사는 파레토가 1906년 정치경제 매뉴얼에서 현재 친숙한 박스 다이어그램으로 발전했고, 이후 보울리의 전시회에서 대중화되었다. 현대판 도표는 일반적으로 엣지워스-보울리 상자라고 불린다.^[6]

경제 평형의 수학적 이론

시장경제에서 평형의 개념체계는 레온 왈라스에^[7] 의해 개발되었고 빌프레도 파레토에 의해 더욱 확장되었다.^[8] 에이브러햄 월드,^[9] 폴 새뮤얼슨,^[10] 케네스 애로우, 제라드 데브레우 등 20세기 수학 경제학자들이 일반성과 엄격함에 대해 세심한 주의를 기울여 검토했다.^[11] 이것은 Wald가 또한 결정 이론에 더 엄격함을 가져오려고 노력했고 많은 수학자들은 선택의 공리에 대한 의존을 최소화하는데 집중했다.

왈라스 시장 이론은 주어진 결론을 얻을 수 있는 가장 일반적인 전제를 찾기 위해 애를 썼다. 전제가 강화되거나 약화될 수 있는 영역은 다음과 같다.

• 함수가 서로 다른지 여부.
• 무관심 곡선이 원시인지 효용 함수에서 파생되는지 여부
• 무관심 곡선이 볼록한지 여부.

가정은 또한 비반복성, 포화 등과 같은 보다 기술적인 성격으로 이루어진다.

엄격함을 추구하는 것이 항상 이해에 도움이 되는 것은 아니다. 이 글에서 무관심 곡선은 원시적인 것으로 취급될 것이다. 처음에는 볼록하고 차별성이 있는 것으로 간주하고 내부 평형주의에 집중하겠지만, 이후에는 이러한 가정들을 완화시킬 것이다.

시장균형

두 가지 상품만 있기 때문에 유효가격은 그들 사이의 환율이다. 우리의 목표는 시장 평형을 얻을 수 있는 가격을 찾는 것인데, 이는 주어진 기부금에서 출발하여 더 이상의 거래를 바라지 않는 지점이 될 것이다. 이러한 수량은 그림 2와 같이 두 소비자의 무관심 곡선에 의해 결정된다.

우리는 매일 옥타비오와 Abby가 다이어그램의 위치 Ω에 해당하는 두 상품에 대한 기부금(Ω_x, Ω_y )과 (Ω_x – Ω_x, Ω_y – Ω_y )을 가지고 시장에 간다고 가정한다. 그 두 소비자는 경쟁적인 시장 행동 하에서 그들끼리 교환할 것이다. 이러한 가정은 무한한 수의 소비자를 포함하는 완벽한 경쟁을 위한 조건이 충족되지 않기 때문에 일정한 불신의 정지를 필요로 한다.

만약 두 X의 교환이 하나의 Y로 이루어진다면, 옥타비오와 애비의 거래는 그들을 예산선으로 알려진 견고한 회색선을 따라 어느 지점까지 가져갈 것이다. (더 정확히 말하면, 예산선은 교환으로 얻을 수 있는 할당을 나타내는 기부 지점을 통과하는 직선으로 정의할 수 있다.) 몇 개의 다른 가격에 대한 예산 라인은 그림 2에서 점선과 점선으로 표시된다.

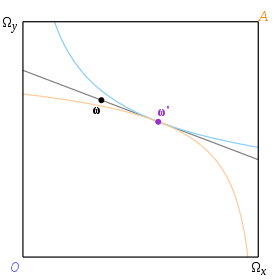
주어진 기부금 Ω에 해당하는 평형은 이 접선이 Ω을 통과하는 공통 접선을 갖는 무관심 곡선 쌍에 의해 결정된다. 우리는 '가격선'이라는 용어를 두 개의 무관심 곡선에 공통적으로 접하는 것을 나타내기 위해 사용할 것이다. 따라서 균형은 또한 가격선인 예산선과 일치하며, equlibrium에서의 가격은 선의 기울기이다. 그림 3 Ω은 기부금이고 Ω'은 평형 할당이다.

이에 대한 이면의 추리는 다음과 같다.

첫째로, 상자 안의 어떤 지점도 정확히 애비의 무관심 곡선 중 하나와 옥타비오 곡선 중 하나에 놓여 있어야 한다. 곡선이 교차할 경우(그림 4 참조) 바로 이웃을 네 개의 영역으로 나누고, 그 중 하나는 (연녹색으로 표시) 양쪽 소비자에게 선호된다. 따라서 무관심 곡선이 교차하는 지점은 equlibrium이 될 수 없으며, 평형은 접선점이어야 한다.

둘째로, 접선 시점의 시장에서 보유할 수 있는 유일한 가격은 접선 경사가 주는 가격이다. 왜냐하면 이 가격에서만 소비자들은 제한적으로 작은 교환을 기꺼이 받아들이기 때문이다.

그리고 세 번째(가장 어려운 점) Ω에서 평형까지의 경로로 소비자를 데려가는 모든 교환은 동일한 가격으로 이루어져야 한다. 만약 이것이 받아들여진다면, 그 가격은 접선점에 있는 하나의 운영자여야 하며, 그 결과는 다음과 같다.

2인 경제에서는 모든 교류가 같은 가격으로 이루어진다는 보장이 없다. 그러나 엣지워스 박스의 목적은 경쟁이 없을 때 일어날 수 있는 가격 담합을 설명하기 위한 것이 아니라, 최소한의 경우에 경쟁력 있는 경제를 설명하기 위한 것이다. 그래서 우리는 하나의 Abby와 하나의 옥타비오 대신에 각각의 복제품들을 무한히 많이 가지고 있으며, 서로 다른 시기에 동일한 기부금을 가지고 시장에 나와 점차 평형을 이루도록 협상하고 있다고 생각할 수 있다. 새로 도착한 옥타비오는 평형에 가까운 애비와 시장가격으로 교환할 수 있으며, 새로 도착한 애비가 거의 만족한 옥타비오와 교환하는 한 그 숫자는 균형을 이룰 것이다. 큰 경쟁 경제에서 교환이 통하려면 모두에게 같은 대가가 지배해야 한다. 그러므로 교환은 우리가 정의한 대로 가격선을 따라 할당을 이동시켜야 한다.^[12]

그에 따라 경쟁적 평형을 찾는 과제는 접선이 주어진 지점을 통과하는 두 개의 무관심 곡선 사이의 접점을 찾는 작업으로 줄어든다. 오퍼 곡선(아래 설명)을 사용하면 이를 위한 체계적인 절차가 제공된다.

파레토 세트

상품 배분은 한 소비자에게 더 유리하고 다른 소비자에게 더 나쁠 것이 없다면 다른 소비자에게 '파레토'를 지배하는 것이라고 한다. 할당량은 다른 할당인 파레토가 지배하지 않으면 '파레토 최적'(또는 '파레토 효율')이라고 한다. 파레토 최적 할당 세트는 파레토 세트(또는 '효율적인 위치')로 알려져 있다.

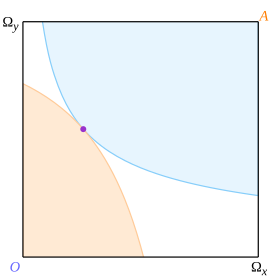
보라색 점으로 접선점을 표시하는 그림 5에서와 같이 각 소모 장치에 하나씩 접선 곡선 한 쌍을 고려하십시오. 그러면 볼록성은 곡선이 접선점 이외에는 가로챌 수 없다는 것을 보장하고, 이에 따라 박스는 3개의 영역으로 나뉜다. 엷은 푸른색 영역은 옥타비오보다 접선 지점이 더 좋지만 애비에게는 더 나쁘다; 엷은 주황색 영역은 애비에게는 더 좋지만 옥타비오에게는 더 나쁘다; 그리고 흰색 영역은 둘 다 더 나쁘다. 유사한 고려사항이 경계에도 적용된다. 접선 지점은 파레토 최적점이라는 것이 뒤따른다.

따라서 파레토 집합은 곡선의 접선점에 대한 위치다. 옥타비오의 출신(O)과 애비의 출신(A)을 잇는 선이다. 예를 들면, 보라색 선이 두 소비자의 무관심 곡선에 해당하는 파레토 세트인 그림 6에 나타나 있다.

엣지워스 박스의 일부인 다른 사물을 설명하는 데 사용되는 어휘는 다양하다. 파레토 세트 전체를 계약 곡선이라고 부르기도 하는 반면, 마스 콜렐 외는 계약 곡선의 정의를 적어도 애비와 옥타비오 둘 다 초기 기부금만큼 부유하게 만드는 파레토 세트의 포인트로만 제한한다. 마틴 오스본, 아리엘 루빈스타인 등 게임 이론적으로 좀 더 구부러진 다른 작가들은 적어도 초기 기부금만큼 각 소비자에게 좋은 파레토 세트 부분에 코어라는 용어를 사용한다.^[13]

파레토 세트는 소비자의 무관심 곡선이 접선하는 포인트 세트인 만큼 각 소비자의 한계 대체율이 상대방과 동일한 포인트 세트이기도 하다.^[14]

복지경제학의 제1차 기본정리

우리는 무관심 곡선의 접점들이 파레토 옵티마라고 보아왔지만, 우리는 또한 이전에 경제적 평형성이 무관심 곡선이 공통의 가격선에 접하는 지점이라는 것을 보았다. 그것은 평형제가 정확히 파레토 옵티마라는 것을 따른다.

This argument applies with one restriction even if the curves are undifferentiable or if the equilibrium is on the boundary. The condition for equilibrium is that no further exchange will take place, and the condition for no further exchange to take place is that there is no direction of motion which benefits one consumer without harming the other; and this is equivalent to the definition of a Pareto optimum.^[15]

The restriction is that equilibrium implies that no local improvement can be made – in other words, that the point is 'locally' Pareto optimal. But Pareto optimality is nowadays considered global by definition.^[16] Thus if the nature of the indifference curves allows non-global optima to arise (as cannot happen if they are convex), then it is possible for equilibria not to be Pareto optimal.

Perfect competition is not a precondition for the theorem. So long as the consumers are free to exchange, and will continue to do so until no mutually acceptable exchange is available, equilibrium will be reached and will be (at least 'locally') Pareto optimal.^[17]

The second fundamental theorem of welfare economics

Now consider an economy in which the consumers have endowments ω as shown in Fig. 7. Left to itself a free market will take them to ω'. But suppose that some other position in the box – say α' – is considered socially preferable. We can assume that the socially desired position is Pareto optimal.

We may think of the price lines (shown as dashed in the diagram) as corresponding to different distributions of real income, and movement along them as reallocation of resources while incomes remain fixed.

Then in order to reposition society at the desired point α' it is not necessary for the government to redistribute resources in such a way that Octavio holds (α'_x,α'_y) and Abby holds the complement: it is sufficient to reallocate resources to take the economy to any point (say α) on the price line through α', and then leave the market to find its own equilibrium. Indeed, so long as the government recognises a desirable distribution of income it does not need to have any idea of the optimal allocation of resources.

좀 더 일반적인 경제를 위한 성명에서, 그 정리는 α'가 통화 이전을 거쳐 시장 교환의 자유로운 플레이에 의해 도달할 수 있다고 말하지만, 엣지워스 박스에는 돈이 없다.

두 번째 근본적인 정리는 사회의 병폐를 바로잡는 청사진을 제시하지 못한다. 정부는 옥타비오와 애비 사이에 자원을 재할당하기로 결정하여 당일 거래에 앞서 Ω에서 α로 이동할 수 있으며, 결과적으로 손해를 보는 사람은 다음 날 시장에 덜 가져가기로 결정할 수도 있다. 두 번째 기본 정리는 재분배에 의해 도입된 왜곡을 고려하지 않는다.^[18]

제안 곡선

오퍼 곡선은 평형점을 찾는 수단을 제공하며, 또한 그들의 존재와 독특성을 조사하는 데도 유용하다.

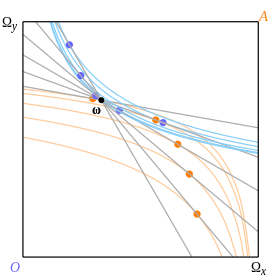
각 소비자와 기부금에 따라 두 가지 곡선 모두 상자에 그릴 수 있다. 우리는 약 Ω의 예산 라인을 회전시키고 그림 8의 색 점으로 나타낸 것과 같이 두 소비자가 가장 선호하는 포인트를 따라 추적한다. 이것들은 선이 그들 자신의 무관심 곡선에 접하는 지점이다.

소비자가 가장 선호하는 포인트의 중심은 제안곡선이다. 그림 9는 옥타비오의 제안곡선을 짙은 청색으로, 애비는 갈색처럼 보인다. 그들은 Ω' 지점에서 만나고 평형예산선(회색으로 그려짐)은 이 지점을 통과하는 선이다. 두 소비자에 대한 무관심 곡선은 더 선명한 색상으로 나타난다.

오퍼 곡선은 반드시 기부 포인트 Ω을 통과한다. 우리가 Abby를 예로 든다면, 그녀의 무관심 곡선 중 하나는 Ω을 통과해야 하며, 예산 라인은 이곳의 무관심 곡선과 동일한 구배를 갖도록 선택될 수 있어 Ω이 이 라인에 가장 선호하는 포인트가 될 수 있다는 것을 우리는 주목한다.

결과적으로 두 소비자의 제안 곡선은 반드시 Ω으로 교차하지만, 이를 가능하게 하는 특성은 Ω이 다른 경사의 예산 라인과 일치하는 유일한 교차점이며, 따라서 반드시 평형을 구성하지는 않는다는 것이다.

Ω이 아닌 지점에서 제안 곡선의 교차점은 안정적인 평형을 결정한다. 만약 두 제안 곡선이 기부 포인트에서 접선된다면, 이 포인트는 정말로 평형이고 그들의 공통 접선은 해당 예산 라인이다.^[19]

제안 곡선에 대한 용어

제안 곡선은 Vilfredo Pareto에 의해 처음 사용되었다 – 그의 Manuale/Manuel Chap을 참조하라. §97. III 그는 그들을 '교환 곡선'(linee dei baratti/lignes des échanges)이라고 불렀고, 옥타비오가 예산 라인을 따라 선호하는 할당에 대한 그의 이름은 그의 '균형점'이었다.

오늘날 선호되는 이러한 할당을 옥타비오의 '수요'라고 부르기도 하는데, 이는 대칭적 사실에 대한 비대칭적인 설명을 구성한다. 할당량은 애비의 옥타비오만큼의 보유량을 결정하며, 따라서 수요만큼의 공급량이다.

오프레는 프랑스어로 '공급'을 의미하기 때문에, 제안곡선을 수요의 중심이라고 부르는 것은 공급곡선을 수요의 중심이라고 부르는 것과 같다.

평형주의 고유성

주어진 기부를 통해 공유 접선이 존재하며, 무관심 곡선이 그 형태에 병적인 것이 아니라면 접선의 지점이 독특할 것이라는 것은 경제적인 고려에서 추측할 수 있을 것이다. 이것은 사실이 아닌 것으로 밝혀졌다. 평형의 고유성에 대한 조건은 광범위한 연구의 주제였다: 일반 평형 이론을 참조하라.

그림 9와 10은 3개의 뚜렷한 평형률이 기부 포인트 Ω에 해당하는 Mas-Colell 외 연구소의 예를 예시한다. 무관심 곡선은 다음과 같다.

${\displaystyle x}$- ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle {\mathrm{8y}}^{}}$- 8${\displaystyle {}^{}}$= ${\displaystyle u}$ ${\displaystyle \quad x-{\tfrac {1}{8}y^{-8}=u}($Octavio)

${\displaystyle y}$- 1 ${\displaystyle 8\frac{\mathrm{}}{}}$ ${\displaystyle x{}^{}}$- ${\displaystyle 8^{}}$= ${\displaystyle u}$ ${\displaystyle \quad y-{\tfrac {1}{8}x^{-8}=u}($Abby)

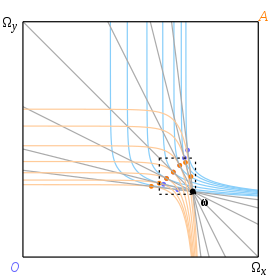
무관심 곡선은 상자를 가득 채우지만 일부 대표적인 예산 라인과 접해 있을 때만 나타난다. 그림 11에 그려진 오퍼 곡선은 큰 회색 점으로 표시된 세 지점에서 교차하며, 이 값은 다음과 같다. 1⁄2, 1과 2

일반화

평형의 성질에 대한 초기 검사는 접선이라는 암묵적 정의에 기초했으며, 볼록성은 암묵적으로 가정된 것으로 보인다.^[20] 평형에 도달할 것이라는 것에는 의심의 여지가 없었다: 경사도가 상승하면 평형이 될 것이다. 그러나 결과는 일반성이 결여되어 있었다.

경계 평형 및 비차별 곡선

케네스 애로우와 제라드 데브루는 1951년에 독립적으로 논문을 발표하여 평형 이론의 미적분학적 증명에서의 한계에 주목하였다.^[21] 화살은 특히 경계의 평형성에 의해 야기되는 어려움과 데브레우에게 차별화되지 않는 무관심 곡선의 문제를 구체적으로 언급했다.

철저한 커버리지를 목표로 하지 않는다면, 이러한 경우에 적용하기 위해 우리의 방법을 어떻게 확장하는지를 직관적으로 쉽게 알 수 있다. 우리는 곡선에 닿는 어떤 선, 즉 미분적분보다 어원적 의미의 탄젠트를 포함하도록 탄젠트의 개념을 넓힐 필요가 있다. 그림 12의 예에서, 접촉점을 통한 법적 가격선이 있으며, 각 호는 박스 내부에 절단하지 않고 무관심 곡선을 만지고, 따라서 주어진 기부금에 대한 가능한 평형 범위가 있다.

경쟁균형

그림 12의 평형도는 곡선이 서로 진정한 접선인 점이 아니다. 그러나 접선의 관점에서 정의를 일반화하는 특성을 가지고 있는데, 이는 두 곡선이 직선으로 국소적으로 분리될 수 있다는 것이다.

Arrow와 Debreu는 1951년의 (독립) 논문에서 평형을 서로와 같은 방식으로 정의했으며, 그 정의에 대한 어떠한 출처나 근거도 제공하지 않았다. 그들은 1954년의 공동 논문(균형 존재에 관한)^[22] 새로운 정의는 미분학에서 볼록 집합 이론으로 수학적 기법을 변경해야 했다.

그들의 실제 정의는 다음과 같다: Ω에서 얻을 수 있는 평형은 x와 Ω을 통한 할당 x와 예산 라인으로 구성된다. 따라서 소비자 중 어느 한쪽이 x를 선호하는 라인에 따라 포인트가 없다. 할당과 이 속성을 만족시키는 라인으로 구성된 한 쌍을 '월라시안' 또는 '경쟁력'이라고 한다. 평형을 유지하다

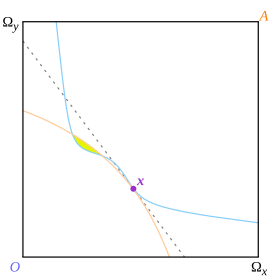
이 정의의 예산선은 두 소비자의 무관심 곡선을 가르는 선이지만, 지역적이기보다는 세계적으로 그러하다. 애로우와 데브루는 왜 글로벌 분리가 필요한지에 대해서는 설명하지 않고 있는데, 이는 그들의 증거를 쉽게 만들었을지 모르지만 예상치 못한 결과를 초래할 수 있다. 그림 13에서 포인트 x는 접선점이며, 또한 무관심 곡선이 파선 가격선에 의해 국지적으로 분리되는 지점이기도 하지만, 전체적으로 분리되지 않기 때문에 포인트는 Arrow와 Debreu의 정의에 따라 평형이 아니다.

그림 14에서 포인트 x는 경쟁 평형의 정의를 충족하지 않는 파레토 최적점이다. 경제가 그러한 시점에 안착할 것인가에 대한 문제는 그것이 평형의 일정한 정의를 충족시킬 것인가 하는 것과 상당히 별개의 것이다; 분명히 이 경우에는 정말로 거기에 안착할 것이다.

Arrow와 Debreu는 그들의 '추측' 사이에 항상 무관심 곡선의 대류를 포함했다. '가정'이라는 용어는 모호한 것으로서, 이론뿐만 아니라 기본적인 정의들을 전제로 하거나, 또는 후자에게만 필요한 전제를 언급할 수 있다. 이들의 정의가 곡선이 비콘벡스일 때 존재할 수 있는 모든 평형을 포함하고 있지 않기 때문에, 이전의 의미에서는 볼록성의 가정을 의미했을 가능성이 있다. 이것이 그렇든 아니든, 그 정의는 도메인의 제약 없이 널리 채택되어 왔다.

때로는 그 정의에 따라 결과가 도출될 수 있다는 것이 증명(복지경제학의 첫 번째 근본적인 정리가 본보기가 되는 것)에 있어서 볼록함을 가정하지 않고도 밝혀져 왔다.

경쟁균형유존재

일부 경제에서는 균일한 가격으로 교환함으로써 주어진 기부금에서 도달할 수 있는 휴식처가 없을 것이다. 따라서 경쟁적 균형에 대한 정의를 충족하는 휴식처는 존재하지 않는다. 그림 14의 패턴 곡선 계열이 이에 대한 예다.

복지경제학의 기본이론

'경쟁 평형'으로 정의된 평형 상태에서 무관심 곡선이 볼록할 필요가 없더라도 첫 번째 기본 정리를 증명할 수 있다: 어떤 경쟁 평형도 (광택적으로) 파레토 최적이다. 그러나 그 증거는 더 이상 명백하지 않고, 독자는 복지경제학의 기본 이론에 관한 기사를 참조한다.

평형의 접선적 정의에 따라 동일한 결과가 (비콘벡스 무관심 곡선으로) 유지되는 것으로 간주되지 않았을 것이다. 그림 13의 점 x는 노란색의 파레토가 지배하기 때문에 (광택적으로) 최적 상태가 아닌 평형으로 간주되었을 것이다.

평형 달성이 의심스러워진 만큼 결과가 강화되지 않은 것은 아니다. 그림 13에서 포인트 x는 '경쟁력 평형'이 아닐 수 있지만, 경제는 황색 지역에서 '진정한'(그리고 파레토 최적) 평형에 도달하는 것을 막으면서 거기에 고착될 수 있다.

평형이 실제로 달성될 것이라는 것은 언제나 최초의 복지 정리에 필수적인 것으로 여겨졌다. 레너의 정리 해석은 "다행히 최적의 상품배분이 자동으로 이루어질 수 있다"^[23]는 것이었다. 그러나 지역 최적화가 존재할 때 글로벌 최적화가 달성된다는 것을 보장할 수 있는 것은 아무것도 없다. 평형 개념이 x와 같은 국부적 최적점을 포함하는 경우 평형은 달성 가능하지만 차최적일 수 있다. 그러한 점이 제외되는 경우 평형은 최적일 수 있지만 달성 불가능할 수 있다.

비합법성에 의한 차이는 제2차 기본 정리를 보면 더욱 뿌리 깊게 된다. 모든 파레토 최적화가 경쟁적 균형인 것은 아니다(여전히 경제의 휴식처일 수도 있지만). 결과적으로 정리는 전제로서 선호의 대류성을 부여하거나, 아니면 위에서 정의한 대로 '균형'을 '경쟁적 평형'으로 이해되지 않는 방식으로 명기할 필요가 있다.

Notes

References

• Mas-Colell, Andreu; Whinston, Michael D.; Jerry R. Green (1995). Microeconomic Theory. New York: Oxford University Press. ISBN 0-19-507340-1.
• Vilfredo Pareto, Manuale di Economia Politica con una Introduzione alla Scienza Sociale (1906) / Manuel d'Économie Politique (1909) (effectively a second edition of the Italian version), Eng. tr. (of the French) as "Manual of Political Economy" (1971). The Italian text is available online at https://archive.org/details/manualedieconomi00pareuoft.

외부 링크

• 시뮬레이션(Wolfram.com)
• 경제 진실에 대한 에지워스 박스 설명
• 디지털 이코노미스트의 엣지워스 박스 설명