동적 모드 분해

이 글에는 여러 가지 문제가 있다.이 문제를 개선하거나 대화 페이지에서 토의하십시오.(이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글에는 아마도 독창적인 연구가 포함되어 있을 것이다. 클레임을 확인하고 인라인 인용문을 추가하여 개선하십시오. 원본 연구로만 구성된 문장은 제거해야 한다.(2012년 3월) (이 템플릿 메시지를 제거하는 방법과 시기 학습) 이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "동적 모드 분해" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2012년 3월) (이 템플릿 메시지를 제거하는 방법과 시기 학습) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

동적 모드 분해(DMD)는 2008년 피터 슈미드가 개발한 차원성 감소 알고리즘이다.일련의 데이터를 고려하여 DMD는 고정 진동수 및 붕괴/성장률과 관련된 일련의 모드를 계산한다.특히 선형 시스템의 경우 이러한 모드와 주파수는 시스템의 정상 모드와 유사하지만, 보다 일반적으로 구성 연산자(Kopman 연산자라고도 함)의 모드와 고유값의 근사치들이다.DMD는 각 모드와 관련된 고유 시간적 동작 때문에 미리 정해진 시간적 동작이 부족한 직교 모드를 계산하는 주성분 분석과 같은 차원성 감소 방법과 다르다.그것의 모드는 직교하지 않기 때문에, DMD 기반 표현은 PCA에 의해 생성된 표현보다 덜 파시모닉할 수 있다.그러나 각 모드는 적시에 축축한(또는 구동된) 사인파 동작과 연관되기 때문에 더 물리적으로 의미가 있을 수 있다.

개요

동적 모드 분해는 흐름 데이터에서 동적 특성을 추출하기 위한 수치적 절차로 Schmid에 의해 처음 도입되었다.^[1]

데이터는 스냅샷 시퀀스의 형태를 취함

${\displaystyle V_{1}^{N}=\{v_{1},v_{2},\dots,v_{N}\}}$

where ${\displaystyle v_{i}\in \mathbb {R} ^{M}}$ is the ${\displaystyle i}$-th snapshot of the flow field, and ${\displaystyle V_{1}^{N}\in \mathbb {R} ^{M\times N}}$ is a data matrix whose columns are the individual snapshots.이러한 스냅샷은 선형 동적 시스템을 정의하는 선형 매핑을 통해 관련되는 것으로 가정한다.

${\displaystyle v_{i+1}=Av_{i}}$

표본 추출 기간 동안 거의 동일하게 유지된다.매트릭스 형식으로 작성되었으며, 이는 다음을 함축한다.

${\displaystyle V_{2}^{N}=AV_{1}^{N-1}+re_{N-1}^{T}}}$

where ${\displaystyle r}$ is the vector of residuals that accounts for behaviors that cannot be described completely by ${\displaystyle A}$, ${\displaystyle e_{N-1}=\{0,0,\ldots ,1\}\in \mathbb {R} ^{N-1}}$, ${\displa$$ystyle V_{1}^{N-1}=\{v_{1},v_{2},\dots ,v_{N-1}\}}$, and ${\displaystyle V_{2}^{N}=\{v_{2},v_{3},\dots ,v_{N}\}}$. Regardless of the approach, the output of DMD is the eigenvalues and eigenvectors of ${\displaystyle A}$, which are referred to as the DMD eigenvalues and DMD modes resp…을 속여서

알고리즘.

이러한 고유값과 모드를 얻는 방법에는 두 가지가 있다.첫째는 아놀디 같은 것으로, 크릴로프 방법과의 연관성이 있어 이론 분석에 유용하다.두 번째는 데이터의 잡음과 수치 오류에 보다 강력한 SVD 기반 접근법이다.

아놀디 접근법

유체 애플리케이션에서, $스냅샷$의 크기인$$M {\$displaystyle M}$은(는$)$ N$${\$displaystyle$N$\}$보다 훨씬 큰 것으로 $가정$되므로$,$ A {\$displaystyle A}$의 유효 선택 항목이 많이 있다$.$원래 DMD 알고리즘은 $V{\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$의 각 스냅샷을 $V{\displaystyle {}_{}^{}}$ 1 ${\displaystyle {N\mathrm{}}_{}^{}}$- ${\displaystyle 1_{}^{}}$ ${\$의 스냅샷의 선형 조합으로 표현할 수 있도록$$$$ A ${\displaystystyle A}$를 선택한다$.$ 두 데이터 집합에 대부분의 스냅샷이 나타나기 때문에 이 표현은 무료 오류다.ll 스냅샷(${\displaystyle v_{}}$ N ${\$ 제외$)$으로 기록됨

${\displaystyle v_{N}=a_{1}v_{1}v_{1}+a_{2}v_{2}+\dots +a_{N-1}+{N-1}+r=V_{1}^{N-1}a+r,},}$

여기서 $a{\displaystyle }$= ${\displaystyle {a\mathrm{}}_{}}$ ${\displaystyle 1{}_{}}$,${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle {}_{}}$- ${\displaystyle 1_{}}$ ${\$는 DMD가 식별해야 하는 계수 집합이고$$ r ${\displaysty$ r$}$은 $잔차$임.다 합쳐서.

${\displaystyle V_{2}^{N}=AV_{1}^{N-1}+re_{N-1}^{{N-1}^{N-1}}}T}=V_{1}^{N-1}S+re_{N-1}^{T}}}$

여기서 $S{\displaystyle }$ ${\displaystyle S}$은(는) 동반 매트릭스임

${\displaystyle S={\begin{pmatrix}0&0&\dots &0&a_{1}\\1&0&\dots &0&a_{2}\\0&1&\dots &0&a_{3}\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\dots &1&a_{N-1}\end{pmatrix}}.}$

벡터 $a{\displaystyle }$ ${\displaystyle a}$는 전체 잔차를 최소화하는 최소 제곱 문제를 해결하여 계산할$$ 수 있다.특히 $V{\displaystyle {}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{N}}_{}^{}}$- ${\displaystyle {}_{}^{}}$= ${\displaystyle Q}$ ${\displaystyle R}$ ${\displaystyle V_{1}^{N-1}=$QR$\}$의 QR 분해를 취하면 $a{\displaystyle }$= ${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\displaystyle {}^{}{}^{}}$ ${\displaystyle {}^{}{}_{}}$ N ${\$$T}v_{N}}$.

In this form, DMD is a type of Arnoldi method, and therefore the eigenvalues of ${\displaystyle S}$ are approximations of the eigenvalues of ${\displaystyle A}$. Furthermore, if ${\displaystyle y}$ is an eigenvector of ${\displaystyle S}$, then ${\displaystyle V_{1}^{N-1}y}$ is an approximate$A{\displaystyle }$ ${\displaystyle A}$의 고유 벡터$.$$A{\displaystyle }$ {\$displaystyle A}$이 아닌 S ${\$ S$}$에서 eigende composition을 수행하는 이유는 S ${\displaystyle S$$}$이(가) $A{\displaystyle }$ ${\$displaysty A}보다 훨씬 작기 때문에 DMD의 계산 비용은 스냅샷 크기가 아니라 스냅샷 수에 의해 결정되기 때문이다$.$

SVD 기반 접근 방식

동반 행렬 S ${\displaystyle$ S$}$을(를) 계산하는 대신$,$ SVD 기반 접근방식은 유사 변환을 통해$$ $A{\displaystyle }$ ${\displaystyle A}$과$($와) 관련된$$ 행렬${\displaystyle \stackrel{}{}}S{\displaystyle \stackrel{}{}}$ ~ {\displaystyle {S}을$($를) 산출한다.이를 위해 $V{\displaystyle {}_{}^{}}$ 1 ${\displaystyle {\mathrm{N}}_{}^{}}$- 1${\displaystyle {}_{}^{}}$= ${\displaystyle U}$ ${\displaystyle \mathrm{\sigma }}$ ${\displaystyle W^{}}$ T ${\$의 SVD가 있다고 가정해 보십시오$.$ 그렇다면

${\displaystyle V_{2}^{N}=AV_{1}^{N-1}+re_{N-1}^{{N-1}^{N-1}}}T}=AU\Sigma W^{T}+re_{N-1}^{T}.}$

아놀디 기반 접근법에 의한 가정과 동등하게, $우리$는 V ${\displaystyle {}_{}^{}}$ ${\$의 $스냅샷$이 U ${\displaystyle U}$의 열의 선형 중첩으로 기록될 수 있도록$$$$ $A{\displaystyle }$ ${\displaystyle A}$을(를) 선택하며$,$ 이는 해당 열을 PO의 중첩으로 작성할 수 있도록 요구하는 것과 동일하다.D 모드.이 제한에서 잔차를 최소화하려면 POD 기준과 직교해야 한다($즉{\displaystyle {}^{}}$, U T ${\displaystyle {}^{}}$= ${\displaystyle 0}$ ${\displaystyle$ U$^{$$T}r=0}$ $$.그런 다음 위의 방정식의 양쪽에 ${\displaystyle U^{}}$ T ${\$$T}$ 산출$$ $U{\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\displaystyle {}^{}{}_{}^{}}$ ${\displaystyle {}_{}^{}}$= ${\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle U}$ U U U ${\displaystyle w^{}}$ W$T$ {\$displaystyle U^{T}V_{2}^{$N}=$U^{{}}$$조작하여 얻을$ 수 있는 T}$AU\Sigma$ W$^{T$

$U^{T}AU=U^{T}V_{2}^{N}W\Sigma ^{-1}\equiv {\tilde {S}}.}$

Because ${\displaystyle A}$ and ${\displaystyle {\tilde {S}}}$ are related via similarity transform, the eigenvalues of ${\displaystyle S}$ are the eigenvalues of ${\displaystyle A}$, and if ${\displaystyle y}$ is an eigenvector of ${\displaystyle {\tilde {S}}}$, then ${\displ$$aystyle Uy}$은(는) $A{\displaystyle }$ ${\displaystyle A}$의 고유 벡터다$.$

요약하면 SVD 기반 접근법은 다음과 같다.

1. V ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$의 데이터 시계열을 두 행렬 $V{\displaystyle {}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$ N${\displaystyle {}_{}^{}}$- ${\displaystyle 1_{}^{}}$ ${\$ 및$$ V ${\displaystyle {}_{}^{}}$ ${\$로 분할하십시오$.$
2. $V{\displaystyle {}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$- ${\displaystyle 1_{}^{}}$= ${\displaystyle U}$ ${\displaystyle \mathrm{\sigma }}$ ${\displaystyle W^{}}$ T ${\$ W$^{T}$의 SVD를 계산한다$.$
3. $Matrix{\displaystyle \stackrel{}{}}$ S${\displaystyle \stackrel{}{~}}$= ${\displaystyle {}^{}}$ T ${\displaystyle {}^{}{}_{}^{}}$ 2 ${\displaystyle {N\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle 1^{}}$ ${\displaystyle {-}^{}}$ 1 ${\$$T}V_{2}^{N$}^{N$}W\Sigma ^{-1$ 고유값 ${\displaystyle {\lambda }_{}}$ i ${\$ 및$$ 고유 $벡터{\displaystyle {}_{}}$ y ${\displaystyle i_{}}$ ${\$을(를) 계산한다$.$
4. $i{\displaystyle }$ ${\displaystyle$ i$}$ -th$$ DMD 고유값은 ${\displaystyle {\lambda }_{}}$ i ${\$이고, $i{\displaystyle }$ ${\displaysty i}$ -th$$ DMD 모드는 $U{\displaystyle }$ ${\displaystyle y_{}}$ i ${\$이다$.$

으로서[1]에 정확하게 첫번째 커플 모드와 eigenvalues보다 더 많은 컴퓨팅 실험에 어려울 수 있다는 점에 주목하는SVD-based 접근법의Arnoldi-like 접근에 대한 장점은 데이터 및 숫자 절단 문제에 소음을 − 1{\displaystyle V_{1}^{N-1}}은 simultaneousV1N의 버림으로써 보상 받을 수 있습니다.da이 잘림 단계가 없는 ta 세트.

이론적 및 알고리즘적 진보

2010년 처음 시작된 이래, 상당한 양의 작업이 DMD 이해와 개선에 집중되었다. Rowley ^[2]외 연구원의 DMD에 대한 첫 번째 분석 중 하나는 DMD와 Koopman 운영자 간의 연결을 확립하고 비선형 시스템에 적용할 때 DMD의 출력을 설명하는 데 도움을 주었다.그 이후로, 이 연결을 더욱 강화하거나 접근방식의 견고성과 적용가능성을 향상시키는 많은 수정이 개발되었다.

• 최적화 DMD: 최적화 DMD는 (i) DMD 모드 선택 난이도와 (ii) 시계열의 마지막 스냅샷에서 소음이나 기타 오류에 대한 DMD의 민감도라는 두 가지 접근법의 한계를 보완하도록 설계된 원래의 DMD 알고리즘의 수정이다.^[3]최적화된 DMD는 식별된 선형 연산자가 고정된 순위를 갖는 최적화 문제로 DMD 절차를 다시 시작한다.더욱이, 마지막 스냅샷을 제외한 모든 스냅샷을 완벽하게 재현하는 DMD와 달리, Optimized DMD는 재구성 오류를 데이터 세트 전체에 분산시킬 수 있게 해, 실제로 접근법을 더욱 견고하게 만드는 것으로 보인다.
• 최적 모드 분해:최적 모드 분해(OMD)는 DMD 절차를 최적화 문제로 다시 시작하고 사용자가 식별된 시스템의 순위를 직접 부과할 수 있도록 한다.^[4]이 순위를 적절하게 선택할 경우, OMD는 합성 및 실험 데이터 세트 모두에서 잔차 오차가 작고 보다 정확한 고유값을 갖는 선형 모델을 생성할 수 있다.
• 정확한 DMD: 정확한 DMD 알고리즘은 두 가지 방법으로 원래의 DMD 알고리즘을 일반화한다.먼저 원래 DMD 알고리즘에서 데이터는 스냅샷의 시계열이어야 하지만 정확한 DMD는 스냅샷 쌍의 데이터 세트를 허용한다.^[5]쌍의 스냅샷은 고정 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle t}$ ${\displaystyle \Delta t$ 로 분리해야 하지만 단일 시계열에서 그릴 필요는 없다.특히 정확한 DMD는 여러 실험에서 얻은 데이터를 하나의 데이터 세트로 통합할 수 있다.둘째, 원래의 DMD 알고리즘은 일련의 POD 모드에 투영함으로써 데이터를 효과적으로 사전 처리한다.정확한 DMD 알고리즘은 이 전처리 단계를 제거하고 POD 모드의 중첩으로 쓸 수 없는 DMD 모드를 만들 수 있다.
• Sparsity Promotion DMD: Sparsity 프로모션 DMD는 DMD 모드와 고유값 선택을 위한 사후 처리 절차다.^[6]DMD를 촉진하는 스파시티는 ${\displaystyle {important\mathrm{}}_{}}$ 1 ${\$벌칙을 사용하여 중요한 DMD 모드의 작은 세트를 식별하며, 볼록 최적화 기법을 사용하여 효율적으로 해결할 수 있는 DMD 모드 선택 문제에 대한 대안적 접근법이다.
• 다중 분해능 DMD: 다중 분해능 DMD(Multi-Defolution DMD)는 다중 분해능 분석에 사용되는 기법과 다중 시간 분산을 포함하는 데이터 세트의 고유값과 DMD 모드를 강력하게 추출하도록 설계된 정확한 DMD를 결합한 것이다.^[7]MRDMD 접근방식은 지구 표면 온도 데이터에 적용되었고, 엘니뇨 기간 동안 나타나는 DMD 모드를 식별한다.
• 확장 DMD: 확장 DMD는 DMD와 Kopman 운영자 사이의 연결을 강화하는 정확한 DMD의 수정이다.^[8]이름에서 알 수 있듯이, Extended DMD는 더 풍부한 관측 가능한 기능 집합을 사용하여 Koopman 운영자의 보다 정확한 근사치를 산출하는 DMD의 확장이다.또한 DMD와 관련 방법은 더 일반적으로 사용되는 고유값과 모드 외에 Koppman 고유특성의 근사치를 산출한다는 것을 입증하였다.
• DMD(제어 포함):제어(DMDc)를 이용한 동적 모드 분해는 입력 출력 시스템에서 얻은 데이터를 위해 설계된 DMD 절차의 수정이다.DMDc의 한 가지 독특한 특징은 시스템 작동의 영향을 개방 루프 역학으로부터 분리하는 능력인데, 작동 상태에서 데이터를 얻을 때 유용하다.
• Total Last Square DMD: Total Last Square DMD는 데이터의 측정 노이즈에 대한 강건성 문제를 해결하기 위한 정확한 DMD의 최근 수정이다.저자들은 정확한 DMD를 일반 최소 제곱법(OLS)을 사용해 해결되는 회귀 문제로 해석하는데,^[10] 이는 퇴행기가 소음이 없는 것으로 가정한다.이 가정은 모든 관측치가 노이즈가 있는 실험 데이터 세트에 적용할 때 DMD 고유값에 치우침을 생성한다.총 최소 제곱 DMD는 OLS 문제를 총 최소 제곱 문제로 대체하며, 이는 이러한 편향을 제거한다.
• 동적 분포 분해: DDD는 연속 시간, 즉 전달 연산자의 전방 문제에 초점을 맞춘다.그러나 개발된 방법은 DMD 문제를 연속 시간에 맞추는 데도 사용할 수 있다.^[11]

여기에 열거된 알고리즘 외에도 유사한 애플리케이션별 기법이 개발되었다.예를 들어, DMD와 마찬가지로 프론의 방법은 감쇠된 사인파의 중첩으로서 신호를 나타낸다.기후과학에서는 선형 역방향 모델링도 DMD와 강하게 연결되어 있다.^[12] 보다 포괄적인 목록은 Tu et al을 참조한다.^[5]

예

이 절에는 아마도 독창적인 연구가 포함되어 있을 것이다. 클레임을 확인하고 인라인 인용문을 추가하여 개선하십시오. 원본 연구로만 구성된 문장은 제거해야 한다.(2012년 3월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

종단의 후행 에지

흐름에 장애물이 생기면 카르만 소용돌이 거리가 생길지도 모른다.그림 1은 종단의 후미진 가장자리 뒤쪽의 소용돌이의 탈출을 보여준다.DMD 분석은 90개 순차 엔트로피 필드(애니메이션 gif(1.9))에 적용했다.MB)) 및 아래 그림과 같이 근사치 고유값 스펙트럼을 산출한다.이 분석은 지배 방정식을 참조하지 않고 수치 결과에 적용되었다.그 프로필은 흰색으로 보인다.흰색 호는 서로 다른 계산 블록을 사용하여 병렬 컴퓨터에서 연산이 수행되었기 때문에 프로세서 경계선이다.

스펙트럼의 약 3분의 1이 고감쇠 상태였으며($대형{\displaystyle {}_{}}$, ${\displaystyle {음극}_{}}$ {$$r {\$displaystyle \lambda _{$r$\})$는 표시되지 않는다.우세한 드리핑 모드는 다음 그림에 나타나 있다.왼쪽의 이미지는 실제 부분, 오른쪽의 이미지, 고유벡터의 상상적인 부분이다.

다시, 엔트로피-유전자 벡터가 이 그림에 나타나 있다.동일한 모드의 음향 내용은 다음 플롯의 하단에 나타난다.상단 절반은 위와 같이 엔트로피 모드에 해당한다.

여행 패턴의 합성 예

The DMD analysis assumes a pattern of the form ${\displaystyle q(x_{1},x_{2},x_{3},\ldots )=e^{cx_{1}}{\hat {q}}(x_{2},x_{3},\ldots )}$ where ${\displaystyle x_{1}}$ is any of the independent variables of the problem, but has to be select미리미리 에이드예를 들어 패턴

${\displaystyle q(x,y,t)=e^{-i\omega t}{\hat {{q}(x,t)^{-(y/b)^{2}}\re \e^{i(kx-\omega t)}}\right\}+{\text{random noise}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}?$

미리 선택된 지수 인자로 시간.

Ω${\displaystyle }$= ${\displaystyle 2\mathrm{\Omega }}$ / 0.1 ${\displaystyle \omega =2\pi /0.$1$\},$ $b{\displaystyle }$= ${\displaystyle 0.02}$ ${\displaystyle b=0.02},$ $k$ = ${\displaystyle 2}$ ${\displaystyle \pi }$/ ${\displaystyle b}$ ${\displaystyle k=2\pi /b}$ 등의 그림에서 샘플이 제공된다. 왼쪽 그림에는 노이즈가 추가된 패턴이 있다$.$무작위 노이즈의 진폭은 패턴의 진폭과 동일하다.

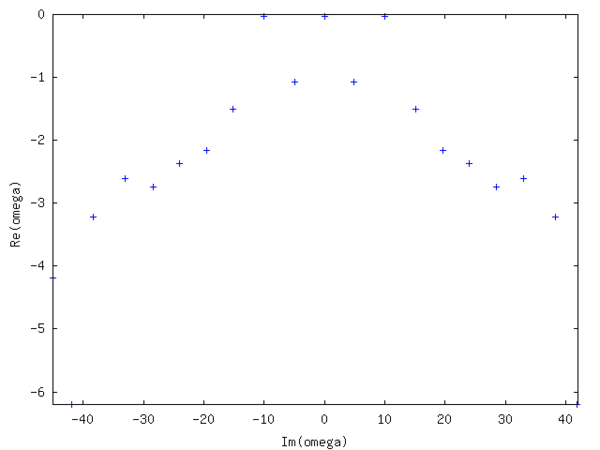
DMD 분석은 시간 간격 ${\displaystyle \Delta }$ t${\displaystyle }$= 1${\displaystyle }$/ ${\displaystyle \text{90}}$ s ${\$을 사용하여 21개의 합성 생성 필드를 사용하여 수행되며$,$ $분석$은${\displaystyle }$f = ${\displaystyle 45}$ ${\displaystyle \text{Hz}}${\$displaystyle f=45{\text}}$로 제한된다$.$

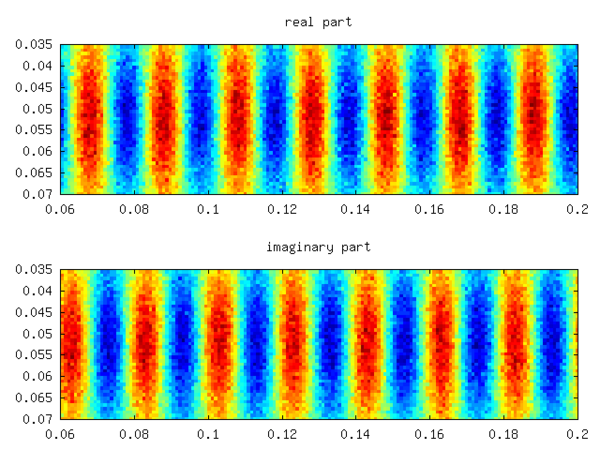
스펙트럼은 대칭이며 거의 감쇠되지 않은 모드(작은 음의 실제 부분) 3개를 보여주고, 다른 모드는 감쇠가 심하다.이들의 숫자 값은 각각$$ $\Omega {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$=${\displaystyle }$- ${\displaystyle 0.201}$ ,${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$/ ${\displaystyle {3\mathrm{}}_{}}$=${\displaystyle }$- ${\displaystyle 0.223}$± ${\displaystyle i}$ ${\displaystyle 62.768}$ ${\displaystyle \omega _{1}=-0.201,\omega _{2/3}=-0.223\pm i62.768}$이다.실제 오차는 필드의 평균에 해당하는 반면, ${\displaystyle {\Omega \mathrm{}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$/ 3 ${\$은${\displaystyle }$f = ${\displaystyle 10}$ ${\displaystyle \text{Hz}}${\$displaystyle f=10{\text{Hz}}}}$의 부과된 패턴에 해당한다$.$ 상대 오차는 -1/1000이다.노이즈를 신호 값의 10배까지 증가시키면 동일한 오류가 발생한다.후자의 두 가지 고유모드 중 하나의 실제와 상상의 부분이 다음 그림에 묘사되어 있다.

참고 항목

실험 데이터의 몇 가지 다른 분해들이 존재한다.지배 방정식을 사용할 수 있는 경우 고유값 분해가 가능할 수 있다.

• 고유값 분해
• 경험적 모드 분해
• 글로벌 모드
• 정상 모드
• 적절한 직교 분해
• 단수 값 분해

참조

• Schmid, P. J. & Sesthenn, J. L. 2008 수치 및 실험 데이터의 동적 모드 분해.인불.아머, 물리.Soc, 61번째 APS 회의, 페이지 208.샌안토니오.
• 하셀만, K, 1988년POP와 PIP.주 진동과 상호작용 패턴을 이용한 복합 동력학적 시스템의 감소.지오피스Res, 93(D9): 10975–10988.