드래그 곡선

Drag curve

항력 곡선 또는 항력 극성은 항공기의 항력과 리프트, 리프트 계수, 공격 각도 또는 속도와 같은 다른 변수 사이의 관계이다.이는 방정식으로 설명하거나 그래프(때로는 "극성 [1]그림"이라고도 함)로 표시할 수 있습니다.드래그(drag)는 실제 드래그 또는 드래그 계수로 표현될 수 있습니다.

드래그 곡선은 필요한 전력/속도 곡선 또는 싱크 속도/속도 곡선 등 드래그를 나타내지 않는 다른 곡선과 밀접하게 관련되어 있습니다.

드래그 곡선

NACA 636183 에어포일의 계수를 드래그 앤 리프트합니다.전체 곡선은 리프트, 점선 드래그이며, 빨간색 곡선은 R = 3/106, 파란색 9/10이다e6.
공격 각도에 대한 상승 및 항력 계수.
유도 항력, 기생 항력 및 총 항력을 공기 속도의 함수로 나타내는 곡선.
NACA 636183 에어포일의 드래그 곡선. 반대 플롯으로 색상으로 구분됩니다.

항공기 날개의 유의한 공기역학 특성은 두 가지 차원 없는 양, 즉 양력과 항력L 계수 C와D C로 요약된다.이러한 다른 공기역학적 양과 마찬가지로 이들은 공격각α만의 함수이며 레이놀즈수e R과 마하수 M.CL.CD.C.C는 α에 대해 플롯할 수도 있고 서로 [2][3]플롯할 수도 있다.

리프트와 견인력, L과 D는 C와D C를L 얻기 위해 동일한 인자에 의해 스케일링되므로 L/DL = CD/C이다.L과 D는 직각이며, D는 자유류 속도(주변 원거리 공기의 상대 속도)와 평행하기 때문에, 결과력 R은 그래프의 원점에서 대응하는L C, C점에D 이르는D 선과 같은 각도로 D에 놓인다.

풍동 내에서 공기역학적 표면이 일정한 공격각도로 유지되고 그 결과 발생하는 힘의 크기와 방향을 측정하면 극좌표를 이용하여 플롯할 수 있다.이 측정을 다른 공격 각도로 반복하면 드래그 곡선이 얻어집니다.리프팅 및 드래그 데이터는 1880년대에 Otto Lilienthal에 의해 수집되었고 1910년경 Gustav Effel에 의해 수집되었지만 보다 최근의 계수에 대해서는 제시되지 않았다.에펠은 "드래그 폴라"[4]라는 이름을 처음 사용했지만, 오늘날 극좌표를 사용하여 드래그 곡선을 그리지는 않습니다.

항공기 유형에 따라 다른 레이놀드와 마하 수치에서 항력 곡선을 그려야 할 수도 있다.전투기의 설계는 다른 마하 수에 대한 항력 곡선을 필요로 하는 반면, 서멀에서 또는 그들 사이에서 빠르게 비행하는 데 시간을 보내는 글라이더는 다른 레이놀즈 수에서 곡선을 필요로 할 수 있지만 압축성 효과의 영향을 받지 않는다.설계가 발전하는 동안 드래그 곡선은 정교해집니다.예를 들어 언더캐리지와 플랩 [2]배치 여부에 따라 특정 항공기는 동일한e R 및 M 값에서도 다른 곡선을 가질 수 있다.

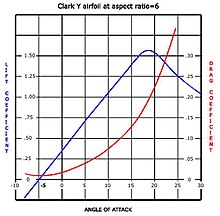
경비행기의 드래그 곡선.CD0 = 0.017, K = 0.075, CL0 = 0.1입니다.접선은 최대 L/D 점을 제공합니다.

첨부된 다이어그램은 일반적인 경비행기의 C 대 C를D 보여준다L.최소D C점은 그림에서 가장 왼쪽에 있습니다.항력의 한 가지 요소는 유도 항력(표시된 공기 속도를 증가시킴으로써 감소시킬 수 있는 리프트 생성의 불가피한 부작용)이다.이것은 C에L2 비례한다.다른 항력 메커니즘인 기생 및 파동 항력은 C에 비례하여L2 증가하는 일정한 성분, 총합D0 C 및 리프트 의존적 기여 모두를 가지고 있다.그럼 총합해서

CD = CD0 + K. (CL - CL0).2

C의 효과는L0 곡선을 그래프 위로 이동시키는 것이다. 이는 물리적으로 캠버 날개 또는 유한한 입사각과 같은 일부 수직 비대칭에 의해 발생하며, 이는 최소 드래그 자세가 양력을 생성하고 최대 리프트 대 [2][5]드래그 비율을 증가시킨다.

전력 필요 곡선

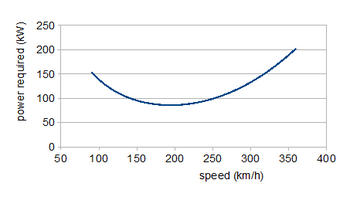
설계 프로세스에서 곡선이 사용되는 방법의 한 가지 예는 작동 속도 범위에 걸쳐 안정적인 수평 비행에 필요한 동력을 표시하는 데 필요한 동력R(P) 곡선의 계산이다.관련된 힘은 계수에서 (θ/2)를 곱하여 구한다.여기서2 θ는 비행 고도에서의 대기의 밀도이며, S는 날개 면적, V는 속도이다.수평 비행에서, 양력은 무게 W와 같고 추력은 항력과 같기 때문에,

날개R 면적 15m², 프로펠러 효율 0.8의 드래그 곡선을 초과하고 무게가 2000kg인 경비행기의 P 곡선.
W = (120/2).S.V2.CL 및
PR = (1200/2µ).SVC3D

두 번째 등식에서 프로펠러 효율과 함께 V/m2의 추가 인자는 P=(요구 추력)×V/m2이므로R 입력된다.추진력보다는 동력이 프로펠러 구동 항공기에 적합하며, 이는 제트 엔진이 일정한 추력을 생성하기 때문이다.무게가 일정하기 때문에 이들 방정식의 첫 번째에 의해 C가 속도가 증가할 때 어떻게L 하강하는지가 결정됩니다.드래그 곡선에서 C를 사용하여 이러한D CL 값을 두 번째 방정식에 대입하면 검정력 곡선이 생성됩니다.저속 영역은 리프트 유도 항력의 하락을 나타내며, 고속에서 프로필 항력의 증가가 뒤따른다.195km/h(121mph)의 속도에서 필요한 최소 출력은 약 86kW(115hp)이며, 최대 속도 300km/h(186mph)의 경우 135kW(181hp)가 필요합니다.최소 출력으로 비행하면 최대 내구성을 얻을 수 있습니다. 최대 범위는 전력 곡선에 접하는 부분이 원점을 통과하는 속도이며, 약 240km/h(150mph)[6]입니다.

곡선에 대한 분석식을 사용할 수 있는 경우, 미분화를 통해 유용한 관계를 개발할 수 있습니다.예를 들어 위의 형식은 C = 0으로 약간L0 단순화하면 C = CD0/K에서 최대LL2 C/C를D 갖는다.프로펠러 항공기의 경우 이는 최대 내구성 조건이며 185km/h(115mph)의 속도를 제공한다.해당하는 최대 범위 조건은 C= 3.CD0/K에서L2 C/C의L3/2D 최대값이며, 따라서 최적 속도는 244km/h(14mph)입니다.근사L0 C = 0의 효과는 5% 미만이다. 물론 유한L0 C = 0.1일 때 분석 및 그래픽 방법은 동일한 [6]결과를 나타낸다.

저속 비행 영역은 "힘 곡선의 후방"([7][8]때로는 "끌림 곡선의 후방")으로 알려져 있으며, 더 느리게 비행하기 위해 더 많은 동력이 필요합니다.속도가 증가하고 출력이 감소하기 때문에 비행의 비효율적인 영역입니다. 증가된 속도와 증가된 전력 소비 사이에는 균형이 없습니다.

상승률

항공기가 각도 θ 및 속도 V에서 상승하려면 엔진은 수평 비행 시 해당 속도에서 경험하고 동력 요구 그래프에 표시된 항력의 균형을 맞추기 위해 필요한R 동력 P를 초과하여 더 많은 동력 P를 개발해야 한다.수평 비행에서는R P/V = D이지만 상승에서는 다음과 같은 추가 중량 요소가 포함된다.

P/V = D + W.sin θ = PR/V + W.sin θ.

따라서 상승 속도 RC = V.sin δ = (P - PR)/W.[9]300km/h에서 최대 속도에 필요한 135kW 엔진이 장착되었다고 가정할 때, 최대 초과 출력은 135 - 87 = P의 최소R 속도 및 2.4m/s 상승 속도에서 48Kw이다.

연비

프로펠러 항공기(터보프롭 포함)의 경우 최대 범위와 최대 연료 효율은 최대 리프트 대 드래그 비율의 속도로 비행함으로써 달성된다.이 속도는 주어진 연료량에 대해 가장 먼 거리를 주행하는 속도입니다.항력이 최소화되면 최대 내구성(공중 시간)이 낮은 속도에서 달성됩니다.

제트 항공기의 경우 최대 내구성은 리프트 대 드래그 비율이 최대화될 때 발생한다.최대 범위는 고속으로 발생합니다.제트엔진은 동력생산이 아닌 추력생산을 하기 때문이다.터보프롭 항공기는 터빈 배기 가스를 통해 약간의 추력을 발생시키지만, 대부분의 출력은 프로펠러를 통해 동력을 발생시킨다.

"장거리 순항" 속도(LRC)는 일반적으로 최대 범위 속도보다 1% 낮은 연료 효율을 제공하도록 선택되는데, 이는 속도가 3~5% 증가하기 때문이다.그러나 연료는 항공사 운영에서 유일한 한계 비용이 아니므로 대부분의 경제 운영 속도(ECON)는 연료 [10]비용에 대한 시간 비용 비율인 비용 지수(CI)에 기초하여 선택된다.

글라이더

같은 항공기에 동력이 없다.접선은 최대 범위에 대한 최소 활공 각도를 정의합니다.곡선의 피크는 최대 내구성을 위한 최소 싱크 속도를 나타냅니다(공중 시간).

동력 없이 활공하는 항공기는 그것을 추진하기 위한 중력만 가지고 있다.활공각 θ에서 중량은 비행선에 대한 직각에서의 W.cos θ와 그에 평행한 W.sin θ의 두 가지 성분을 가진다.이들은 각각 힘과 리프트 구성 요소에 의해 균형을 이룹니다.

W.cos θ = (1200/2).S.V2.CL 및
W. sin = （ / / 2 ）S.V2.CD.

하나의 방정식을 다른 방정식으로 나누면 활공각은 tan θD = C/C로L 나타납니다.동력 공급되지 않은 비행에서 가장 관심 있는 성능 특성은 지상을 가로지르는 속도g, 예를 들어 V와 싱크 속도s V이다. 이러한 특성은 V.cos = V에 대한s V.sin = V.cos = V에g 대한 플롯으로 표시된다. 이러한 플롯을 일반적으로 폴라(polar)라고 하며 V의 함수로서 활공각도가 필요하다.[11]

두 힘의 방정식에 대한 해법을 찾는 한 가지 방법은 둘 다 제곱한 다음 합산하는 것입니다. 이것은 가능한L C, CD 값이 반지름 2의 원 위에 있음을 나타냅니다.W/S.V2.드래그 폴러에 플롯하면 두 곡선의 교차점에서 솔루션과 그 θ 값이 판독됩니다.또는 일반적으로 활공은 얕다는 점을 염두에 두고 10° 미만인 근사 cos θ 1을 리프트 방정식과 산출된 선택 V에 대해 C의 값에L 사용하여 드래그 극에서 C를 구한L 후 [11]θ를 산출할 수 있다.

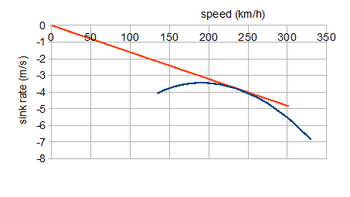
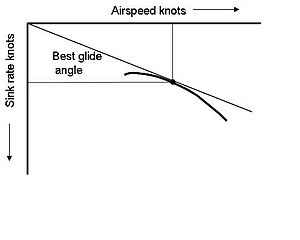
여기에서 극성은 위에서 분석한 항공기의 항력 극성이 정지된 프로펠러에 의해 크게 변화하지 않는다고 가정할 때 활공 성능을 보여준다.원점에서 곡선상의 어떤 점까지의 직선은 그 속도에서의 활공각과 같은 구배를 가지므로 대응하는 접선은 최적의 활공각−1 tan(CD/CL)min 3 3.3°를 나타낸다.이 속도는 최저 싱크 속도는 아니지만 240km/h(149mph)의 속도를 필요로 하는 최대 범위를 제공합니다. 약 3.5m/s의 최소 싱크 속도는 180km/h(112mph)로, 이전의 동력 [11]플롯에서 볼 수 있는 속도입니다.

싱크 레이트

대기 속도가 증가하면 전체 항력이 감소했다가 증가합니다.
최소 싱크 레이트에 대한 활공각을 나타내는 활공기의 극곡선.그래프의 원점은 대기 속도 축이 0 및 싱크 속도 0에서 싱크 속도 축과 교차하는 지점입니다.수평선은 극곡선의 맨 위에 접선합니다.이 접선점은 최소 싱크 공기 속도(수직선)를 나타냅니다.싱크 레이트는 이 포인트의 왼쪽 또는 오른쪽으로 증가하며, 저속 또는 고속에 대응합니다.이 최소 싱크 대기 속도는 싱크 속도가 가장 낮으며 착륙 [12][13]전 가능한 가장 긴 활공 시간을 허용한다.
최적의 활공 속도(최고의 L/D)를 위한 활공각을 나타내는 활공기의 극곡선.이는 조용한 공기를 통해 가능한 가장 평평한 활공각으로 비행 거리를 극대화합니다.이 속도(수직선)는 그래프의 원점에서 시작하는 선의 접점에 해당합니다.이 속도보다 빠르거나 느리게 비행하는 글라이더는 [13][12]착륙하기 전에 더 적은 거리를 주행할 수 있습니다.

항공기(일반적으로 글라이더)의 대기 속도에 대한 싱크 속도를 보여주는 그래프를 극곡선이라고 [13]합니다.극곡선은 글라이더의 최소 싱크 속도, 최량 드래그(L/D) 및 [12]비행 속도를 계산하는 데 사용됩니다.

글라이더의 극곡선은 이론적인 계산이나 다양한 공기 속도에서의 싱크 속도를 측정하여 도출됩니다.그런 다음 이러한 데이터 점을 선으로 연결하여 곡선을 형성합니다.각 타입의 글라이더는 독특한 극곡선을 가지고 있으며, 각각의 글라이더는 날개의 평활도, 제어 표면 항력, 날개에 벌레, 먼지, 비의 유무에 따라 다소 다르다.예를 들어 단독 대 이중 비행, 워터 밸러스트 유무, 플랩 설정 또는 날개 끝 확장 [13]유무와 같은 다양한 글라이더 구성은 서로 다른 극곡선을 가진다.

최고의 비행 속도를 아는 것은 글라이더의 성능을 이용하는데 중요하다.활공기의 성능의 두 가지 주요 척도는 최소 싱크 레이트와 최고의 활공비이며, 이는 "최고의 활공각"으로도 알려져 있습니다.이것들은 다른 속도로 발생합니다.이러한 속도를 아는 것은 효율적인 크로스컨트리 비행을 위해 중요합니다.정지된 공기에서 극곡선은 최소 싱크 속도로 비행하는 것이 조종사가 가능한 한 오랫동안 공중에 머물 수 있고 가능한 한 빠르게 상승할 수 있음을 나타내지만, 이 속도에서 활공기는 최상의 활공을 위해 속도로 비행하는 것처럼 멀리 이동하지 않습니다.

바람, 양력/침하 및 중량이 최적의 활공 속도에 미치는 영향

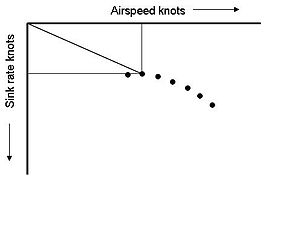
역풍으로 비행할 수 있는 최적의 속도는 역풍 속도에 따라 수평축을 따라 원점을 오른쪽으로 이동하고 새로운 접선을 그려 그래프에서 결정됩니다.이 새로운 비행 속도는 역풍이 증가할수록 빨라지지만, 도달 거리가 가장 길어집니다.일반적으로 최대 거리를 위한 최적의 L/D에 역풍 구성요소의 절반을 추가하는 것이 일반적입니다.순풍의 경우 순풍의 속도에 따라 원점이 왼쪽으로 이동하고 새 접선 선을 그립니다.순풍 속도는 최소 싱크대와 최적 L/[13]D 사이에 있습니다.

침하공기에서는 기단싱크 레이트에 따라 극곡선을 낮게 이동시켜 새로운 접선을 그린다.이것은 가라앉은 공기에서 더 빨리 비행해야 한다는 것을 보여줄 것이고, 이는 가라앉은 공기가 글라이더의 고도를 낮출 시간을 줄인다.이에 따라 극곡선은 상승률 및 새로운 [12]접선에 따라 위쪽으로 변위한다.

중량의 증가는 활공 항공기의 최대 범위에 영향을 미치지 않는다.활공각은 리프트/드래그 비율에 의해서만 결정됩니다.중량이 증가하면 최적의 활공각을 유지하기 위해 비행속도가 증가해야 하므로 무거운 활공기는 최적의 활공경로를 따라 더 빠른 [14]속도로 하강하기 때문에 내구성이 저하됩니다.

「 」를 참조해 주세요.

외부 링크

  • Glider Performance Airspeeds 기본 극곡선에 대한 애니메이션 설명으로, 침하 또는 상승 공기와 역풍 또는 후풍에 대한 수정 사항을 포함합니다.

레퍼런스

  1. ^ Shames, Irving H. (1962). Mechanics of Fluids. McGraw-Hill. p. 364. LCCN 61-18731. Retrieved 8 November 2012. Another useful curve that is commonly used in reporting wind-tunnel data is the CL vs CD curve, which is sometimes called the polar plot.
  2. ^ a b c Anderson, John D. Jnr. (1999). Aircraft Performance and Design. Cambridge: WCB/McGraw-Hill. ISBN 0-07-116010-8.
  3. ^ Abbott, Ira H.; von Doenhoff, Albert E. (1958). Theory of wing sections. New York: Dover Publications. pp. 57–70, 129–142. ISBN 0-486-60586-8.
  4. ^ Aircraft Performance and Design. p. 139.
  5. ^ Aircraft Performance and Design. pp. 414–5.
  6. ^ a b Aircraft Performance and Design. pp. 199–252, 293–309.
  7. ^ "Proficiency: Behind the power curve". 11 May 2013.
  8. ^ "Behind the Curve". 4 November 2002.
  9. ^ Aircraft Performance and Design. pp. 265–270.
  10. ^ "AERO - Fuel Conservation Strategies: Cruise Flight". www.boeing.com. Boeing. Retrieved 28 January 2022.
  11. ^ a b c Aircraft Performance and Design. pp. 282–7.
  12. ^ a b c d Wander, Bob (2003). Glider Polars and Speed-To-Fly...Made Easy!. Minneapolis: Bob Wander's Soaring Books & Supplies. p. 7-10.
  13. ^ a b c d e Glider Flying Handbook, FAA-H-8083-13A. U.S. Department of Transportation, FAA. 2013. p. Chapter 5, Pg 8. ISBN 9781619541047.
  14. ^ "Glide Performance - SKYbrary Aviation Safety". 25 May 2021.