동전회전 역설

Coin rotation paradox
외부 코인은 내부 코인을 한 바퀴 돌게 합니다.
움직이는 동전의 가장자리에 있는 한 점의 경로는 심장병입니다.

동전 회전 역설은[citation needed] 같은 크기의 다른 동전의 테두리에 하나의 동전을 굴리면, 외부의 기준틀에서 보았을 때, 움직이는 동전이 정지해 있는 동전을 끝까지 돌고 나서 한 개가 아니라 두 개의 완전한 회전을 완성한다는 반직관적인 관찰입니다.[1]

묘사

두 개의 동일한 동전이 테이블 위에서 서로 맞닿는 것부터 시작하여 "머리" 면이 표시되고 평행합니다. 동전 A를 정지시킨 상태에서 동전 B를 A 주위로 회전시키면서 미끄러짐 없이 접점을 유지합니다. 동전 B가 반대쪽에 도달하면, 두 개의 머리는 다시 평행이 될 것입니다. B는 한 번의 회전을 했습니다. 계속해서 B를 움직이면 다시 시작 위치로 되돌아오고 두 번째 회전이 완성됩니다. 역설적이게도 동전 B는 둘레의 두 배에 해당하는 거리를 굴린 것으로 보입니다. 실제로는 두 동전의 둘레가 같기 때문에 정의상 동전 B는 자신의 둘레와 같은 거리만 굴렸습니다. 두 번째 회전은 그것이 굴러온 경로가 원이라는 사실에서 비롯됩니다. 이것은 단순히 코인 B를 "상황에서" 회전시키는 것과 유사합니다.

효과를 시각화하는 한 가지 방법은 동전 A의 둘레를 "평탄하게" 직선으로 상상하는 것인데, 이를 통해 동전 B가 현재 평평한 경로를 따라 이동할 때 한 번만 회전하는 것을 관찰할 수 있습니다. 이게 '1회전'입니다. 마찬가지로, 현재의 특정 접점을 유지하면서 동전 A의 둘레에 동전 B를 미끄러뜨리는 것 대신 원래 시나리오에서 "2차 회전"을 나타내는 회전을 제공합니다.

동전 B가 회전할 때, 동전 둘레의 각 점은 심장 곡선을 묘사합니다.

분석 및 솔루션

처음부터 끝까지 움직이는 동전의 중심은 원형의 경로를 이동합니다. 정지된 동전의 둘레와 중심의 경로는 두 개의 동심원을 형성합니다. 바깥쪽 원의 반지름은 동전의 반지름의 합이므로, 움직이는 중심의 경로의 원둘레는 동전의 두 배입니다.[2] 움직이는 동전의 중심은 동전 둘레의 두 배를 미끄러지지 않고 이동하기 때문에 움직이는 동전은 두 번의 완전한 회전을 합니다.[3]

움직이는 동전이 있는 경우, 그것의 중심을 중심으로 회전하는 양(시계방향, 반시계방향, 또는 둘 중 일부)은 경로의 길이에 영향을 미치지 않습니다. 동전이 위에서 설명한 것처럼 두 번 회전하고 고정된 동전에 닿으면서 움직이는 동전의 가장자리에 집중하는 것은 주의를 산만하게 합니다.

반지름 및 기타 모양이 같지 않음

R = 3r인 경우의 예. 그림 1에서 R을 편 상태에서 회전 수(화살이 이후 위쪽을 가리키는 횟수)는 R/r = 3입니다. 그림 2에서 R이 원으로 복원되었기 때문에 동전은 추가 회전을 하여 R/r + 1 = 4가 됩니다. (애니메이션)
작은 동전이 큰 동전을 중심으로 회전하는 것

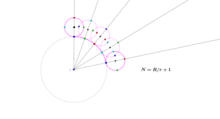
반지름 R 중 하나를 둘러싼 반지름 r의 동전은 R/r + 1 회전을 만듭니다.[4] 그것은 롤링 코인의 중심이 R + r/r = R/r + 자신의 반지름(또는 원둘레)의 1배인 원형 경로를 이동하기 때문입니다. R = 0일 때, 반지름이 r인 동전은 바닥점을 중심으로 0/r + 1 = 1 단순 회전을 합니다.

1982년 5월 1일 SAT에서 이 문제에 대한 질문이 있었고, 인간의 실수로 인해 3명의 학생들이 선택지 중 정답이 없다는 것을 증명한 후에 다시 채점해야 했습니다.[5][6]

동전이 굴러가는 모양은 원일 필요가 없습니다. 자신과 교차하지 않는 단순한 다각형이나 폐곡선일 때 한 번의 추가 회전이 둘레의 비율에 더해집니다. 모양이 복잡할 경우 추가된 회전 수(또는 동전이 곡선 내부에서 구르는 경우 차감)가 회전 수의 절대값입니다.

적용들

패러독스는 사이드 리얼 타임과 관련이 있습니다. 사이드 리얼 데이는 지구가 회전하여 먼 별이 하늘의 같은 위치로 돌아오는 데 걸리는 시간인 반면, 태양일은 태양이 같은 위치로 돌아오는 시간입니다. 1년은 약 365.25일의 태양일을 갖지만, 366.25일은 태양 주위를 도는 한 번의 공전을 설명하기 위한 부수적인 날입니다.[7] 태양일은 24시간이므로, 측면일은 약 365.25/366.25 × 24시간 = 23시간 56분 4.1초입니다.

퍼즐의 버전은 군 이론, 특히 G의2 분할 실수 형태로 알려진 Lie 군에 대한 연구에서 발생합니다. 이 집단의 한 구성은 반지름이 3배인 다른 공 주위를 굴러다니는 공이 3번이 아니라 4번이나 완전히 회전한다는 사실을 이용합니다.[8]

참고 항목

참고문헌

  1. ^ Weisstein, Eric W. "Coin Paradox". MathWorld.
  2. ^ Bunch, Bryan H. (1982). Mathematical Fallacies and Paradoxes. Van Nostrand Reinhold. pp. 10–11. ISBN 0-442-24905-5.
  3. ^ "Rotational dynamics - Center of wheel travels the length of circumference in one revolution".
  4. ^ Talwalkar, Presh (July 5, 2015). Everyone Got This SAT Math Question Wrong. MindYourDecisions – via YouTube.
  5. ^ "Error found in S.A.T. question". The New York Times. United Press International. May 25, 1982. ISSN 0362-4331. Retrieved February 9, 2021.
  6. ^ Muller, Derek (November 30, 2023). The SAT Question Everyone Got Wrong. Veritasium – via YouTube.
  7. ^ 바틀렛, A. K., 태양과 사이드리얼 타임, 대중천문학, vol. 12, 페이지 649-651
  8. ^ Baez, John C.; Huerta, John (2014). "G2 and the Rolling Ball". Transactions of the American Mathematical Society. 366 (10): 5257–5293. arXiv:1205.2447. Bibcode:2012arXiv1205.2447B. doi:10.1090/S0002-9947-2014-05977-1. MR 3240924.

더보기

  • Gardner, Martin (1975). "Penny Puzzles". Mathematical Carnival. Alfred A. Knopf.

외부 링크

이 투표된 답에는 애니메이션과 "외부 동전"의 r이 내부 동전의 반지름의 1/3인 원래 질문에 대한 직관적인 설명이 포함되어 있습니다.