바쁜 비버

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다. 기술적인 내용을 삭제하지 않고 비전문가도 쉽게 이해할 수 있도록 개선해 주시기 바랍니다. (2016년 10월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인) 이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정확한 인용문을 도입하여 이 기사의 개선에 도움을 주시기 바랍니다. (2013년 2월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

이론 컴퓨터 과학에서, 바쁜 비버 게임은 가능한 ^[1]가장 많은 출력을 내는 주어진 크기의 종료 프로그램을 찾는 것을 목표로 한다.무한출력을 내는 무한루프 프로그램은 쉽게 구상할 수 있기 때문에 이러한 프로그램은 게임에서 제외된다.

좀 더 정확히 말하면, 바쁜 비버 게임은 주어진 상태 집합만을 사용하여 테이프에 가장 많은 1s를 쓰는 알파벳 {0,1}으로 정지하는 튜링 기계를 설계하는 것으로 구성됩니다.2스테이트 게임의 규칙은 다음과 같다.

1. 기계는 정지 상태 외에 두 가지 상태를 가져야 합니다.
2. 테이프에는 처음에는 0만 포함되어 있습니다.

플레이어는 테이프의 가장 긴 출력인 1s를 목표로 하는 이행 테이블을 구상하면서 머신이 최종적으로 정지하는 것을 확인해야 합니다.

n번째 바쁜 비버, BB-n 또는 단순히 "바쁜 비버"는 n번째 주의 바쁜 비버 게임에서 승리하는 튜링 기계입니다.즉, 가능한 모든 n-상태 경쟁 튜링 기계 중에서 가장 많은 1s를 획득합니다.예를 들어 BB-2 튜링 기계는 6단계에 걸쳐 4개의 1을 달성한다.

임의의 튜링 기계가 바쁜 비버인지 아닌지는 판단할 수 없습니다.이것은 계산 가능성 이론, 정지 문제 및 복잡성 이론과 관련이 있습니다.이 개념은 티보르 라도가 1962년 발표한 논문 "계산 불가능한 함수에 대하여"^[1]에서 처음 소개되었습니다.

게임

1962년 Tibor Rado의 논문에 소개된 n-state busy bever 게임(또는 BB-n 게임)은 튜링 기계 클래스를 포함하고 있으며 각 구성원은 다음 설계 사양을 충족해야 합니다.

• 머신에는 n개의 "작동 가능한" 상태와 Halt 상태가 있습니다.여기서 n은 양의 정수이며 n개의 상태 중 하나가 시작 상태로 구분됩니다.(통상, 스테이트는 1, 2, ..., n, 스테이트 1을 개시 스테이트, 또는 스테이트 A를 개시 스테이트로서 A, B, C, ... 로 라벨이 붙여집니다).
• 기계는 단일 양방향 무한(또는 무제한) 테이프를 사용합니다.
• 테이프 알파벳은 {0,1}이며 0은 공백 기호로 사용됩니다.
• 기계의 전환 기능은 두 가지 입력을 받습니다.

1. 현재 비할트 상태,
2. 현재 테이프 셀의 기호,

3개의 출력을 생성합니다.

1. 현재 테이프 셀의 기호를 덮어쓸 기호(덮어쓰기 기호와 동일한 기호일 수 있음),
2. 이동하는 방향(좌 또는 우, 즉 현재 셀의 왼쪽 또는 오른쪽으로 한 자리씩 테이프 셀로 이동) 및
3. 이행하는 상태(Halt 상태일 수 있음)

따라서 (4n + 4)²ⁿ개의 n-상태 튜링 기계가 이 정의를 만족하는 이유는 공식의 일반 형식이 (기호 × 방향 × (상태 + 1)^{(symbols × states)}이기 때문이다.

전이 함수는 5-튜플의 유한 테이블로 볼 수 있으며, 각 형태는

(현재 상태, 전류 기호, 쓸 기호, 이동 방향, 다음 상태).

기계는 시작 상태에서 시작하여 현재 테이프 셀이 공백(모두 0) 테이프의 셀인 후 Halt 상태가 될 때까지 전환 기능을 반복하는 것으로 구성됩니다.머신이 최종적으로 정지했을 경우에만 테이프에 남아 있는 1의 수를 머신의 스코어라고 부릅니다.

n-state busy bever (BB-n)게임은 가장 큰 점수를 가진 n-state turing 머신을 찾기 위한 경연대회입니다.-정지 후 테이프에서 가장 많은 1s를 얻습니다.모든 n-상태 튜링 기계 중에서 가장 큰 점수를 획득하는 기계를 n-상태 비버라고 하며, 점수가 지금까지 획득된 것 중 가장 높은 것(아마 가장 큰 것은 아닐 수도 있음)을 챔피언 n-상태 기계라고 한다.

Rado는 콘테스트에 응모한 각 머신에 Halt 상태에 도달하기 위해 필요한 정확한 스텝 수를 기술할 것을 요구했습니다.따라서 (원칙적으로) 각 엔트리의 스코어는 지정된 스텝 수만큼 기계를 실행함으로써 검증할 수 있습니다. (엔트리가 머신 설명만으로 구성되어 있는 경우)모든 잠재적인 엔트리가 판별할 수 없는 것을 확인합니다.이는 이미 알려진 정지 문제와 같기 때문입니다.즉, 임의의 머신이 최종적으로 정지할지를 결정하는 효과적인 방법은 없습니다.)

관련 기능

비지 비버 함수 δ

비지 비버 함수는 비지 비버가 주어진 측정값에서 얻을 수 있는 최대 점수를 수량화합니다.이것은 계산할 수 없는 함수입니다.또, 비지 비버 함수는, 계산 가능한 ^[2]함수보다 점근적으로 고속으로 성장하는 것을 나타낼 수 있다.

비지 비버 함수인${\displaystyle \delta \mathbb{}}$ : N $→$ ${\displaystyle N\mathbb{}}$ {\$displaystyle \Sigma :\mathbb {N}$ \$to$ \$mathbb {N}$$}$은 공백 타입에서 모든 정지된 2-n 상태 튜링 기계 중 δ(n)가 달성 가능한 최대 점수(테이프 상의 최대 수)가 되도록 정의됩니다.

δ가 잘 정의된 함수인 것은 분명하다: 매 n에 대하여, 위와 같이 기껏해야 많은 n-상태 튜링 기계가 존재하며, 따라서 기껏해야 많은 가능한 실행 시간이 존재한다.

이 무한 수열 δ는 비버 함수이며, δ(M) = δ(n) (즉, 최대 점수를 획득하는) 모든 n-상태 2-비버 튜링 기계 M을 비버라고 한다.각 n에는 적어도 4개의 n-상태 비버가 존재합니다(n-상태 비버가 주어졌을 때 다른 비버는 정지된 천이에서 이동 방향을 변경하는 것만으로 얻을 수 있고, 다른 비버는 모든 방향 변경을 반대 방향으로 이동하는 것으로 얻을 수 있으며, 마지막은 모두 스왑된 비버의 정지 방향을 이동하는 것으로 얻을 수 있습니다).

계산 불가

Rado의 1962년 논문은 f${\displaystyle }$: ${\displaystyle N\mathbb{}}$ ${\displaystyle \to }$ {\$displaystyle$ f$:\mathbb {N}$ \$to$ \$mathbb {N}}$이 계산 가능한 함수라면 충분히 큰 모든 n에 대해 δ(n) > f(n)이므로 δ는 계산 가능한 함수가 아님을 증명했다.

게다가 이것은 임의의 튜링 기계가 바쁜 비버인지 아닌지는 일반적인 알고리즘으로 판단할 수 없다는 것을 암시한다. (그런 알고리즘은 존재할 수 없다. 왜냐하면 그 존재는 증명된 불가능인 δ를 계산할 수 있기 때문이다.)특히, 그러한 알고리즘은 다음과 같이 δ를 계산하는 다른 알고리즘을 구성하는데 사용될 수 있다: 주어진 n에 대해, 각각의 n-상태 2-심볼 튜링 기계는 n-상태 비버가 발견될 때까지 테스트될 것이다; 그리고 이 비지 비버 기계는 정의 δ(n)에 따라 점수를 결정하기 위해 시뮬레이션될 것이다.

δ(n)는 계산할 수 없는 함수이지만, 그 값을 취득해, 그 값이 올바른 것을 증명할 수 있는 작은 n이 몇개 있습니다.δ(0) = 0, δ(1) = 1, δ(2) = 4라는 것을 나타내는 것은 어렵지 않으며, 점차적으로 δ(3) = 6 및 δ(4) = 13(OEIS의 시퀀스 A028444는 N을 가지지 않음)이라는 것을 알 수 있다.

2016년 Adam Yedidia와 Scott Aaronson은 ZFC에서 δ(n)가 증명 불가능한 최소 n의 첫 번째(명시적) 상한을 구했다.그렇게 하기 위해 그들은 합리적인^[3] 일관성 가설(정적 램지 특성)^[4][5] 하에 7910-상태 튜링 기계를 구성했다.이것은 후에 1919년 주로 축소되었고, 램지의 정지된 재산에 대한 의존성은 ^[6][7]사라졌고, 나중에는 748개 ^[8]주로 줄었다.

σ의 복잡성과 실현 불가능성

Kolmogorov 복잡도의 변형은 다음과 같이 정의됩니다 [cf].Boolos, Burgess & Jeffrey, 2007년]:숫자 n의 복잡도는 BB급 튜링 기계가 처음에 빈 테이프에서 n개의 연속된 1s의 단일 블록으로 정지하는 데 필요한 최소 상태 수입니다.차이틴의 불완전성 정리의 해당 변형은 자연수에 대한 주어진 공리 시스템의 맥락에서, 어떤 특정한 수가 k보다 큰 복잡성을 가지고 있다는 것을 증명할 수 없는 수 k가 존재하며, 따라서 어떠한 특정한 상한도 δ(k)에 대해 증명될 수 없다는 것을 말한다."n > δ(k)"가 증명된 경우 n은 k보다 크다.인용된 참고문헌에서 언급되었듯이, "수학적 수학"의 공리체계에 대해 이것이 참인 최소값 k는 10↑↑10보다 훨씬 작습니다. 따라서, 일반 수학의 맥락에서, 값이나 δ(10↑↑10)의 상한을 증명할 수 없습니다. (Gödel의 첫 번째 불완전성 정리는 다음과 같습니다.보통 수학의 공리 체계 n은 "σ(10 ↑↑ 10) = n" 형식의 참이지만 입증할 수 없는 문장이 있고, "10(10 ↑↑ 10) < n" 형식의 참이지만 입증할 수 없는 문장이 무한히 많다.

최대 변속 함수 S

함수 δ 외에, Rado[1962]는 튜링 기계의 BB급에 다음과 같이 정의된 또 다른 극한 함수인 최대 이동 함수 S를 도입했다.

• s(M) = M이 정지하기 전에 수행하는 이동 횟수. 임의의 M µ_n E에 대해,
• S(n) = max{s(M) M ∈ E_n} = 정지하는 모든 n-상태 2-스위치 튜링 기계에 의해 이루어진 가장 큰 수의 이동.

이러한 튜링 기계는 각각의 전환 또는 "단계"에서 시프트가 필요하기 때문에 최대 시프트 함수는 동시에 최대 단계 함수이다.

Rado는 S가 계산불능인 것과 같은 이유로 계산불능임을 보여주었습니다.즉, S는 계산불능함수보다 빠르게 성장합니다.그는 각 n에 대해 S(n) ≥ σ ( n(n)이라는 점을 언급함으로써 이를 증명했다.각 시프트는 테이프에 0 또는 1을 쓸 수 있는 반면, δ는 1을 쓴 시프트의 서브셋, 즉 튜링 기계가 정지했을 때 덮어쓰지 않은 시프트의 서브셋을 센다. 결과적으로, S는 적어도 계산 가능한 함수보다 더 빨리 성장한다는 것이 증명되었다.

δ와 S 사이의 다음의 연결은 Lin & Rado[튜링 기계 문제의 컴퓨터 연구, 1965년]가 δ(3) = 6이라는 것을 증명하기 위해 사용하였습니다: 주어진 n에 대하여, 만약 S(n)가 알려진다면, 모든 n-상태 튜링 기계는 원칙적으로 아직 그 지점에서 S(n) 단계까지 실행될 수 있습니다.이 때 테이프에서 가장 많은 1s로 정지한 기계(즉, 비버)를 관찰함으로써 테이프에서 δ(n)의 값을 얻을 수 있습니다.Lin & Rado가 n = 3의 경우에 사용한 접근방식은 S(3) = 21이라고 추측한 다음 최대 21단계에 걸쳐 본질적으로 다른 모든 3상태 기계를 시뮬레이션하는 것이었다.그들은 21단계 이내에 정지하지 않은 기계의 동작을 분석함으로써 그러한 기계들 중 어느 것도 정지하지 않을 것이라는 것을 보여주는데 성공하였고, 따라서 방금 설명한 절차에 의해 S(3) = 21이라는 추측을 증명하고 δ(3) = 6이라는 결론을 내렸다.

δ 및 S와 관련된 부등식은 다음을 포함한다([Ben-Amram, et al., 1996] 참조). 이들은 모든 n ≤ 1에 유효하다.

${\displaystyle\begin{aligned}S(n)&\Sigma(n)&\leq(2n-1)&\leq(3n+3)&<\Sigma(3n+6)&\end{aligned}}$

및 점근적으로 개선된 경계([Ben-Amram, Petersen, 2002]): 상수 c가 존재하기 때문에 모든 n≤ 2에 대해

$\displaystyle S(n)\leq \Sigma \left(n+\left\lceil {8n}{log _{2}n}}\right\rceil +c\right).}$

${\displaystyle S}$${\displaystyle }$(${\displaystyle n}$ )$${ $displaystyle$$S$ ($n$ )$$${\displaystyle (}$ （${\displaystyle }$n$$）의 제곱에 가까운 $경향$이 있습니다.실제로 많은${\displaystyle }$머신에서는${\displaystyle S}$ ($$n )는${\displaystyle {}^{}}$(${\displaystyle 2}$ ( n$$){ $displaystyle$\$Sigma$ $^ 2$($$n $)$보다 $작습니다{\displaystyle }$.

δ 및 S에 대해 알려진 값

2016년 현재 δ(n)와 S(n)의 함수 값은 정확히 n < ^[5]5에 대해서만 알려져 있다.

현재의 (2018년 현재) 5개 주 비버 챔피언은 47176870 스텝(1989년 하이너 마르크센과 위르겐 분트록에 의해 발견됨)을 사용하여 4098 1s를 생산하지만, 결코 멈추지 않는 것으로 생각되지만, 무한히 실행되는 것으로 증명되지 않은 비정규 동작을 가진 기계가 18개 또는 19개 남아 있다.골격 목록은 42 또는 43개의 검증되지 않은 기계이지만 ^[9]24개는 이미 검증되었습니다.나머지 기계들은 818억 단계로 시뮬레이션되었지만, 어느 것도 멈추지 않았다.대니얼 브릭스는 또한 ^[10]몇 가지 기계를 증명했다.또 다른 소식통은 98대의 기계는 아직 검증되지 않았다고 말한다.홀드아웃에 ^[11]대한 분석이 있습니다.따라서 δ(5) = 4098, S(5) = 47176870일 가능성이 높지만 이는 아직 입증되지 않았으며, 홀드아웃이 남아 있는지 여부(2018년 기준)도 알 수 없다.현재 6개 주 챔피언은 7.412×10³⁶⁵³⁴ 스텝(2010년 Pavel Kropitz에 의해 발견됨)을 사용하여 3.5147495×10¹⁸²⁶⁷ 1s 이상(정확히 (25³⁰³⁴¹×4+23)/9)을 생산하고 있습니다.위에서 설명한 바와 같이, 이것들은 2심볼 튜링 기계입니다.

6스테이트 머신의 단순한 확장으로 테이프에 10초 이상의 1을^{10101018705353} 쓸 수 있는 7스테이트 머신이 탄생하지만, 더 바쁜 7스테이트 머신은 의심의 여지없이 존재합니다.하지만, 다른 바쁜 비버 사냥꾼들은 다른 기계 세트를 가지고 있다.

밀턴 그린은 1964년 그의 논문 "이진 튜링 기계를 위한 라도의 시그마 함수에 대한 하한"에서 다음과 같은 것을 증명하는 튜링 기계 세트를 구성했다.

$\displaystyle \Sigma (2k)> 3\uparrow ^ {k-2,k-2)\qquad {mbox{ for }k\geq 2,}$

여기서 ↑는 Knuth 상향식 표기법이고 A는 Ackermann의 함수입니다.

따라서

$(\displaystyle \Sigma (10)>3\uparrow \uparrow 3=3\uparrow 3^{3^{3}}=3^{3^{3^{3^{}).^{.^{.^{3}}}}}}}$

(지수 타워에 3 = 7625597484987 항 포함³³),

$\displaystyle \Sigma (12)> 3\uparrow \uparrow \uparrow \uparrow 3=g_{1}.$

여기서 숫자₁ g는 Graham의 숫자를 정의하는 수열의 거대한 시작 값이다.

1964년 Milton Green은 스위칭 회로 이론과 논리 설계에 관한 1964년 IEEE 심포지엄에서 발표된 Busy Beaver 함수의 하한을 개발했습니다.하이너 마르크센과 위르겐 분트록은 그것을 "원시적 재귀가 아닌 사소하지 않은 하한"이라고 묘사했다.이 하한을 계산할 수 있지만 n의 관점에서 단일 식이라고 하기에는 너무 복잡합니다.n=8일 때, 이 방법은 δ(8) ( 3 × (7⁹² × 3 - 1) / 2 8 8.248×10이⁴⁴ 된다.

다음과 같은 전류 하한에서 도출할 수 있습니다.

$\displaystyle \Sigma ( 2k + 1)> 3\uparrow ^ {k-2,k-2)\qquad {}k\geq 2,}$

반면, δ(6)의 최적 전류 하한(2018년 기준)은 10으로¹⁸²⁶⁷, 그린 공식에 의해³ 주어진 하한(3 = 27)보다 크다(비교적으로 작음).실제로는 하한인 3 ↑↑ 3 = 3³³ = 3 = 7625597484987보다 훨씬 크며, 이는 Green의 첫 번째 하한인 3×(7×3-1⁹²)/2보다 훨씬 큽니다.

δ(7)는 동일한 방식으로 현재의 공통³¹ 하한 3(약 618조)보다 훨씬 크므로 두 번째 하한도 매우 약하다.

S(n) 및 δ(n)의 계산 불능 증명

S(n)가 계산 가능한 함수라고 가정하고 EvalS가 S(n)를 평가하는 TM을 나타내도록 합니다.n개의 1s 테이프가 있는 경우 테이프에 S(n) 1s가 생성되어 정지합니다.Let Clean은 테이프에 처음 기록된 1s 시퀀스를 청소하는 튜링 기계입니다.더블은 튜링 기계 평가 함수 n + n을 나타냅니다.n개의 1s를 가진 테이프가 주어진 경우 테이프에 2n 1s를 생성하고 나서 정지합니다.Double Evals Clean 구성을 만들고 n을 이 기계의₀ 상태 수로 합니다.Create_n은₀ 초기 빈 테이프에 n개의 1s를 작성하는₀ 튜링 머신을 나타냅니다.이 기계는 n개의 상태를 가지도록₀ 간단한 방식으로 구성될 수 있습니다(상태 i가 1을 쓰고 헤드를 오른쪽으로 이동하고 상태 i + 1로 전환함). 단, 정지하는₀ 상태 n은 제외합니다.N은 n + n의₀ 합이다₀.

Let BadS는 Create_n₀ Double Evals Clean 구성을 나타냅니다.이 머신에는 N개의 상태가 있습니다.첫 번째 빈 테이프로 시작하여 먼저 n개의 1s₀ 시퀀스를 만들고 두 배로 증가시켜 N개의 1s 시퀀스를 생성합니다.그 후 Bads는 테이프에 S(N) 1을 생성하고 최종적으로 모든 1을 클리어한 후 정지합니다.단, 클리닝 단계는 적어도 S(N) 스텝은 계속되기 때문에 BadS의 작업 시간은 S(N)보다 엄밀하게 길어 함수 S(n)의 정의에 반한다.

δ(n)의 계산불가능성은 유사한 방법으로 증명될 수 있다.위의 증명에서는 머신 EvalS를 Evalδ 및 Cleaning with Increment(단순한 TM)와 교환하여 테이프에서 첫 번째 0을 검색하여1로 치환해야 합니다.

S(n)의 부적합성은 공백 테이프의 정지 문제를 참조하여 확인할 수도 있습니다.빈 테이프의 정지 문제는 빈 테이프로 기동했을 때 정지할지를 튜링 머신에 대해 결정하는 문제입니다.공백 테이프의 정지 문제는, 표준의 정지 문제와 같기 때문에, 이것도 계산할 수 없습니다.만약 S(n)가 계산가능하다면, 우리는 단순히 S(n) 단계를 위해 n개의 상태를 가진 주어진 튜링 기계를 실행함으로써 빈 테이프의 정지 문제를 해결할 수 있다; 만약 그것이 여전히 정지되지 않았다면, 그것은 결코 해결되지 않을 것이다.따라서 공백테이프 정지 문제는 계산할 수 없기 때문에 S(n)도 마찬가지로 계산할 수 없습니다.

일반화

어떤 계산 모델에도 바쁜 비버의 단순한 유사점이 존재한다.예를 들어, n개의 상태와 m개의 기호를 가진 튜링 기계에 대한 일반화는 다음과 같은 일반화된 바쁜 비버 함수를 정의합니다.

1. δ(n, m): n-스테이트, m-심볼 머신에 의해 인쇄 가능한 비제로의 최대수.처음에는 공백테이프로 기동한 후 정지합니다.
2. S(n, m): n-상태, m-심볼 머신에 의해 행해진 스텝의 최대수.처음에는 공백테이프로 기동한 후 정지합니다.

예를 들어, 지금까지 발견된 가장 긴 3스테이트 3심볼 머신은 119112334170342540 스텝을 실행하고 나서 ^{[citation needed]}정지합니다.각 단계에서 테이프 값을 반전시키는 추가 특성이 있는 가장 오래 작동하는 6-스테이트, 2-심볼 기계는 47339970 ^{[citation needed]}단계 후에 6147 1s를 생성합니다.따라서 Reverse Turing Machine(^[12]RTM; 반전 튜링 머신) 클래스의 경우_RTM S(6) 47 47339970 및 σ_RTM(6) 6 6147이다.

비지 비버 함수를 두 개 이상의 차원으로 확장하여 더욱 일반화할 수 있습니다.

마찬가지로 레지스터 머신의 δ 함수에 대한 아날로그를 임의의 레지스터에 존재할 수 있는 최대수로 정의할 수 있습니다.이것은, 소정의 수의 명령에 대해서입니다.

정확한 값과 하한

다음 표에 일반화된 비버 문제에 대한 정확한 값과 S(n, m) 및 δ(n, m)의 알려진 하한을 나타냅니다.주의: "?"로 나열된 항목은 아래에서 왼쪽 위까지 모든 항목의 최대값으로 제한됩니다.이 기계들은 아직 조사되지 않았거나 더 작은 기계에 의해 추월되었다.

이러한 값을 달성하는 튜링 기계는 Wayback Machine 웹 페이지의 Pascal Michel의 Archived 2022-06-24에서 구할 수 있습니다.이들 웹사이트 각각은 튜링 기계의 분석과 정확한 값의 증명에 대한 참조도 포함하고 있다.

S(n, m) 값
n m	2스테이트	3스테이트	4스테이트	5스테이트	6스테이트
2개소켓	6	21	107	47176870?	> 10 $↑↑$ {\$displaystyle\uparrow\uparrow}$ 15$$
3소켓	38	© 119112334170342540	1.0×1014072 이상	?	?
4소켓	§ 3932964	5.2×1013036 이상	?	?	?
5소켓	1.9×10704 이상	?	?	?	?
6인치	2.4×109866 이상	?	?	?	?
δ(n, m) 값
n m	2스테이트	3스테이트	4스테이트	5스테이트	6스테이트
2개소켓	4	6	13	4098?	> 10 $↑↑$ {\$displaystyle\uparrow\uparrow}$ 15$$
3소켓	9	§ 374676383	1.3×107036 이상	?	?
4소켓	§ 2050	> 3.7×106518	?	?	?
5소켓	1.7×10352 이상	?	?	?	?
6인치	1.9×104933 이상	?	?	?	?

비결정적 튜링 기계

p-case, 2-state, 2-color^[13] NDTM에서의 최대 정지 시간과 상태

p	스텝	미국.
1	2	2
2	4	4
3	6	7
4	7	11
5	8	15
6	7	18
7	6	18

이 문제는 모든 분기 또는 가장 ^[13]긴 단계 수를 가진 분기에서 가장 많은 상태를 가진 시스템을 찾아 비결정론적 튜링 기계로 확장될 수 있습니다.특정 NDTM이 정지할지에 대한 질문은 여전히 계산상으로는 계산할 수 없으며, NDTM의 비버를 찾기 위해 필요한 계산은 결정론적인 경우보다 훨씬 큽니다.이는 고려해야 할 브랜치가 여러 개 존재하기 때문입니다.p개의 케이스 또는 규칙이 있는2가지 스테이트의 2색 시스템의 경우 오른쪽 표는 정지까지의 최대 스텝 수와 NDTM에 의해 작성된 최대 고유 스테이트 수를 나타냅니다.

적용들

다소 도전적인 수학 게임을 할 뿐만 아니라, 바쁜 비버 함수는 순수한 수학 문제를 풀 수 있는 완전히 새로운 접근 방식을 제공합니다.수학의 많은 미해결 문제들은 이론적으로는 풀 수 있지만 실제로는 풀리지 않는다. 충분히 큰 ^[14]n에 대한 S(n)의 값이 주어진다면.

셀 수 있는 수의 사례 중 반례를 통해 반증될 수 있는 추측(예: 골드바흐의 추측)을 고려한다.이 추측을 순차적으로 테스트하여 값을 증가시키는 컴퓨터 프로그램을 작성하십시오.Goldbach의 추측의 경우, 우리는 모든 짝수 θ 4를 순차적으로 고려하여 그것이 두 소수의 합인지 아닌지를 테스트한다.이 프로그램이 n-상태 튜링 기계에서 시뮬레이션된다고 가정합니다.반례(이 예에서는 2개의 소수점의 합이 아닌 짝수 4 4)를 발견하면, 반례는 정지해, 그것을 나타냅니다.그러나 추측이 사실이라면 우리의 프로그램은 중단되지 않습니다.(이 프로그램은 반례를 발견했을 경우에만 중지됩니다.)

이 프로그램은 n-상태 튜링 기계에 의해 시뮬레이트되므로 S(n)를 알면 기계를 그렇게 많은 단계로 작동시키는 것만으로 멈출지 여부를 결정할 수 있습니다.그리고 S(n) 단계 후에 기계가 정지하지 않는다면, 기계가 절대 정지하지 않을 것이며 따라서 주어진 추측에 대한 반례가 없다는 것을 안다(즉, 두 소수의 합이 아닌 짝수 없음).이것으로 추측이 사실임을 증명할 수 있을 것이다.

따라서 S(n)에 대한 특정 값(또는 상한)을 사용하여 수학의 많은 미해결 문제를 체계적으로 풀 수 있습니다(이론).단, 비버 비버 문제에 대한 현재 결과에 따르면 이는 두 가지 이유로 실용적이지 않습니다.

• 비지 비버 함수(및 최대 시프트 함수)의 값을 증명하는 것은 매우 어렵습니다.이것은 5개 이하의 상태의 초소형 머신에 대해서만 증명된 반면, 유용한 머신을 만들기 위해서는 적어도 20-50개의^{[citation needed]} 스테이트가 필요할 것으로 예상됩니다.게다가, 모든 알려진 S(n)의 정확한 값은 모든 n-상태 튜링 기계를 열거하고 각각의 정지 여부를 증명함으로써 증명되었다.S(n)가 실제로 유용하려면 직접적이지 않은 방법으로 S(n)를 계산해야 한다.
• 그러나 S(n)를 계산하는 더 나은 방법을 찾더라도 비지 비버 함수(및 최대 이동 함수)의 값은 매우 크고 매우 빠릅니다.S(6) > 10은³⁶⁵³⁴ 이미 시뮬레이션을 완료하기 위해 특별한 패턴 기반의 액셀러레이션이 필요합니다.마찬가지로 S(10) > 3(10) > 3 ↑↑↑ 3은 거대수이며, S(17) > > σ(17) > G는 Graham의 수이다.따라서 예를 들어 S(30)를 알고 있었다고 해도, 그 정도의 스텝수의 기계를 가동하는 것은 전혀 불합리하다.우주의 알려진 부분에는 S(6) 연산을 ^[15]직접 수행할 수 있는 계산 능력이 충분하지 않습니다.

주목할 만한 예

748 스테이트의 바이너리 튜링 머신은, ZFC가 ^[16]일관성이 없는 경우에 정지하는 것을 목적으로 하고 있습니다.744-상태 튜링 기계는 리만 가설이 ^[6][16]거짓일 경우 중단되는 것으로 구성되었다.골드바흐의 추측이 거짓일 경우 중지되는 43-상태 튜링 기계가 구축되었고, 그 추측에 대한 27-상태 기계는 제안되었지만 아직 ^[6][16]검증되지 않았다.

1979년에 Paul Erd's에 의해 공식화된 다음 추측이 거짓일 경우 15-상태 튜링 기계가 구성되었습니다: 모든 n > 8에 대해 ^[17][18]2의 기저ⁿ 3 표현에 적어도 하나의 숫자 2가 있습니다.

예

이것들은 δ(1)와 S(1), δ(2)와 S(2), δ(3)와 S(4)를 생성하는 튜링 기계의 규칙 표이며, δ(5)와 S(5)와 S(6)의 가장 잘 알려진 하한을 나타낸다.다른 시각화의 경우,

표에서 열은 현재 상태를 나타내고 행은 테이프에서 읽은 현재 기호를 나타냅니다.각 테이블 엔트리는 테이프에 쓸 기호, 이동 방향 및 새로운 상태(순서대로)를 나타내는 3글자의 문자열입니다.정지 상태는 H로 표시됩니다.

각 시스템은 상태 A에서 모든 0이 포함된 무한 테이프로 시작합니다.따라서 테이프에서 읽은 첫 번째 기호는 0입니다.

결과 키: (줄 그어진 위치에서 시작, 줄 그어진 위치에서 중단)

1스테이트, 2스테이트의 비버

	A
0	1 RH
1	(미사용)

결과: 0 0 0 0 (1단계, 합계 1단계)

2스테이트, 2스테이트 비버

	A	B
0	1 RB	1LA
1	1파운드	1 RH

결과: 0 0 1 1 1 0 (6단계, 합계 4단계)

3스테이트, 2스테이트의^[19] 비버

	A	B	C
0	1 RB	0RC	1LC
1	1 RH	1 RB	1LA

결과: 0 0 1 1 1 1 1 0 (14단계, 합계 6단계)

이전 기계와 달리, 이것은 오직 δ에 대해서만 사용 중인 비버이며, S에 대해서는 사용되지 않습니다(S(3) = 21).

4스테이트, 2스테이트의 비버

	A	B	C	D
0	1 RB	1LA	1 RH	첫 번째
1	1파운드	0LC	1LD	0RA

결과: 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 (107 스텝, 합계 13 '1')

현재의 5스테이트, 2스테이트의 베스트컨텐더(비버)

	A	B	C	D	E
0	1 RB	1RC	첫 번째	1LA	1 RH
1	1LC	1 RB	0LE	1LD	0LA

결과: 4,7176,870개의 스텝에 8191개의 "0"이 삽입된 4098개의 "1"이 있습니다.

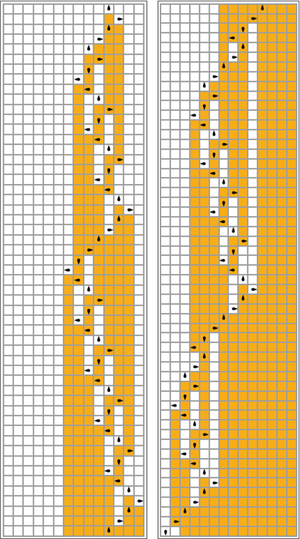
오른쪽 그림에서 이 솔루션이 일부 셀룰러 오토마타의 진화와 질적으로 어떻게 유사한지 확인하십시오.

현재 6스테이트, 2스테이트의 최적 후보

	A	B	C	D	E	F
0	1 RB	1RC	1LD	1 RE	1LA	1LH
1	1LE	1 RF	0RB	0LC	0번째	1RC

결과: §7.412 × 10단계에서 §3.515 × 10^1826736534 "1"s.

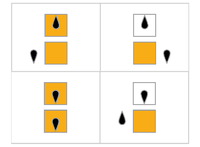
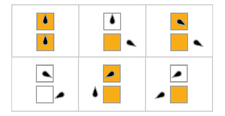
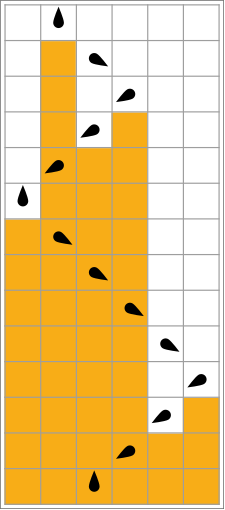
시각화

다음 표에서는 비지 비버별 규칙(δ 최대화)을 시각적으로 나타내며 테이프 상의 "1"에 대응하는 주황색 정사각형과 "0"에 대응하는 흰색으로 나타낸다.머리 위치는 검은색 난형으로 표시되며, 머리 방향은 상태를 나타냅니다.개별 테이프는 수평으로 배치되며 시간은 수직 방향으로 진행됩니다.정지 상태는 1개의 상태를 자신에게 매핑하는 규칙으로 나타납니다(헤드는 이동하지 않습니다).

「 」를 참조해 주세요.

• 라요수
• 터마이트

메모들

레퍼런스

외부 링크

• 위르겐 분트록과 함께 5, 6-상태 튜링 기계에 대한 위의 기록을 발견한 하이너 마르크센의 페이지.
• 파스칼 미쉘의 바쁜 비버 결과에 대한 역사적 조사 또한 최고의 결과와 몇 가지 분석을 포함합니다.
• RTM 클래스의 정의 - Turing Machines, 단순하고 강력한 TM의 하위 클래스입니다.
• 렌셀라 연구소의 바쁜 비버 문제에 관한 밀레니엄 어택.이러한 노력을 통해 몇 가지 새로운 기록을 찾아냈고 4중 공식화를 위한 몇 가지 값을 설정했다.
• Daniel Briggs의 웹 사이트 아카이브 및 포럼은 Baskelete(Georgi Georgiev)의 비정기 기계 목록을 기반으로 5-상태, 2-심볼의 바쁜 비버 문제를 해결합니다.
• Ligocki, Shawn (2021-07-17). "Collatz-like behavior of Busy Beavers". sligocki. Retrieved 2022-07-12.
• 애런슨, 스콧(1999년), 누가 가장 많은 숫자를 말할 수 있을까?
• Weisstein, Eric W. "Busy Beaver". MathWorld.
• 바쁜 비버 튜링 기계 - 컴퓨터 파일
• 파스칼 미셸바쁜 비버 대회: 역사적인 조사.70페이지.2017. <hal-00396880v5>