이진식 트리

이진식 트리는 식을 표현하는 데 사용되는 이진 트리의 특정 종류입니다.이진식 트리가 나타낼 수 있는 두 가지 일반적인 유형의 표현식은 대수식과 부울식입니다^[1].이러한 트리는 단항 ^[1]연산자와 이진 연산자를 모두 포함하는 식을 나타낼 수 있습니다.

다른 바이너리 트리와 마찬가지로 바이너리 식 트리의 각 노드에는 0, 1 또는 2개의 자녀가 있습니다.이 제한된 구조는 식 트리의 처리를 단순화합니다.

개요

식 (a+b)*c+7의 식 트리

이진식 트리의 잎은 상수 또는 변수 이름과 같은 피연산자이며, 다른 노드에는 연산자가 포함됩니다.이러한 특정 트리는 바이너리입니다.모든 연산이 바이너리이기 때문입니다.이것은 가장 간단한 경우이지만 노드에는 2개 이상의 자식이 있을 수 있습니다.단항 마이너스 연산자의 경우와 같이 노드에는 하위 연산자가 하나만 있을 수도 있습니다.왼쪽 및 오른쪽 서브트리를 ^[2]재귀적으로 평가하여 얻은 값에 루트의 연산자를 적용함으로써 표현 트리 T를 평가할 수 있다.

트래버설

괄호화된 왼쪽 식을 재귀적으로 생성하고, 그 후 연산자를 루트로 인쇄하여 마지막으로 괄호화된 오른쪽 식을 재귀적으로 생성함으로써 2진수 표현 트리에서 대수식을 생성할 수 있다.이 일반적인 전략(왼쪽, 노드, 오른쪽)은 순서대로 트래버설이라고 불립니다.대체 통과 전략은 왼쪽 하위 트리, 오른쪽 하위 트리, 그리고 연산자를 재귀적으로 인쇄하는 것입니다.이 트래버설전략은 일반적으로 포스트오더 트래버설이라고 불립니다.세 번째 전략은 연산자를 먼저 인쇄한 후 사전 순서 트래버설로 ^[2]알려진 왼쪽 및 오른쪽 하위 트리를 반복적으로 인쇄하는 것입니다.

이들 3가지 표준 깊이 우선 트래버설은 infix, postfix 및 prefix의 3가지 표현 형식을 나타냅니다.infix 표현은 순서 트래버설로 생성되며, 포스트픽스 표현은 순서 트래버설로 생성되며, 프리픽스 표현은 사전 순서 트래버설로 ^[3]생성된다.

인픽스 트래버설

infix 식을 인쇄할 때는 각 식의 시작과 끝에 개폐 괄호를 추가해야 합니다.각 서브트리가 서브식을 나타내므로 시작 부분에 여는 괄호가 인쇄되고 모든 하위 트리가 처리된 후 닫는 괄호가 인쇄됩니다.

유사 코드:

알고리즘. 혼재하다 (트리) /*식 트리의 infix 식을 인쇄합니다. Pre : 트리는 식 트리에 대한 포인터입니다. 투고: infix 표현이 인쇄되었습니다*/  한다면 (트리 것은 아니다. 빈)     한다면 (트리 상품권 이 교환입니다.)        인쇄물 (열다. 괄호)     끝. 한다면     혼재하다 (트리 왼쪽 서브트리)     인쇄물 (트리 상품권)     혼재하다 (트리 맞다 서브트리)     한다면 (트리 상품권 이 교환입니다.)        인쇄물 (가까운. 괄호)     끝. 한다면  끝. 한다면 끝. 혼재하다 

포스트픽스 트래버설

포스트픽스 표현식은 바이너리 트리의 기본 포스트오더 트래버스에 의해 형성됩니다.괄호는 필요 없습니다.

유사 코드:

알고리즘. 포스트픽스 (트리) /*식 트리의 포스트픽스식을 인쇄합니다. Pre : 트리는 식 트리에 대한 포인터입니다. 투고: 포스트픽스 표현이 인쇄되었습니다*/  한다면 (트리 것은 아니다. 빈)     포스트픽스 (트리 왼쪽 서브트리)     포스트픽스 (트리 맞다 서브트리)     인쇄물 (트리 상품권)  끝. 한다면 끝. 포스트픽스 

프리픽스 트래버설

유사 코드:

알고리즘. 접두사 (트리) /*식 트리의 접두사 식을 인쇄합니다. Pre : 트리는 식 트리에 대한 포인터입니다. 투고: 프리픽스 표현이 인쇄되었습니다*/  한다면 (트리 것은 아니다. 빈)     인쇄물 (트리 상품권)     접두사 (트리 왼쪽 서브트리)     접두사 (트리 맞다 서브트리)  끝. 한다면 끝. 접두사 

식 트리의 구축

트리의 구성은 포스트픽스 식을 한 번에 1개씩 읽음으로써 이루어집니다.기호가 오퍼랜드일 경우 1노드 트리가 생성되고 포인터가 스택에 푸시됩니다.심볼이 연산자일 경우 2개의 트리 T1과 T2에 대한 포인터가 스택에서 팝업되고 루트가 연산자이고 왼쪽과 오른쪽의 자녀가 각각 T2와 T1을 가리키는 새로운 트리가 형성됩니다.그 후 이 새로운 트리에 대한 포인터가 ^[4]스택에 푸시됩니다.

예

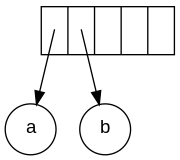
포스트픽스 표기에서의 입력은 다음과 같습니다.a + c d e + * * 처음 2개의 심볼은 오퍼랜드이므로 1노드 트리가 생성되어 포인터가 스택에 푸시됩니다.편의상 스택은 왼쪽에서 오른쪽으로 확장됩니다.

스택이 왼쪽에서 오른쪽으로 확장

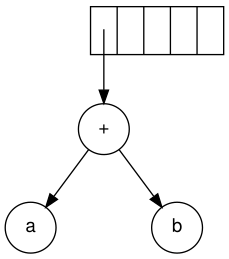
다음 기호는 '+'입니다.그러면 트리에 대한 두 포인터가 팝업되고 새로운 트리가 형성되며 포인터가 스택에 푸시됩니다.

새로운 나무의 형성

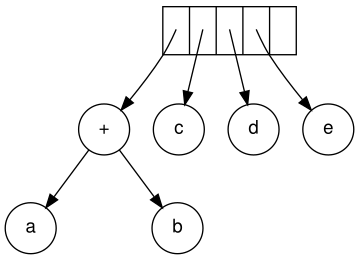
다음으로 c, d, e를 읽습니다.각각에 대해 1노드 트리가 생성되고 대응하는 트리에 대한 포인터가 스택에 푸시된다.

단일 노드 트리 만들기

이어서 '+'가 읽혀지고 마지막 두 트리가 병합됩니다.

두 트리의 결합

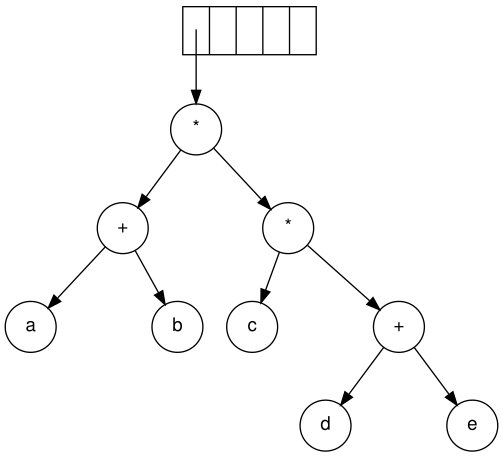
이제 '*'가 읽힙니다.마지막 2개의 트리 포인터가 팝되고 루트로 '*'를 사용하여 새로운 트리가 형성됩니다.

뿌리로 새 나무를 만들다

마지막으로 마지막 심볼을 읽습니다.두 트리가 병합되고 마지막 트리에 대한 포인터가 ^[5]스택에 남아 있습니다.

식 트리 a b + c d e + * 를 작성하는 순서

대수식

((5 + z) / -8) * (4 ^ 2)에 상당하는 이진 대수식 트리

대수식 트리는 숫자, 변수 및 단항 연산자와 이진 연산자를 포함하는 식을 나타냅니다.공통 연산자 중 일부는 ×(곱셈), θ(나눗셈), +(더하기), -(감산), ^(표현), -(부정)이다.연산자는 트리의 내부 노드에 포함되어 리프 노드의 ^[1]수와 변수가 포함됩니다.이진 연산자의 노드에는 2개의 하위 노드가 있으며, 단항 연산자에는 1개의 하위 노드가 있습니다.

부울식

(true$$express\$displaystyle \lor }$ false$$ $\wedge {\displaystyle }${ $displaystyle \land$}$$${\displaystyle \mathrm{}}$${\$ { $displaystyle \neg$$$} false ) ) { $displaystyle \lor$}$$ (true${\\displaystyle \lor$$$} false)에 상당하는 바이너리 부울식 트리

부울식은 대수식과 매우 유사하게 표현되며, 유일한 차이점은 사용된 특정 값과 연산자입니다.부울식에서는 true 및 false를 상수값으로 사용하며 연산자에는 $"\displaystyle \land"($AND), $"\displaystyle \lor"($OR), $"\displaystyle \neg"($NOT)가 있습니다.

「 」를 참조해 주세요.

• 식(수학)
• 용어(논리)
• 문맥 자유 문법
• 해석 트리
• 추상 구문 트리

레퍼런스