쌍선형 보간법

z 값이 0, 1, 1 및 0.5인 단위 사각형의 쌍선형 보간 예제입니다.색상으로 표시되는 중간 보간 값입니다.

수학에서 쌍선형 보간은 반복 선형 보간을 사용하여 두 변수(예: x와 y)의 함수를 보간하는 방법이다.임의 볼록 4변수(메쉬)의 정점에 정의된 함수에 일반화될 수 있지만, 일반적으로 2D 직선 그리드에서 샘플링된 함수에 적용된다.

쌍선형 보간은 먼저 한 방향으로 선형 보간한 후 다른 방향으로 다시 선형 보간을 사용하여 수행됩니다.표본 추출된 값과 위치에서는 각 단계가 선형이지만, 전체 보간은 선형적이 아니라 표본 위치에서는 2차적입니다.

쌍선형 보간은 컴퓨터 비전 및 이미지 처리의 기본 재샘플링 기술 중 하나로, 쌍선형 필터링 또는 쌍선형 텍스처 매핑이라고도 합니다.

계산

빨간색 점 4개는 데이터 점을 나타내고 녹색 점은 보간할 지점을 나타냅니다.

점(x, y)에서 알 수 없는 함수 f의 값을 찾으려고 합니다.4개의 점 Q₁ = (x₁₁₂, y), Q₁ = (x₂₂₁, y), Q₂ = (x₁, y), Q = (x₂, y₁₁)에서₂₂₂ f의 값을 알고 있다고 가정합니다.

반복 선형 보간

먼저 x방향으로 선형 보간법을 시행합니다.이것은 산출된다.

({displaystyle {x,y_{1})f(x,y_{1})=black {x_{2}-x_{1}f(Q_{11})+{\frac {x_{2}-x_{1}}f(Q_{21}),\f(x_{2})\end { aligned}}

원하는 추정치를 얻기 위해 y 방향으로 보간하여 진행합니다.

{\displaystyle{\begin{정렬}(x, y)&, ={\frac{{2y_}-y}{y_{2}-y_{1}}}f(x,y_{1})+{\frac{y-y_{1}}{y_{2}-y_{1}}}f(x,y_{2})\\&, ={\frac{{2y_}-y}{y_{2}-y_{1}}}\left({\frac{x_{2}-x}{x_{2}-x_{1}}}f(Q_{11})+{\frac{x-x_{1}}{x_{2}-x_{1}}}f(Q_{21})\right)+{\frac{y-y_{1}}{y_{2}-y_{1}}}\left({\frac{x_{2}-x}{x_{2}-x_{1}}}f(Q_{12})+{\frac{x-x_{1}}{x_.{2}-x_{1}}f(Q_{22}\오른쪽)\\&=sqfrac {1}{(x_{2}-x_{1})(y_{2}-y_{1})}}}\left(x_{11})(x_{2}-x)(y_{2}-y)+f(Q_{21)(x-x_{1})(y_12)\&=beginfrac {1}{(x_{2}-x_{1})(y_{2}-y_{1})}}{\begin{bmatrix}x_{2}-x&x_{1}\end{bmatrix}f(Q_{11})&f(Q_12)\end { aligned}}

먼저 Y 방향을 따라 보간 작업을 수행한 후 ^[1]x 방향을 따라 보간 작업을 수행해도 동일한 결과에 도달합니다.

다항식 적합도

다른 방법은 보간 문제에 대한 해답을 다선형 다항식으로 쓰는 것이다.

f(x,y)\about a_{00}+a_{10}xy+a_{01}y+a_{11}xy,

여기서 계수는 선형 시스템을 풀어서 찾을 수 있다.

}}정렬}

결과를 낳다

{\displaystyle{\begin{정렬}{\begin{bmatrix}a_{00}\\a_{10}\\a_{01}\\a_{11}\end{bmatrix}}={\frac{1}{ᆨ ᆩ}}{\begin{bmatrix}x_{2}y_{2}&, -x_{2}y_{1}&, -x_{1}y_{2}&, x_{1}y_{1}\\-y_{2}&, y_{1}&, y_{2}&, -y_{1}\\-x_{2}&, x_{2}&, x_{1}&, -x_{1}\\1&, -1&, -1&, 1\end{bmatrix}}{\begin{bmatrix}(Q_{11})\\f(Q_{12})\\f(Q_{21})\\f(Q_{22})\end{bmatrix}}.\end { aligned}}

가중평균

쌍선형 보간법의 기하학적 시각화입니다.원하는 지점(검은색)과 전체 면적의 곱은 각 모서리의 값과 대각선의 반대쪽 부분 면적의 곱(해당 색상)의 합과 같다.

해는 f(Q)의 가중 평균으로도 쓸 수 있다.

({displaystyle f(x,y)\about w_{11}f(Q_{11})+w_{12}f(Q_{12})+w_{214}f(Q_{22})+w_{22}f(Q_{22})},

여기서 가중치는 1로 합하고 전치된 선형 시스템을 만족시킨다.

{\displaystyle {bmatrix}1&1\x_{1}&x_{1}&x_{1}&x_{1}&y_{1}&y_{1}&y_{1}&y_{1}&x_1}&x_{1}&x_1}&x_1}&x_1}&x_1}&x_1}&x_1}&x_1}&x_1}&x_1}&x_1}&x_1}&1}&x_1}&_1}&x_1}&_1}''''''''''''''''''''''

결과를 낳다

{\displaystyle{\begin{정렬}{\begin{bmatrix}w_{11}\\w_{21}\\w_{12}\\w_{22}\end{bmatrix}}={\frac{1}{(x_{2}-x_{1})(y_{2}-y_{1})}}{\begin{bmatrix}x_{2}y_{2}&, -y_{2}&, -x_{2}&, 1\\-x_{2}y_{1}&, y_{1}&, x_{2}&, -1\\-x_{1}y_{2}&, y_{2}&, x_{1}&, -1\\x_{1}y_{1}&, -y_{1}&, -x_{1}&, 1\end{bmatrix}}{\begin{bmatrix}1\\x\\y\\xy\end{bmatrix}},\end{정렬}}}

그 결과,

{\displaystyle {signed}w_{11}&=(x_{2}-x)(y_{2}-x_{1})(y_{2}-y_{1}),\w_{12}&=(x_{2}-x)(y_{1})

반복 선형 보간법으로 얻은 결과와 일치한다.가중치 집합은 직사각형의 일반화 중심 좌표 집합으로도 해석할 수 있다.

대체 행렬 형식

위의 내용을 조합하여

{\displaystyle{\begin{정렬}(x, y)\approx{\frac{1}{(x_{2}-x_{1})(y_{2}-y_{1})}}{\begin{bmatrix}(Q_{11})&, f(Q_{12})&, f(Q_{21})&, f(Q_{22})\end{bmatrix}}{\begin{bmatrix}x_{2}y_{2}&, -y_{2}&, -x_{2}&, 1\\-x_{2}y_{1}&, y_{1}&, x_{2}&, -1\\-x_{1}y_{2}&, y_{2}&, x_{1}&, -1\\x_{1}y_{1}&, -y_{1}&, -x_{1}&, 1\end{bmatrix}}{\begin{bmatrix}1\\x\\y\\xy\end{bmatrix}}.\end { aligned}}

유닛 스퀘어

f가 알려진 4개의 점이 (0, 0), (1, 0), (0, 1), (1, 1)인 좌표계를 선택하면 보간 공식은 다음과 같이 단순화됩니다.

f(x,y)\approx f(0,0)(1-y)+f(1,0)+f(0,1)y(1,1)xy,

또는 이와 동등하게 행렬 연산:

f(x,y)\약 {\display{bmatrix}1-x&x\end{bmatrix}{\display{bmatrix}f(0,0)&f(1,1)\end{bmatrix}{\display{bmatrix}1-y\matrix}{\displaysty}

여기에서는 중량도 인식합니다.

{signed}w_{11}&=(1-y),\w_{12}&=(1-x)y,\w_{21)&=xy,\w_{22}&=xy.\end { aligned}

또는 단위 정사각형상의 보간물은 다음과 같이 쓸 수 있다.

f(x,y)=a_{00}+a_{10}x+a_{01}y+a_{11}xy,

어디에

{displaystyle}a_{00}&=f(0,0),\a_{01)-f(0,0),\a_{011}&=f(1,1)-f(0,0)-0,+f(0,0)\end { aligned}

두 경우 모두 상수(4개)의 수는 f가 주어진 데이터 점의 수에 해당합니다.

특성.

일부 1차원 및 2차원 보간과 2차원 보간 비교.
검은색과 빨간색/노란색/녹색/파란색 점은 각각 보간된 점 및 인접 표본에 해당합니다.
그들의 지상 높이는 그들의 가치와 일치한다.

이름에서 알 수 있듯이, 쌍선형 보간은 선형은 아니지만 x 또는 y 방향에 평행한 선을 따라 선형(즉, 아핀)이며, x 또는 y가 일정하게 유지되면 동등하게 됩니다.다른 직선을 따라 보간법은 2차입니다.보간은 위치(x 및 y)에서 선형은 아니지만, 위의 (행렬) 방정식에서 볼 수 있듯이 고정점에서는 보간 값에서 선형입니다.

쌍선형 보간 결과는 어느 축이 먼저 보간되고 어느 축이 두 번째 보간되는지와는 무관합니다.처음에 y방향과 x방향으로 선형 보간을 수행했다면 결과 근사치는 동일했을 것이다.

보간은 이중선형 다항식이며, 라플라스 방정식을 만족시키는 조화 함수이기도 합니다.그래프는 쌍선형 베지어 표면 패치입니다.

역과 일반화

일반적으로 보간은 무한한 수의 점(하이포볼라의^[2] 가지를 형성하는 것)에서 (정점 값의 볼록한 선체에 있는) 값을 가정하기 때문에 보간은 반전되지 않습니다.

그러나 벡터 필드를 보간하는 경우와 같이 두 기능에 동시에 쌍선형 보간을 적용하면 보간은 (특정 조건에서) 반전할 수 있습니다.특히, 이 역수를 사용하여 볼록한 사각형 안에 있는 점의 "단위 제곱 좌표"를 찾을 수 있습니다(단위 제곱에 2진 보간된 벡터 장으로서 사각형 좌표를 고려함).병렬 사변형이 아닌 경우 계산이 ^[3]훨씬 복잡하지만 이 절차를 사용하여 볼록 사변형으로 확장할 수 있습니다.사변형 사이의 결과 맵은 쌍선형 변환, 쌍선형 왜곡 또는 쌍선형 왜곡으로 알려져 있습니다.

또는 사각형과 단위 정사각형 사이의 투영 매핑을 사용할 수 있지만, 결과적으로 발생하는 보간물은 이중선이 되지 않는다.

사변형이 평행사변형인 특별한 경우 단위사각형에 대한 선형 매핑이 존재하며 일반화가 쉽게 이루어진다.

쌍선형 보간법을 3차원으로 확대한 것을 삼선형 보간이라고 한다.

역계산

F $(\textstyle$ F)를 ${\textstyle F}$ ${\textstyle \mu ,\lambda \in [0,1]}$ μ , ${\textstyle \mu ,\lambda \in [0,1]}$ [ ${\textstyle \mu ,\lambda \in [0,1]}$ , 1 ${\textstyle \mu ,\lambda \in [0,1]}$ ] , $\textstyle$ \mu , $\lambda \in [$ 0 , 1 ${\textstyle \mu ,\lambda \in [0,1]}$ 로 ${\textstyle \mu ,\lambda \in [0,1]}$ 된 단위 정사각형에 대해 초기 보간되는 벡터 ${\textstyle F}$ 라고 가정합니다. 보간을 반전시키려면 다음 두 개의 2선형 다항식 시스템을 풀어야 합니다.

A+B\lambda +C\mu +D\lambda \mu = 0

어디에

디스플레이 스타일A&=F_{00}-F\B&=F_{10}-F_{00}\\C&=F_{01}-F_{00}\D&=F_{11}-F_{01}-F_{10}+F_{00}\end{aligned}}

신중하게 선택된 벡터를 사용하여 시스템의 2-d 교차 곱(그래스맨 제품 참조)을 취하면 다음과 같은 용어를 제거할 수 있습니다.

(\displaystyle(A+B\lambda +C\mu)&\times D&=0\(A+B\lambda)&\times (C+C\mu)&\times (B+D\mu)=0\times (B+D\lambda)&\times (A+D\lambda)&\lambda}

로 확장됩니다.

{displaystyle} c+e\b+(c+d)\displayda +e\displayda ^{2}&=0\a+(c-d)\mu +f\mu ^{2}&=0\end{aligned}

어디에

{\displaystyle\narged}a&=A\times B\b&=A\times C\qquad d=B\times C\c&=A\times D\qquad e=B\times D\qquad f=C\times D\end {aligned}}

2차 방정식은 2차 공식을 사용하여 풀 수 있습니다.우리는 동등한 결정 인자를 가지고 있다.

\mathbb {D} =(c+d)^{2}-4eb=(c-d)^{2}-4fa

및 솔루션

{\displaystyle\c-d\pm {-c-d}{2e}\qquad \mu =\displayfrac {-c+d\mp}{2f}}

(직선관계에 의해 부호가 강제됩니다).e

e=0

e=0

{

displaystyle

e

=0}

f=0

f

f=0

{

displaystyle

f

=0}

인

f=0

e=0

는 별도로 처리해야 합니다.적절한 조건이 주어진 경우 두 솔루션 중 하나가 장치 정사각형에 있어야 합니다.

이미지 처리에서의 응용 프로그램

컴퓨터 비전과 화상 처리에서는, 쌍선형 보간법을 사용해 화상이나 텍스처를 재샘플링 합니다.알고리즘은 텍스처 맵 상의 대응하는 점에 스크린 픽셀 위치를 매핑하기 위해 사용된다.4개의 주변 텍셀 속성의 가중평균(색, 투명도 등)을 산출해 스크린 픽셀에 적용한다.이 과정은 ^[4]텍스처 처리 대상 객체를 형성하는 각 픽셀에 대해 반복됩니다.

영상의 크기를 조정해야 하는 경우, 원래 영상의 각 픽셀은 스케일 상수에 따라 특정 방향으로 이동해야 합니다.그러나 비적분 스케일 팩터로 이미지를 스케일업할 경우 적절한 픽셀 값이 할당되지 않은 픽셀(즉, 구멍)이 있습니다.이 경우 출력 이미지에 값이 없는 픽셀이 없도록 이러한 구멍에 적절한 RGB 또는 그레이스케일 값을 할당해야 합니다.

픽셀 매칭에 의한 완벽한 영상 변환이 불가능한 경우 쌍선형 보간법을 사용하면 픽셀에 적절한 강도 값을 계산하여 할당할 수 있습니다.가장 가까운 이웃의 보간법이나 2차 보간법과 같은 다른 보간법과는 달리, 쌍선형 보간법은 해당 픽셀의 적절한 색상 강도 값을 찾기 위해 주어진 픽셀에서 대각선 방향으로 위치한 가장 가까운 4개의 픽셀 값만 사용합니다.

쌍선형 보간은 미지의 픽셀의 계산된 위치를 둘러싼 알려진 픽셀 값의 가장 가까운 2 × 2 근방을 고려한다.그런 다음 이 4픽셀의 가중 평균이 최종 보간 ^[5]^[6]값에 도달합니다.

그레이스케일 값의 쌍선형 보간 예제

예

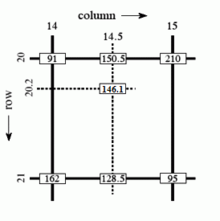
오른쪽 예에서 보듯이, 20.2행, 14.5열에 있는 픽셀의 강도 값은 각 행 20과 21의 열 14와 15의 값 사이에 먼저 선형 보간하여 계산할 수 있습니다.

디스플레이 스타일I_{20,14.5} & = frac {15-14}5}{15-14}\cdot 91+{\frac {14.5-14}{15-14}\cdot 210=150.5,\I_{21,14}.5} & = frac {15-14}5}{15-14}\cdot 162+{\frac {14.5-14}{15-14}\cdot 95=128.5,\end {aligned}}

그리고 이 값들 사이에 선형으로 보간해서

I_{20.2,14.5}=124 frac {21-20}.2){21-20}\cdot 150.5+{\frac {20.2-20}{21-20}\cdot 128.5=162.1.

이 알고리즘은 이미지 크기를 비통합 줌 배율로 조정함으로써 발생하는 시각적 왜곡을 줄여주며, 일부 픽셀은 크기 조정된 이미지에서 다른 픽셀보다 크게 표시됩니다.

「」를 참조해 주세요.

레퍼런스

^ Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (1992). Numerical recipes in C: the art of scientific computing (2nd ed.). New York, NY, USA: Cambridge University Press. pp. 123-128. ISBN 0-521-43108-5.
^ Monasse, Pascal (2019-08-10). "Extraction of the Level Lines of a Bilinear Image". Image Processing On Line. 9: 205–219. doi:10.5201/ipol.2019.269. ISSN 2105-1232.
^ Quilez, Inigo (2010). "Inverse bilinear interpolation". iquilezles.org. Archived from the original on 2010-08-13. Retrieved 2021-07-28.
^ 쌍선형 보간 정의(www.pcmag.com에서 인기 있는 기사).
^ Khosravi, M. R. (2021-03-19). "BL-ALM: A Blind Scalable Edge-Guided Reconstruction Filter for Smart Environmental Monitoring Through Green IoMT-UAV Networks". IEEE Transactions on Green Communications and Networking. 5: 727–736. doi:10.1109/TGCN.2021.3067555.
^ "웹 튜토리얼: 디지털 이미지 보간"을 참조하십시오.

[1] Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (1992). Numerical recipes in C: the art of scientific computing (2nd ed.). New York, NY, USA: Cambridge University Press. pp. 123-128. ISBN 0-521-43108-5.

[2] Monasse, Pascal (2019-08-10). "Extraction of the Level Lines of a Bilinear Image". Image Processing On Line. 9: 205–219. doi:10.5201/ipol.2019.269. ISSN 2105-1232.

[3] Quilez, Inigo (2010). "Inverse bilinear interpolation". iquilezles.org. Archived from the original on 2010-08-13. Retrieved 2021-07-28.

[4] 쌍선형 보간 정의(www.pcmag.com에서 인기 있는 기사).

[5] Khosravi, M. R. (2021-03-19). "BL-ALM: A Blind Scalable Edge-Guided Reconstruction Filter for Smart Environmental Monitoring Through Green IoMT-UAV Networks". IEEE Transactions on Green Communications and Networking. 5: 727–736. doi:10.1109/TGCN.2021.3067555.

[6] "웹 튜토리얼: 디지털 이미지 보간"을 참조하십시오.

[1]

[2]

[3]

[4]

[5]

[6]

Search

쌍선형 보간법

네임스페이스

더

목차

계산

반복 선형 보간

다항식 적합도

가중평균

대체 행렬 형식

유닛 스퀘어

특성.

역과 일반화

이미지 처리에서의 응용 프로그램

예

「」를 참조해 주세요.

레퍼런스

Search

쌍선형 보간법

계산

반복 선형 보간

다항식 적합도

가중평균

대체 행렬 형식

유닛 스퀘어

특성.

역과 일반화

이미지 처리에서의 응용 프로그램

예

「 」를 참조해 주세요.

레퍼런스

「」를 참조해 주세요.