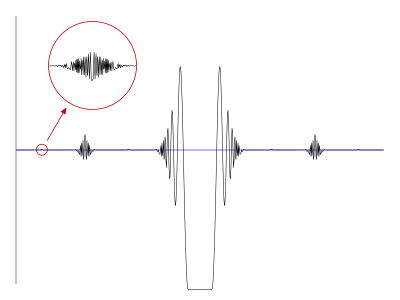
볼테라 함수

이 글에는 출처가 없다 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Volterra의 기능" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2021년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

수학에서 Vito Volterra의 이름을 딴 Volterra의 함수는 실선 R에 정의된 실제 값 함수 V로 다음과 같은 기이한 속성 조합을 가지고 있다.

• V는 어디서나 차별화된다.
• 파생상품 V ′은 어디에나 한정되어 있다.
• 그 파생상품은 Riemann-integrated가 아니다.

정의 및 시공

The function is defined by making use of the Smith–Volterra–Cantor set and "copies" of the function defined by ${\displaystyle f(x)=x^{2}\sin(1/x)}$ for ${\displaystyle x\neq 0}$ and ${\displaystyle f(0)=0}$. The construction of V begins by determining the largest value of x in f ′(x) = 0인 간격 [0, 1/8]. 일단 이 값(say₀ x)이 결정되면, f₀(x)의 상수값을 사용하여 오른쪽으로 기능을 1/8 지점까지 확장한다.이 작업이 완료되면 1/4 지점에서 시작하여 0 방향으로 아래로 확장되는 기능의 미러 이미지를 생성할 수 있다.이 함수는 [0, 1/4] 구간을 벗어나 0으로 정의된다.그런 다음 이 함수를 구간[3/8, 5/8]으로 변환하여 결과 함수는, 우리가 f라고₁ 부르는, Smith-Volterra-Canter 집합의 보완 중간 구간에서만 0이 되도록 한다.f를₂ 구성하기 위해 f ′은 더 작은 간격[0,1/32]에 대해 고려한다. 마지막으로 파생상품이 이전과 같은 방식으로 0, 확장, 미러링되고, 결과함수의 번역된 복사본 2개를₁ f에 추가하여₂ f함수를 생산한다.그러면 볼테라의 기능은 스미스-볼터라-칸토어 집합의 구성에서 제거된 모든 간격에 대해 이 절차를 반복함으로써 결과를 얻는다. 즉, 함수 V는 함수 f₁, f₂, ...의 시퀀스 제한이다.

추가 특성

볼테라의 기능은 f(위에서 정의한 바와 같이)가 그렇듯이 어디에서나 다를 수 있다.f ′(x) = 2x sin(1/x) - cos(1/x) x ≠ 0을 나타낼 수 있는데, 이는 0의 근처에서는 f ′이 값 1과 -1을 취하는 점이 있다는 것을 의미한다.따라서 Smith-Volterra-Cantor 세트 S의 구성에서 제거된 간격의 각 끝점의 모든 이웃에서 V ′이 값 1과 -1을 취하는 지점이 있다.사실 V ′은 S의 모든 점에서 V자체가 다르지만 파생상품 0으로 S의 모든 점에서 불연속적이다.단, V ′은 S의 시공에서 제거된 간격마다 연속적이므로 V ′의 불연속 세트는 S와 동일하다.

Smith-Volterra-Cantor set S는 양의 Lebesgue 측정치를 가지고 있으므로, 이는 V ′이 일련의 양의 측정치에 불연속적이라는 것을 의미한다.리만 통합성에 대한 르베그의 기준에 따르면, V ′은 리만 통합이 가능하지 않다.만약 어떤 사람이 "지방" (긍정적 측정) 칸토어 설정 S 대신에 일반적인 측정치-0 칸토어 설정 C로 볼테라의 함수 구성을 반복한다면, 어떤 사람은 유사한 특성을 가진 많은 함수를 얻게 되지만, 파생상품은 양성 측정 집합 S 대신에 측정치 설정 C에서 불연속될 것이고, 따라서 결과적으로 재미를 얻게 될 것이다.리만 통합형 파생상품이 있을 것이다.

참고 항목

• 미적분학의 기본 정리

외부 링크

• 미적분학의 기본 정리와의 씨름: 볼테라의 기능, 데이비드 마리우스 브레수드의 대화
• PPT(통합할 수 없는 파생상품)에 대한 Volterra의 예시, 데이비드 마리우스 브레수드(David Marius Breshoud