슈퍼퍼뮤테이션

Superpermutation
3개의 기호 슈퍼퍼머튜션에서 순열의 분포.

조합수학에서 n 기호에 대한 초퍼머뮤테이션(superpermutation)은 n 기호의 각 순열을 하위 문자열로 포함하는 문자열이다.사소한 슈퍼퍼튜팅은 단순히 함께 나열되는 순열로 구성될 수 있는 반면, 오버랩이 허용되기 때문에 (n = 1)의 사소한 경우를 제외하고) 슈퍼퍼튜팅도 더 짧아질 수 있다.예를 들어, n = 2의 경우, 초퍼뮤테이션 1221은 가능한 모든 순열(12과 21)을 포함하지만, 짧은 문자열 121은 순열도 모두 포함한다.

1㎛ n ≤ 5의 경우, n 기호에 대한 최소 초점화 길이가 1! + 2! + … + n!(OEIS에서 연속 A180632)인 것으로 나타났다.처음 네 개의 가장 작은 초점수는 각각 길이 1, 3, 9, 33을 가지며 문자열 1, 121, 121, 123121321 및 123412142312431242132413214321을 형성한다.단, n = 5의 경우 길이가 153인 최소 수퍼퍼머가 몇 개 있다.아래에는 그러한 초퍼머션(superpermutation)이 한 개 나타나 있는 반면, 같은 길이의 다른 하나는 문자열의 후반부에 있는 4와 5를 모두 전환하여 얻을 수 있다([1]볼드 2 이후).

123451234152341253412354123145231425314235142315423124531243512431524312543121345213425134215342135421324513241532413524132541321453214352143251432154321

n > 5의 경우, 아직 최소한의 초점화도 증명되지 않았고, 그들을 찾을 수 있는 패턴도 발견되지 않았지만, 그에 대한 하한과 상한은 발견되었다.

슈퍼퍼뮤테이션 찾기

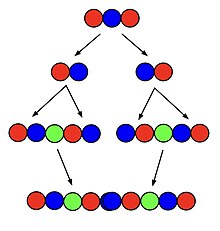
2개의 기호가 있는 슈퍼퍼머튜션에서 3개의 기호가 있는 슈퍼퍼머티션을 생성하는 다이어그램.

순서 의 슈퍼퍼머루션을 생성하기 위한 가장 일반적인 알고리즘 중 하나는 재귀 알고리즘이다.첫째, 순서 - 의 초퍼머레이션(superpermutation) 을 초퍼머션에 나타난 순서대로 개별 순열로 나눈다.그런 다음 각 순열은 두 복사본 사이에 n번째 기호가 추가된 자신의 복사본 옆에 배치된다.마지막으로, 각 결과 구조물은 서로 옆에 배치되고 인접한 모든 동일한 기호가 병합된다.[2]

예를 들어, 순서 3의 초퍼퍼머레이션은 2개의 기호가 있는 하나에서 만들어질 수 있다; 초퍼머퓨테이션 121부터 시작해서 그것을 순열 12와 21로 나누면 순열은 복사되어 12312와 21321로 배치된다.이들을 함께 배치해 1231221321을 만들고, 중간에 동일한 인접 2s를 병합해 123121321을 만들게 되는데, 이는 실로 순서 3의 초퍼퍼레이션이다.이 알고리즘은 n이 5보다 작거나 같은 모든 n에 대해 가능한 최단 시간 초과를 초래하지만, n이 그 이상으로 증가함에 따라 가능한 최단 시간보다 점점 더 길어진다.[2]

초점수를 찾는 또 다른 방법은 각 순열이 정점이고 모든 순열이 가장자리로 연결되는 그래프를 만드는 것이다.각 가장자리는 그것과 관련된 가중치를 가지고 있다; 가중치는 한 순열의 끝에 얼마나 많은 문자를 추가할 수 있는지(처음부터 동일한 수의 문자를 떨어뜨림) 보고 다른 순열의 결과로 이어질 수 있는지를 보고 계산된다.[2]예를 들어, 123 + 12 = 12312 = 312이기 때문에 123 ~ 312 사이의 가장자리의 무게는 2이다.생성된 그래프를 통과하는 해밀턴식 길은 모두 초점이며, 가장 작은 무게로 길을 찾는 문제는 여행하는 세일즈맨 문제의 한 형태가 된다.길이 + 2+ 1은(는) 로빈 휴스턴의 이 방법에 대한 컴퓨터 검색을 사용하여 발견되었다.[3]

하한 및 상한

6개 이상의 기호에 대한 가장 작은 수퍼퍼뮤테이션을 찾기 위한 알고리즘은 아직 해결되지 않았다.그러나 몇 가지 증거가 시간이 흐르면서 문제의 강한 상·하한선을 점차 조여왔다.

하한 또는 하루히 문제

2011년 9월 4찬의 Science & Math("/sci/") 게시판에 붙은 익명의 포스터는 n 기호(n ≥ 2)의 최소 슈퍼퍼뮤테이션이 최소 길이 n! + (n-1) + (n-2)! + n - 3이라는 것을 증명했다.[4]일본의 애니메이션 시리즈 《스즈미야 하루히의 우울》과 관련하여, 이미지판에 문제가 "하루히 문제"로 제시되었다: 만약 당신이 가능한 모든 순서로 시리즈 첫 시즌의 14편을 보고 싶다면, 당신이 봐야 할 가장 짧은 연속 에피소드는 무엇인가?[5]수학자 겸 컴퓨터 과학자 로빈 휴스턴이 트위터를 통해 이 같은 하한선에 대한 증거는 2018년 10월 일반 대중의 관심을 끌었다.[4]2018년 10월 25일, 로빈 휴스턴, 제이 팬톤, 빈스 바터는 온라인 정수기 백과사전(OEIS)에 이 증명의 정제된 버전을 게재했다.[5][6]"Anonymous 4chan 포스터"로 인정된 이 증빙의 출판판은 Engen과 Vatter(2019년)에 나타난다.[7]구체적으로 「하루히 문제」(14개 기호의 경우)의 경우, 하한은 현재 최소 93,884,313,611이고, 상한은 최대 93,924,230,411이다.[4]

상한

2018년 10월 20일, 대칭 집단의 케이리 그래프를 통해 해밀턴 경로를 건설하기 위한 애런 윌리엄스의 공법을 채택함으로써, 그렉 이건은 길이 n! + (n-1)! (n-2)! (n-3)+n - 3의 초단계를 생산할 알고리즘을 고안했다.[8][2]2018년까지, 이것들은 n ≥ 7로 알려진 가장 작은 초특급이었다.그러나 2019년 2월 1일 보그단 코안다는 신기록인 길이 5907의 n=7, 즉 (n!+(n-1)+(n-2)+(n-3)+(n-3)-1의 슈퍼퍼머션을 발견했다고 발표했다.[2]2019년 2월 27일 로빈 휴스턴이 개발한 아이디어를 이용해 이건은 길이 5906의 n = 7에 대한 초퍼머메이션을 제작했다.[2]n > 7의 값에 대해서도 유사한 짧은 수퍼퍼뮤테이션이 존재하는지 여부는 여전히 열려 있는 문제로 남아 있다.n = 7의 현재 최고 하한(위 섹션 참조)은 여전히 5884이다.

참고 항목

추가 읽기

  • Ashlock, Daniel A.; Tillotson, Jenett (1993), "Construction of small superpermutations and minimal injective superstrings", Congressus Numerantium, 93: 91–98, Zbl 0801.05004
  • Anonymous 4chan Poster; Houston, Robin; Pantone, Jay; Vatter, Vince (October 25, 2018). "A lower bound on the length of the shortest superpattern" (PDF). On-Line Encyclopedia of Integer Sequences.

참조

  1. ^ Johnston, Nathaniel (July 28, 2013). "Non-uniqueness of minimal superpermutations". Discrete Mathematics. 313 (14): 1553–1557. arXiv:1303.4150. Bibcode:2013arXiv1303.4150J. doi:10.1016/j.disc.2013.03.024. S2CID 12018639. Zbl 1368.05004. Retrieved March 16, 2014.
  2. ^ a b c d e f Egan, Greg (20 October 2018). "Superpermutations". gregegan.net. Retrieved 15 January 2020.
  3. ^ Houston, Robin (21 August 2014), "Tackling the Minimal Superpermutation Problem", arXiv:1408.5108 [math.CO]
  4. ^ a b c Griggs, Mary Beth. "An anonymous 4chan post could help solve a 25-year-old math mystery". The Verge.
  5. ^ a b Klarreich, Erica (November 5, 2018). "Sci-Fi Writer Greg Egan and Anonymous Math Whiz Advance Permutation Problem". Quanta Magazine. Retrieved June 21, 2020.{{cite web}}: CS1 maint : url-status (링크)
  6. ^ Anonymous 4chan poster; Houston, Robin; Pantone, Jay; Vatter, Vince (October 25, 2018). "A lower bound on the length of the shortest superpattern" (PDF). OEIS. Retrieved 27 October 2018.
  7. ^ Engen, Michael; Vatter, Vincent (2021), "Containing all permutations", American Mathematical Monthly, 128 (1): 4–24, doi:10.1080/00029890.2021.1835384
  8. ^ Aaron, Williams (2013). "Hamiltonicity of the Cayley Digraph on the Symmetric Group Generated by σ = (1 2 ... n) and τ = (1 2)". arXiv:1307.2549v3 [math.CO].

외부 링크