단면계수

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "섹션 계수" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2009년 10월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

단면계수는 보 또는 휨 부재의 설계에 사용되는 주어진 단면에 대한 기하학적 특성이다.설계에 사용된 기타 기하학적 특성에는 장력과 전단 면적의 경우, 압축을 위한 교정의 반지름, 강성을 위한 관성 모멘트 및 극성 모멘트가 포함된다.이들 속성 사이의 어떤 관계도 문제의 모양에 크게 좌우된다.공통 도형의 단면 모듈에 대한 방정식은 다음과 같다.단면모듈리에는 탄성단면모듈루스와 플라스틱단면모듈루스가 있다.다른 프로파일의 섹션 모듈리는 또한 그러한 속성을 나열하는 표에서 공통 프로파일에 대한 숫자 값으로 찾을 수 있다.

표기법

북미 및 영국/호주 협약은 S&Z의 사용을 역행한다.탄성 계수는 북미에서는 ^[1]S이지만 영국/호주에서는 Z,^[2] 플라스틱 계수는 그 반대다.Eurocode 3(EN 1993 - Steel Design)은 두 가지 모두에 대해 W를 사용함으로써 이 문제를 해결하지만 첨자 W와_pl W를_el 사용함으로써 이 둘을 구분한다.

탄성단면계수

일반 설계의 경우 탄성 단면 계수를 사용하여 대부분의 금속 및 기타 공통 재료에 대해 항복점까지 적용한다.

탄성 단면 계수는 S = I / y로 정의되며 여기서 나는 면적의 두 번째 모멘트(또는 관성의 모멘트와의 혼동되지 않는 영역 모멘트)이며 y는 중성축에서 주어진 섬유까지의 거리이다.흔히 y = c를 사용하여 보고되는데, 여기서 c는 아래 표와 같이 중립 축에서 가장 극한 섬유까지의 거리다.또한_y M = S ⋅ σ_y σ, 여기서_y σ은 재료의 항복강도라고 하는 항복모멘트(M_y)를 결정하는 데도 자주 사용된다.

단면 계수 방정식^[3]

단면형	피겨	방정식	댓글
직사각형		${\displaystyle S={\cfrac {bh^{2}}{6}}}$	솔리드 화살표는 중립 축을 나타냄
이중 대칭 I-섹션(주요 축)		${\displaystyle Sx={\cfrac {BH^{2}}-{6}-{\cfrac {bh^{3}}{6}}{6}H}}$ ${\displaystyle S}$ ${\displaystyle x}$= ${\displaystyle I\frac{}{}}$ ${\displaystyle \frac{x}{}}$ ${\displaystyle \frac{}{}}$ ${\$ 포함($y{\displaystyle }$= ${\displaystyle \frac{H}{}}$ ${\displaystyle \frac{2}{}}$ ${\$	NA는 중립 축을 나타낸다.
이중 대칭 I-섹션(최소 축)		${\displaystyle Sy={\cfrac {B^{2}(H-h)}{6}{6}}{6}+{\cfrac {(B-b)^{3}h}{6B}}$[4]	NA는 중립 축을 나타낸다.
원		${\displaystyle S={\cfrac {\pi d^{3}{32}}}$[3]	솔리드 화살표는 중립 축을 나타냄
원형 중공 단면		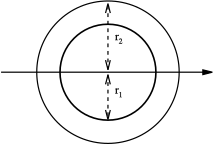${\displaystyle S={\cfrac {\pi \left(r_{2}^{4}-r_{1}^{1}\오른쪽)}{4r_{2}}:{4}={\cfrac {\pi(d_{2}^{4}-d_{1}^}}}}{2}}:}$	솔리드 화살표는 중립 축을 나타냄
직사각형 중공 단면		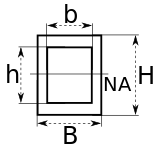${\displaystyle S={\cfrac {BH^{2}}-{6}-{\cfrac {bh^{3}}{6}}{6}H}}$	NA는 중립 축을 나타낸다.
다이아몬드		${\displaystyle S={\cfrac {BH^{2}}:{24}}}$	NA는 중립 축을 나타낸다.
C-채널		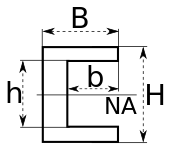${\displaystyle S={\cfrac {BH^{2}}-{6}-{\cfrac {bh^{3}}{6}}{6}H}}$	NA는 중립 축을 나타낸다.

플라스틱단면계수

플라스틱 단면 계수는 탄성 수율이 허용되고 플라스틱 동작이 허용 한계로 가정되는 재료에 사용된다.설계는 일반적으로 영구적인 변형을 방지하기 위해 궁극적으로 플라스틱 한계 이하로 유지되도록 노력하며, 플라스틱 용량을 증폭된 힘이나 응력과 비교한다.

플라스틱 단면 계수는 플라스틱 중립 축(PNA)의 위치에 따라 달라진다.PNA는 압축된 부위의 압축력이 장력에 있는 부위의 장력력과 같도록 단면을 분할하는 축으로 정의된다.따라서 지속적인 응력이 발생하는 섹션의 경우 PNA 위와 아래의 영역이 동일하지만 복합 섹션의 경우 반드시 그렇지는 않다.

플라스틱 단면 계수는 PNA의 각 면에 있는 단면적의 면적(같을 수도 있고 같지 않을 수도 있음)에 두 영역의 국부 중심에서 PNA까지의 거리를 곱한 값이다.

${\displaystyle Z_{P}=A_{C}y_{C}+A_{{}T}y_{T}}$

플라스틱 단면 계수는 '영역의 첫 순간'이 아니다.둘 다 중심 계산과 관련이 있지만, 플라스틱 단면계수는 PNA(플라스틱 중성축)의 양쪽에 있는 모든 면적의 합이며, 해당 면적의 중심에서 단면 중심까지의 거리로 곱한 반면, 면적의 첫 모멘트는 "포도 고려"의 어느 한 면을 기준으로 계산된다.단면의 "int"이며 단면을 따라 다르며 고려 지점에 따라 달라진다.

설명	피겨	방정식	댓글
직사각형 단면		${\displaystyle Z_{P}={\cfrac {bh^{2}}{4}}}}$[5][6]	${\$$T}={\cfrac {bh}{2}},$ $y{\displaystyle {}_{}}$ ${\displaystyle C_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle T_{}}$= ${\displaystyle \frac{h}{}}$ ${\displaystyle \frac{4}{}}$ ${\$$T}={\cfrac {h}{4}}}$
직사각형 중공 단면		${\displaystyle Z_{P}={\cfrac {bh^{2}}-(b-2t)\왼쪽({\cfrac {h}{2}}-t\오른쪽)^{2}}$	여기서: b = 폭, h = 높이, t = 벽 두께
웹이 제외된[7] I빔의 두 플랜지에 대해		${\displaystyle Z_{P}=b_{1}t_{1}y_{1}y_{1}+b_{2}t_{2}y_{2}y_{2}\,}$	여기서: ${\displaystyle b_{}}$$$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}$$= $$너비${\displaystyle {}_{}}$ t ${\displaystyle {1\mathrm{}}_{}}$, t ${\displaystyle {}_{}}$ ${\$}}$$=195, y ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$y ${\displaystyle {2\mathrm{}}_{}}$ ${\$}} 각각 플랜지의 중심에서 거리인 것이다.
웹을 포함한 I 빔의 경우		${\displaystyle Z_{P}=bt_{f}(d-t_{f})+0.25t_{w}(d-2t_{f})^{2}}$	[8]
I 보의 경우(취약 축)		${\displaystyle Z_{P}=(b^{2}t_{f}/2+0.25t_{w}^{2}(d-2t_{f})}}$	d = I 빔의 전체 높이
솔리드 서클		${\displaystyle Z_{P}={\cfrac {d^{3}}{6}}}$
원형 중공 단면		${\displaystyle Z_{P}={\cfrac {d_{2}^{3}-d_{1}^{3}}{6}}}}$

플라스틱 단면 계수는 단면의 플라스틱 모멘트, M 또는_p 전체 용량을 계산하는 데 사용된다.두 용어는 해당 물질의 항복 강도 F에_y 의해_p M = F_y z Z에 의해 관련된다.플라스틱 단면 계수와 탄성 단면 계수는 재료의 탄성 한계를 초과하는 용량 표시에 사용되는 k로 나타낼 수 있는 형상 계수에 의해 관련된다.이것은 수학적으로 다음과 같은 공식으로 보여질 수 있다.

${\displaystyle k={\cfrac {Z}{S}}}$

직사각형 단면의 형상 계수는 1.5이다.

구조 엔지니어링에 사용

이 절은 출처를 인용하지 않는다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션을 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다.(2014년 1월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

일반적으로 섹션 계수는 벤딩 빔의 극한 인장 또는 압축 섬유에 대해 계산되지만, 종종 휨 비틀림(F/T) 버클링의 시작 때문에 압축이 가장 중요한 경우다.일반적으로 (콘크리트와 같은 부서지기 쉬운 재료를 제외하고) 인장 극한 섬유는 압축 섬유보다 허용 응력이나 용량이 더 높다.

T-섹션의 경우 T-섹션 하단에 인장 섬유가 있는 경우, 중성축으로부터 일반적으로 훨씬 더 큰 거리로 인해 상단의 압축 섬유보다 더 중요할 수 있으므로 허용 가능한 응력이 더 높더라도 탄성 단면 계수 또한 더 낮다.이 경우 빔 길이와 구속장치는 압축 부재의 허용 응력 또는 용량을 감소시킬 수 있으므로 F/T 버클링이 여전히 평가되어야 한다.

직교축과 주축에 대한 값이 다르고 주축의 각도 구간이 같지 않은 경우 등 고려가 필요한 여러 가지 중요한 경우가 있을 수 있다.

보수적인 (안전한) 설계의 경우 토목 구조 엔지니어는 하중을 잘 이해하면 장력과 압축을 위해 다른 구간 계수를 활용할 수 있지만 빔을 따라 주어진 구간 역에 대해 최대 하중(텐실 또는 압축성)과 최저 탄성 구간 계수의 조합에 종종 관심을 갖는다.디자인에서 더 많은 것을 얻다설계가 체중 절감을 위해 훨씬 덜 보수적이어야 하는 항공 및 우주 애플리케이션의 경우 구조 분석에만 의존하는 것이 정당화하기가 더 어렵기 때문에(그리고 비용이 많이 들기 때문에) 안전성을 보장하기 위해 구조 시험이 종종 필요하다.

참고 항목

• 빔 이론
• 관성 영역 모멘트 목록
• 면적의 두 번째 모멘트

참조