위성 내비게이션 솔루션

수신자의 위치(게오 포지셔닝)를 위한 위성 내비게이션 솔루션에는 알고리즘이 포함됩니다.본질적으로 GNSS 수신기는 4개 이상의 GNSS 위성으로부터 방출되는 GNSS 신호의 송신시간을 측정하고(의사주파수를 부여한다), 이러한 측정은 그 위치(즉 공간좌표) 및 수신시간을 얻기 위해 사용된다.

계산 단계

글로벌 내비게이션 시스템(GNSS) 수신기는 4개 이상의 GNSS 위성( $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\,n$ $=$ 1, $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\,n$ , $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\,n$ , $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\,n$ 4, $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\,n$ . $\displaystyle i\;=\;1,\,2,\,3,\,4,\,..,\,n$ , $n,$ \ $display style$ i, $1$ $)$ 에서 방출되는 GNSS 신호의 겉보기 전송 $\displaystyle {\tilde {t}}_{i}$ $\displaystyle {\tilde {t}}_{i}$ ~ $i \style$ \ $displaystyle$ \displaystyle \tdisplaystyle \ $t}_{i$ 또는 "phase"를 측정합니다.동시에.^[1]
위성(예: 표시)의 메시지(예:{n1}:{n1}:{n1}:{n1}:{n1}, 텍스트(를)를)를) 표시합니다.i}(를) 표준 시간(T) 표준 시간(T) 표준 시간) 표준 시간, e.GPST^[2]
따라서 GNSS 위성신호의 $\displaystyle t_{i}$ $ti(\$ displaystyle $\displaystyle t_{i$ 는 비폐쇄형 $\displaystyle {\tilde {t}}_{i}\;=\;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i})$ t ~ $\displaystyle {\tilde {t}}_{i}\;=\;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i})$ $=$ $\displaystyle {\tilde {t}}_{i}\;=\;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i})$ + $\displaystyle {\tilde {t}}_{i}\;=\;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i})$ $\displaystyle {\tilde {t}}_{i}\;=\;t_{i}\,+\,\delta t_{{\text{clock}},i}(t_{i})$ ( $)\$ { $t}_{i$ }\;=\ $t_{$ clock $}$ 에서 도출됩니다. $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ ( $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ i ) $=$ $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ i $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ ( $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ ) $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ + $t-displaystyle$ \ $displaystyle \{\$ text{ $clock},i}(t_{i$ }\;\ $clock{\clock$ }i $},i$ }( ${\clock}$ i},{\clock},{\ $clock$ }, {\clock}, {\ $clock$ }, {\clock $\displaystyle \delta t_{{\text{clock}},i}(t_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},\,i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ 여기서 $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ t $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ , $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ ( $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ i , $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ i $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ ){ $displaystyle \delta t_{\text{orbit-rativ}},i}({\boldsymbol {r}}_{i},$ {\ $dot {\boldsymbol$ {r}}}}_{i $})$ 는 $\displaystyle \delta t_{{\text{orbit-relativ}},i}({\boldsymbol {r}}_{i},\,{\dot {\boldsymbol {r}}}_{i})$ 지구 궤도 및 이심률에서 주기적으로 상승한 상대론적 클럭 바이어스입니다.위성의 위치와 속도는 다음과 같이 $(\displaystyle$ \ $displaystyle$ $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ ${i$ })에 $\displaystyle t_{i}$ $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ 결정됩니다. $r$ i $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ $\displaystyle {\boldsymbol {r}}_{i}\;=\;{\boldsymbol {r}}_{i}(t_{i})$ ( $\displaystyle {\boldsymbol {r}}_{i}\;=\;{\boldsymbol {r}}_{i}(t_{i})$ ) \ displaystyle \ $displaystyle$ ${r} _$ { i } \ ; $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ \ ; { \ $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ ${$ r } $_$ { r （ t _ i } } （ t _ { i $\displaystyle {\boldsymbol {r}}_{i}\;=\;{\boldsymbol {r}}_{i}(t_{i})$ } $}$ ） } ） $\displaystyle {\dot {\boldsymbol {r}}}_{i}\;=\;{\dot {\boldsymbol {r}}}_{i}(t_{i})$ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ${{boldsymbol {r}}_{i}\;=\;{\dot {boldsymbol {r}}_{i}(t_{i$
GNSS 필드에서는 "geometric range", $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})$ ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})$ , $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})$ ){ $displaystyle$ \ $displaystyle$ r ( { \ $bold$ symbol { $r$ } $_$ { A } , { \ $bold$ symbol ${r} _$ { B $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})$ } $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})$ } )는 직선 범위 또는 3차원 ^[3]거리로 정의됩니다. $\displaystyle {\boldsymbol {r}}_{A}$ ^[2]프레임이 아닌 관성 프레임(예: 지구 중심 관성 $($ ECI) 1개)의 r A $(\$ displaystyle { $r}$ $_{A$ $})$ 에서 $\displaystyle {\boldsymbol {r}}_{A}$ r $(\displaystyle\displaystyle$ { $r}$ _{B $})$ 로 $\displaystyle {\boldsymbol {r}}_{B}$ $\displaystyle {\boldsymbol {r}}_{A}$ 합니다.
수신자의 위치 $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ r $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ \ $displaystyle \displaystyle \displaystyle {r}$ _ $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ text{rec}} 및 수신 $\displaystyle t_{\text{rec}}$ $\displaystyle t_{\text{rec}}$ {\ $displaystyle t_{\text{rec$ 은 r $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ )의 광원추방정식을 충족합니다. $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ r $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ rec ) $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ / $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ + ( $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ i - $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ rec ) $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ { \ $displaystyle$ \ $displaystyle$ rc\ $bold symbol {r} _$ { $rc}$ , { \ text { $rec$ } / c , + , （ $t _$ i } - $text$ { $rec$ } ） \ ; = \ $0$ 。여기서 $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}-t_{\text{rec}})\;=\;0$ $\displaystyle c$ c $\ display$ styledisplay styledisplay $style$ 의 속도입니다.위성에서 수신기로의 비행 신호 시간은 - $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$ ( $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$ i - $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$ rec $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$ ) { $displaystyle$ \ $displaystyle -$ ( $t$ _ { i , - , - , t _ { \ $text$ { rec $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$ } } $\displaystyle -(t_{i}\,-\,t_{\text{rec}})$
위는 위성항법식 $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ ( $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ , $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ ) / $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ + ( $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ - $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ ) + $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ t $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ - $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ t $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ - $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ err , $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ $\displaystyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})/c\,+\,(t_{i}\,-\,t_{\text{rec}})\,+\,\delta t_{{\text{atmos}},i}\,-\,\delta t_{{\text{meas-err}},i}\;=\;0$ \ $displaystyle$ r4 \ $boldsymbol {r}_{r}, {\text{$ rec}, { $c},$ {c}+c}/로 확장되었습니다. $\sec$ t_ ${\text{meas-err},i},-,\sec t_{\text{meas-err$ $\displaystyle \delta t_{{\text{meas-err}},i}$ $i}\;0$ 여기서 $\displaystyle \delta t_{{\text{atmos}},i}$ t $\$ \ $displaystyle t_{\$ text ${$ mapos $},i$ }, $\displaystyle \delta t_{{\text{meas-err}},i}$ $}$ 는 $\displaystyle \delta t_{{\text{atmos}},i}$ 측정 $\displaystyle \delta t_{{\text{meas-err}},i}$ 에 따른 대기 $\displaystyle \delta t_{{\text{meas-err}},i}$ 입니다 $.$ $i}}$ 는 $\displaystyle \delta t_{{\text{meas-err}},i}$ 측정 오차입니다.
Gauss-Newton 메서드는 솔루션의 비선형 최소 지연 문제를 해결하기 $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ 위해 $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ 할 $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ ( $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ ^ $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ , t $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ ) $=$ arg $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ ( $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ rec , $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ rec $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})\;=\;\arg \min \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})$ ) { $display$ style { r $}$ _ { \ $text$ { $rec$ } , { \ $hat$ { $text$ { rec $}$ , \ text { $rec$ } \ min ; \ $hat$ ）。 $t_{\text{rec$ 여기서 $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ ( $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ rec , $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ ) $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ ii $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ n ( $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ t $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ - $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ , $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ i / $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ meas t $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ - $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ , $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ i ) $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ \ $displaystyle$ \ $phi$ ( \ $boldsymbol { rec$ } $_$ { rec} , $text$ { $rec$ } , t _ { \ text { $rec$ } } } = $\displaystyle \phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}})\;=\;\sum _{i=1}^{n}(\delta t_{{\text{meas-err}},i}/\sigma _{\delta t_{{\text{meas-err}},i}})^{2}$ 1 ; \ $sum$ = 1 ; $\displaystyle \delta t_{{\text{meas-err}},i}$ $\displaystyle \delta t_{{\text{meas-err}},i}$ , $\displaystyle \delta t_{{\text{meas-err}},i}$ i \ $displaystyle \delta t_{\text{meas-err},$ i $}}$ 는 $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ \displaystyle \ $displaystyle$ { $r}_{\$ text ${$ rec $\displaystyle t_{\text{rec}}$ $\displaystyle t_{\text{rec}}$ trec $\displaystyle$ \ $displaystyle tyle$ tyle t_ ${r$ }의 $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ 함수로 간주해야 합니다.
$\displaystyle {\boldsymbol {r}}_{\text{rec}}$ rec \ $displaystyle \displaystyle {r}_$ $rec$ $}}$ $\displaystyle t_{\text{rec}}$ $\displaystyle t_{\text{rec}}$ {\ $displaystyle t_{\$ text ${$ rec}}}의 $\displaystyle t_{\text{rec}}$ $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$ $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$ 는 exp $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$ ( - $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$ $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$ $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$ ( $\displaystyle \exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))$ , $trec$ { $displaystyle$ \ exp ( - { - { - { - { - { \ $frac$ } \ frac { \ $frac }$ ) { rec } )\ $flac$ { rec } \ sylac { rec } } } } \ $sy$ $t_{\text{rec$ 모드는 $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ ( $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ ^ $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ , $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ ^ $\displaystyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ ), { $displaystyle \displaystyle$ {\ $hat {boldsymbol$ {r $}}_{\text{rec}}}},$ {\ $hat {text{rec$ 입니다.그들의 추론은 최대 사후 추정으로 공식화된다.
$\displaystyle {\boldsymbol {r}}_{\text{rec}}$ rec \ $displaystyle \displaystyle$ \ $displaystyle {r}$ _{\ $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ {rec $}}$ 의 $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ 후방 분포는 " $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$ - $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$ " $"$ ( - $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$ $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$ $\displaystyle {\boldsymbol {r}}_{\text{rec}}$ $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$ ( $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$ , t $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$ ) $displaystyle \int$ _ { - \ $infty }^{$ - infty } \ exp ( \ $frac$ { $ph }$ )에 비례합니다. $t_{\text{rec}}}), dt_{\text{$ rec $\displaystyle \int _{-\infty }^{\infty }\exp(-{\frac {1}{2}}\phi ({\boldsymbol {r}}_{\text{rec}},\,t_{\text{rec}}))\,dt_{\text{rec}}$

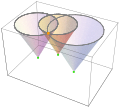
솔루션 그림

기본적으로 솔루션 $\scriptstyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ $\scriptstyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ ^ $\scriptstyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ , $\scriptstyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ ^ $\scriptstyle ({\hat {\boldsymbol {r}}}_{\text{rec}},\,{\hat {t}}_{\text{rec}})$ $){$ $displaystyle \scriptstyle ({\hat {boldsymbol {r}}_{\text{rec$ 은 광원뿔의 교집합입니다.
용액의 후방 분포는 전파하는 구면 분포의 곱에서 도출된다.(애니메이션 참조).

GPS 케이스

위성위치확인시스템(GPS)^[2]의 경우 스텝3의 비폐쇄형 방정식에 의해

\scriptstyle \scriptstyle \displaystyle \Delta t_{i}(t_{i},E_{i}),\triangleq \;t_{i},+,\text{clock},i},i},(t_{i}-,E_{i}-,{i},{\t},\tilde},{i},{i},{i},\},\},\},\,\},\,\,\,\,\cripti},\c

$\scriptstyle E_{i}$ 서 $(\displaystyle$ \ $scriptstyle E_{i$ })는 $\scriptstyle E_{i}$ $위성$ i(\ $displaystyle$ i $i$ 의 궤도 편심 이상, $(\$ $\scriptstyle$ $M_{$ $i$ })는 $\scriptstyle M_{i}$ 평균 편심 이상, $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ $(\$ \scriptstyle $e_{$ i $\scriptstyle e_{i}$ })는 편심, $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ i)입니다. $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ i ) $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ t $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ , $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ ( $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ ) + $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ t $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ - obliciv $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ , $\scriptstyle \delta t_{{\text{clock}},i}(t_{i},\,E_{i})\;=\;\delta t_{{\text{clock,sv}},i}(t_{i})\,+\,\delta t_{{\text{orbit-relativ}},i}(E_{i})$ ( $E$ ) \ $displaystyle \script$ style \ $t_{$ \ $text$ { $clock$ } , $i$ 、 i 、 = \ ; \ $deltelta t_{$ \ text { $clock }$ } 、 i （ t $+i$ ）

위의 문제는 $\$ } 및 $\scriptstyle t_{i}$ $\$ 에서 이변량 뉴턴-라프슨 방식을 사용하여 해결할 수 있습니다.대부분의 경우 2회 반복하면 충분합니다.반복 업데이트는 다음과 같이 야코비 행렬의 근사 역행렬을 사용하여 설명됩니다.

$\scriptstyle \scriptstyle \cisco {pmatrix}t_{i}\\E_{i}\\end{pmatrix}\왼쪽 화살표\begin{pmatrix}t_{i}\\E_{i}\\end{pmatrix}-{\begin{pmatrix}1&0\{\frac {\dot {M}}_{i}(t_{i}){1-e_{i}\cos E_{i}}&-{\frac {1-e_{i}\cos_{i}\}\{\}델타 t_{i}\\Delta M_{i}\\end{pmatrix}}$

GPS(Global Positioning System) 사양에^[2] 자세한 설명이 나와 있지 않지만 대류권 지연을 무시할 수 없습니다.

GLONASS 케이스

GLONASS 에페머라이드는 클럭 바이어스 $\scriptstyle \delta t_{{\text{clock,sv}},i}(t)$ $clock$ , $\scriptstyle \delta t_{{\text{clock,sv}},i}(t)$ $i$ ( $\scriptstyle \delta t_{{\text{clock,sv}},i}(t)$ $script$ { $clock$ , $sv$ } , $i$ } t clock clock $\scriptstyle \delta t_{{\text{clock}},i}(t)$ $clock$ 、 t $clock$ , $i$ ( t ) $\scriptstyle \delta t_{{\text{clock}},i}(t)$ t $clock$ , i ( t ) $\scriptstyle \delta t_{{\text{clock}},i}(t)$ 。

「」를 참조해 주세요.

첫 번째 수정 시간

메모들

GNSS 필드에서는 $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ ~ $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ $=$ - $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ ( $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ ~ $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ - $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ ~ $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ $){$ $displaystyle \scriptstyle \tilde {r}_{i}\;=\;cdisplaystyle$ \tilde { $t}_{i},-,-,{\text{$ rec $\scriptstyle {\tilde {r}}_{i}\;=\;-c({\tilde {t}}_{i}\,-\,{\tilde {t}}_{\text{rec}})$ }}}}}를 pseudorange라고 부릅니다. $\scriptstyle {\tilde {t}}_{\text{rec}}$ ~ $\scriptstyle {\tilde {t}}_{\text{rec}}$ rec \ $displaystyle \scriptstyle \tilde {t}_{\text {rec}}$ 은 $\scriptstyle {\tilde {t}}_{{{\text{rec}}}}$ 수신자의 잠정 수신 시간입니다. $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\,-\,t_{\text{rec}}$ t $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\,-\,t_{\text{rec}}$ , rec $=$ $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\,-\,t_{\text{rec}}$ ~ $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\,-\,t_{\text{rec}}$ - $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\,-\,t_{\text{rec}}$ t $rec$ rec { $displaystyle$ \ $scriptstyle t_{\text{clock$ ,rec}\;{\ $tilde {trec}},-,t_{\text{rec$ }}}}는 $\scriptstyle \delta t_{\text{clock,rec}}\;=\;{\tilde {t}}_{\text{rec}}\,-\,t_{\text{rec}}$ 수신자의 클럭 바이어스(즉,^[1] 클럭 어드밴스)라고 불립니다.
표준 GNSS 리시버는 관찰 에폭마다 $\scriptstyle {\tilde {r}}_{i}$ r ~ $\scriptstyle {\tilde {r}}_{i}$ \ $scriptstyle {r}_$ ${$ i $\scriptstyle {\tilde {r}}_{i}$ } $\scriptstyle {\tilde {t}}_{\text{rec}}$ 및 $\scriptstyle {\tilde {t}}_{\text{rec}}$ ~ $rec$ \displaystyle $\scriptstyle {t}_{\text{rec}}$ 를 $\scriptstyle {\tilde {t}}_{{{\text{rec}}}}$ $\scriptstyle {\tilde {r}}_{i}$ 합니다.
위성의 상대론적 클럭 바이어스의 시간적 변화는 궤도가 원형일 경우 선형이다(따라서 속도는 관성 프레임에서 균일하다).
위성에서 수신기로의 비행 신호 시간은 - $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ ( $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ - $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ ) $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ ~ $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ / $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ + $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ t $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ , $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ - $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ t clock , $\scriptstyle -(t_{i}-t_{\text{rec}})\;=\;{\tilde {r}}_{i}/c\,+\,\delta t_{{\text{clock}},i}\,-\,\delta t_{\text{clock,rec}}$ rec \ $display$ style - ( $t$ _ { $i$ } - t $_$ { \ $text$ { $rec$ } ) \ ; = \ ; { \ $tilde$ { r $} _$ { $i }$ / $clock$ ,오른쪽이 계산 시 반올림 오류 저항입니다.
기하학적 범위는 $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ r ( $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ , $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ rec ) $=$ $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ ( t $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ - $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ rec ) $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ i , $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ , $ECEF$ ( \ $displaystyle$ \script $style$ r4 $\boldsymbol {r}_{i},$ {\ $boldsymbol {$ r $}_r}\text{rec$ }\Omega ; \Omega ; \ $Omega)$ 로 계산됩니다. $ECEF}}},-,{\boldsymbol {r}}_{\text{rec$ ,ECEF $\scriptstyle r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})\;=\;|\Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}}){\boldsymbol {r}}_{i,{\text{ECEF}}}\,-\,{\boldsymbol {r}}_{\text{rec,ECEF}}|$ 여기서 지구중심 Earth-Fixed(ECEF) 회전 프레임(WGS84 또는 ITRF 등)은 오른쪽과 \ $SCript$ 스타일의 $\DISPLAY$ \DISPLAY $(\$ text{rec,\ $text$ {rec,ECEF}}}}}})가 사용됩니다.E $}}}$ 은 $\scriptstyle \Omega _{{{\text{E}}}}$ (는) 신호 전달 시간을 ^[2]인수로 하는 지구 회전 행렬입니다.매트릭스는 $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ E ( $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ - t $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ ) $=$ E ( $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ t $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ , $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ rec ) $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ E $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ ( - $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ ~ $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ / $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ - $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ clock , $\scriptstyle \Omega _{\text{E}}(t_{i}\,-\,t_{\text{rec}})\;=\;\Omega _{\text{E}}(\delta t_{\text{clock,rec}})\Omega _{\text{E}}(-{\tilde {r}}_{i}/c\,-\,\delta t_{{\text{clock}},i})$ ){ $display$ style \ $Omega _{I}}$ ( $t_{i}-, t_{$ text\rec})로 인수분해할 수 있습니다. $\Omega$ _ ${\text{E}}(-{\tilde {r}_{i}/c,-,\delta t_{\text{clock},i$
$\scriptstyle {\boldsymbol {r}}_{\text{rec,ECEF}}$ \ $scriptstyle$ ${r}_{\text{rec,ECEF}}$ 에서 $\scriptstyle {\boldsymbol {r}}_{{{\text{rec,ECEF}}}}$ 관측된 위성의 가시 단위 $\scriptstyle {\boldsymbol {e}}_{i,{\text{rec,ECEF}}}\;=\;-{\frac {\partial r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})}{\partial {\boldsymbol {r}}_{\text{rec,ECEF}}}}$ 는 $\scriptstyle {\boldsymbol {e}}_{i,{\text{rec,ECEF}}}\;=\;-{\frac {\partial r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})}{\partial {\boldsymbol {r}}_{\text{rec,ECEF}}}}$ $\scriptstyle {\boldsymbol {e}}_{i,{\text{rec,ECEF}}}\;=\;-{\frac {\partial r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})}{\partial {\boldsymbol {r}}_{\text{rec,ECEF}}}}$ - $\scriptstyle {\boldsymbol {e}}_{i,{\text{rec,ECEF}}}\;=\;-{\frac {\partial r({\boldsymbol {r}}_{i},\,{\boldsymbol {r}}_{\text{rec}})}{\partial {\boldsymbol {r}}_{\text{rec,ECEF}}}}$ rec $,$ style로 $표현된다.$ $ECEF}}\;=\;-{\frac$ {\ $boldsymbol {r}_{i},{\boldsymbol {r}_{\text{rec}}}}{\text{rec,ECEF$
위성항법식에는 $(\$ style { $r}_$ $\scriptstyle {\boldsymbol {r}}_{\text{rec,ECEF}}$ 와 " $\scriptstyle \delta t_{\text{clock,rec}}$ clock, $\$ 변수를 사용합니다.
대류권 지연의 수직 의존성의 비선형성은 7단계에서 가우스-뉴턴 반복의 수렴 효율을 저하시킨다.
위 표기법은 위성위치확인시스템(GPS)의 위키피디아 기사 '위치계산 소개' '위치계산 고급'과 다르다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b Misra, P. 및 Enge, P., 글로벌 포지셔닝 시스템:신호, 측정, 성능, 2차, 간가자무나 프레스, 2006.
^ ^a ^b ^c ^d ^e ^f NAVSTAR 위성위치확인시스템 인터페이스 사양
^ 3차원 거리는 $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ , $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ r $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ A - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ B ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ 2 + ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ 2 + ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ A - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ 2 \ $display$ style \ $display style$ rsyl \ bold $symbol {r}_A},$ {A}, ${{boldsymbol {r}}_{B}={\boldsymbol {r}_{A}-{B}={smbrt {(x_{A}-x_{B})^2}+(y_{})$ $A}-y_{B}^{2}+(z_{)$ $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $}-z_{B}^{2}}}:$ $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $=$ ( $x$ $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ , $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ , $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $){$ { $r}_{$ A}=( $x_{A}$ , z_{ $A}})$ 및 $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ ( $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ B , $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ bold $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ , $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ $styledisplay$ B $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ \style )

외부 링크

PVT(위치, 속도, 시간):오픈 소스 GNSS-SDR 및 기본 RTKLIB 계산 절차

[Misra_Enge-1] Misra, P. 및 Enge, P., 글로벌 포지셔닝 시스템:신호, 측정, 성능, 2차, 간가자무나 프레스, 2006.

[IS-GPS-2] ^ ^a ^b ^c ^d ^e ^f NAVSTAR 위성위치확인시스템 인터페이스 사양

[3] 3차원 거리는 $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ , $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ r $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ A - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ B ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ 2 + ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ 2 + ( $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ A - $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ ) $\displaystyle r({\boldsymbol {r}}_{A},\,{\boldsymbol {r}}_{B})=|{\boldsymbol {r}}_{A}-{\boldsymbol {r}}_{B}|={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}+(z_{A}-z_{B})^{2}}}$ 2 \ $display$ style \ $display style$ rsyl \ bold $symbol {r}_A},$ {A}, ${{boldsymbol {r}}_{B}={\boldsymbol {r}_{A}-{B}={smbrt {(x_{A}-x_{B})^2}+(y_{})$ $A}-y_{B}^{2}+(z_{)$ $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $}-z_{B}^{2}}}:$ $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $=$ ( $x$ $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ , $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ , $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $){$ { $r}_{$ A}=( $x_{A}$ , z_{ $A}})$ 및 $\displaystyle {\boldsymbol {r}}_{A}=(x_{A},y_{A},z_{A})$ $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ ( $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ B , $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ bold $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ , $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ $styledisplay$ B $\displaystyle {\boldsymbol {r}}_{B}=(x_{B},y_{B},z_{B})$ \style )

[1]

[2]

[3]

Search

위성 내비게이션 솔루션

네임스페이스

더

목차

계산 단계

솔루션 그림

GPS 케이스

GLONASS 케이스

「」를 참조해 주세요.

메모들

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

위성 내비게이션 솔루션

계산 단계

솔루션 그림

GPS 케이스

GLONASS 케이스

「 」를 참조해 주세요.

메모들

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.

「」를 참조해 주세요.