각도를 통한 좌표 변환
xy-Cartesian 좌표계가 각도 θ {\displaystyle \theta} x'Cartesian 좌표계로 회전함 수학 에서 2차원의 축 회전 은 xy-카르트 좌표계 에서 x'-카르트 좌표계로 매핑하는 것으로, x'-카르트 좌표계로 원점 이 고정되어 있고 x' 와 y' 축이 각 θ {\displaystyle \ta}}} x 와 y축 을 시계 반대방향으로 회전시켜 얻어진다. p점 에는 좌표(x , y)가 있다.h 원래 시스템에 대한 존중 및 새 시스템에 대한 좌표([1] x', y') 새로운 좌표계에서는 P 지점이 θ {\displaystyle \theta } . [2] [3] 축의 회전은 선형 지도 와[4] [5] 경직된 변환 이다.
동기 좌표계는 분석 기하학 의 방법을 사용하여 곡선 의 방정식을 연구하는데 필수적이다. 좌표 지오메트리의 방법을 사용하기 위해, 고려 중인 곡선과 관련하여 축을 편리한 위치에 배치한다. 예를 들어 타원 과 하이퍼볼라 의 방정식을 연구하기 위해 포커스 는 보통 축들 중 하나에 위치하며 원점에 관해서 대칭적으로 위치한다. 곡선(하이퍼볼라, 파라볼라 , 타원 등)이 축에 대해 편리하게 위치하지 않는 경우, 편리하고 익숙한 위치와 방향에 곡선을 배치하도록 좌표계를 변경해야 한다. 이런 변화를 만드는 과정을 좌표 변환 이라고 한다.[6]
좌표 축을 회전시켜 동일한 원점을 통해 새로운 축을 획득함으로써 많은 문제에 대한 해결책을 단순화할 수 있다.
파생 xy 축을 x'y' .
xy 시스템에서 P 지점 에 극좌표 (r α {\displaystyle(r,\alpha )} . 그런 다음 x'y' 시스템에서 P 는 극좌표(r , α θ {\displaystyle (r,\alpha \theta )} .
삼각함수 를 이용하여, 우리는
x = r cas α \displaystyle x=r=r\cos \cos \cos (1 )
y = r 죄를 짓다 α \displaystyle y=r\sin \cHB \cHB (2 )
그리고 차이점들을 위해 표준 삼각공식을 사용하여, 우리는
x ′ = r cas ( α − θ ) = r cas α cas θ + r 죄를 짓다 α 죄를 짓다 θ \displaystyle x'=r\cos(\displaystyle -\theta )=r\cos \cos \cos \coses \coses \coses \coses \cos \coses \cos (3 )
y ′ = r 죄를 짓다 ( α − θ ) = r 죄를 짓다 α cas θ − r cas α 죄를 짓다 θ . \displaystyle y'=r\sin(\displaystyle -\theta )=r\sin \coses \theta -r\coses \coses \coses \sin \sin \theta.} (4 )
등식 등식
x ′ = x cas θ + y 죄를 짓다 θ \displaystyle x'=x\cos \theta +y\sin \theta } (5 )
y ′ = − x 죄를 짓다 θ + y cas θ . \displaystyle y'=-x\sin \theta +y\cos \theta.} [7] (6 )
방정식 (5 6
( x ′ y ′ ) = ( cas θ 죄를 짓다 θ − 죄를 짓다 θ cas θ ) ( x y ) , {\displaystyle {\pmatrix}x'\\y'\end{pmatrix}={\\pmatrix}={\pmatrix}={\theta \\\sin \theta \end{pmatrix}},},} 2차원에서 축의 회전에 대한 표준 행렬 방정식은 다음과 같다.[8]
역변형은
x = x ′ cas θ − y ′ 죄를 짓다 θ \displaystyle x=x'\cos \theta -y'\sin \theta } (7 )
y = x ′ 죄를 짓다 θ + y ′ cas θ , \displaystyle y=x'\sin \theta +y'\cos \theta ,} [9] (8 )
또는
( x y ) = ( cas θ − 죄를 짓다 θ 죄를 짓다 θ cas θ ) ( x ′ y ′ ) . {\displaystyle {\pmatrix}x\\y\end{pmatrix}={\\\nd{pmatrix}cos \theta \\\\sin \pmatrix}cos \theta \end{pmatrix}}{pmatrix}}}}}. } 2차원의 예 예 1 축이 θ 1 π x 3 1 {\displaystyle P_{1}=(x,y)=({\sqrt{3},1 P1 6 {\displaysty theta _{1}=\pi /6} °
해결책:
x ′ = 3 cas ( π / 6 ) + 1 죄를 짓다 ( π / 6 ) = ( 3 ) ( 3 / 2 ) + ( 1 ) ( 1 / 2 ) = 2 {\displaystyle x'={\sqrt{3}\cos(\pi /6)+1\sin(\pi /6)=({\sqrt{3}/2)+(1/2)=2} y ′ = 1 cas ( π / 6 ) − 3 죄를 짓다 ( π / 6 ) = ( 1 ) ( 3 / 2 ) − ( 3 ) ( 1 / 2 ) = 0. {\displaystyle y'=1\cos(\pi /6)-{\sqrt {3}\sin(\pi /6)=(1)({\sqrt{3}/2)-({\sqrt{3})(1/2)=0). } The axes have been rotated counterclockwise through an angle of θ 1 = π / 6 {\displaystyle \theta _{1}=\pi /6} P 1 = ( x ′ , y ′ ) = ( 2 , 0 ) {\displaystyle P_{1}=(x',y')=(2,0)} π / 6 {\displaystyle \pi /6} 이제 (새) x' 축과 일치하도록 고정 축에 대한 존중
예 2 축이 시계 방향으로 90° 회전한 후, θ 2 π {\displaystyle \theta _{2}=-\pi } 또는 P2 x,y)=(7,7 .
해결책:
( x ′ y ′ ) = ( cas ( − π / 2 ) 죄를 짓다 ( − π / 2 ) − 죄를 짓다 ( − π / 2 ) cas ( − π / 2 ) ) ( 7 7 ) = ( 0 − 1 1 0 ) ( 7 7 ) = ( − 7 7 ) . {\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}\cos(-\pi /2)&\sin(-\pi /2)\\-\sin(-\pi /2)&\cos(-\pi /2)\end{pmatrix}}{\begin{pmatrix}7\\7\end{pmatrix}}={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}{\begin{pmatrix}7\\7\end{pmatrix}}={\begin{pmatrix}-7\\7\end{pmatrix}}. } The axes have been rotated through an angle of θ 2 = − π / 2 {\displaystyle \theta _{2}=-\pi /2} P 2 = ( x ′ , y ′ ) = ( − 7 , 7 ) {\displaystyle P_{2}=(x',y')=(-7,7)} 고정 π {\displaystyle \pi /2}.
원뿔단면 회전 2도의 가장 일반적인 방정식은 형태를 가지고 있다.
A x 2 B x y C y D x E F 0 {\displaysty Ax^{2}+Bxy+ Cy^{2}+Dx+Ey + [10] A, B , C {\displaystyle A,B,C} (9 )
좌표 변경(축 회전 및 축 변환 )을 통해 방정식(9 표준형식 으로 넣을 수 있어 통상적으로 작업하기 쉽다. 새로운 시스템에서는 x'y' 라는 용어가 없는 방식으로 좌표를 회전시키는 것이 항상 가능하다. 방정식
A ′ x ′ 2 + B ′ x ′ y ′ + C ′ y ′ 2 + D ′ x ′ + E ′ y ′ + F ′ = 0 , {\displaystyle A'x^{2}+B'xy'+C'y'^{2}+D'x'+E'+++ F'=0,} (10 )
어디에
A ′ = A cas 2 θ + B 죄를 짓다 θ cas θ + C 죄를 짓다 2 θ , (\displaystyle A'= A\cos ^{2}\theta +B\sin \cos \theta \theta +C\sin ^{2}\theta ,} B ′ = 2 ( C − A ) 죄를 짓다 θ cas θ + B ( cas 2 θ − 죄를 짓다 2 θ ) , {\displaystyle B'=2(C-A)\sin \theta \cos \coses \theta +B(\coses ^{2}\theta -\sin ^{2}\theta }),} C ′ = A 죄를 짓다 2 θ − B 죄를 짓다 θ cas θ + C cas 2 θ , \displaystyle C'=A\sin ^{2}\theta -B\sin \coses \coses \theta +C\coses ^{2}\theta ,} D ′ = D cas θ + E 죄를 짓다 θ , \displaystyle D'=D\cos \theta +E\sin \theta ,} E ′ = − D 죄를 짓다 θ + E cas θ , \displaystyle E'=-D\sin \theta +E\coses \theta ,} F ′ = F . F'=F. } (11 )
θ {\displaystyle \theta } ( 요람 cot θ A displaystyle \cot \theta A-C)/B} B ′ 0 {\displaysty B'=0} 10 'y 항이 사라진다.[11]
B , D , E 가 모두 0과 다른 문제가 발생했을 때, 연속적으로 회전(B 제거)과 번역(D , E 용어 제거)을 수행하여 제거할 수 있다.[12]
회전 원뿔 단면 식별 등식 (9 2 4 C {\displaystyle ^{2}\ 4AC} . 원뿔 부분은 다음과 같다.
{ 타원이나 원 , 만일 B 2 − 4 A C < 0 ; 포물선. , 만일 B 2 − 4 A C = 0 ; 쌍곡선. , 만일 B 2 − 4 A C > 0. {\displaystyle {\begin{cases}{\mbox{an ellipse or a circle}},\ {\mbox{if}}\ B^{2}\ -\ 4AC\ <\ 0;\\{\mbox{a parabola}},\ {\mbox{if}}\ B^{2}\ -\ 4AC\ =\ 0;\\{\mbox{a hyperbola}},\ {\mbox{if}}\ B^{2}\ -\ 4AC\ >\ 0. \end{case}}} [13] 몇 가지 차원으로 일반화 직사각형 xyz-coordinate 시스템이 각도 positive {\displaystyle \theta }, 양 의 x 축이 즉시 양의 y 축으로 회전한다고 가정하자. 각 점의 z 좌표는 변경되지 않고 x 좌표 와 y 좌표는 위와 같이 변형된다. 점 Q 의 이전 좌표(x , y, z )는 다음에 의해 새로운 좌표(x ', y', z') 와 관련된다.
( x ′ y ′ z ′ ) = ( cas θ 죄를 짓다 θ 0 − 죄를 짓다 θ cas θ 0 0 0 1 ) ( x y z ) . {\displaystyle {\begin{pmatrix}x'\\y'\\z'\end{pmatrix}}={\begin{pmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}. } [14] 제한된 수의 차원으로 일반화하는 회전 행렬 A {\displaystyle A} ID 행렬 과 다른 직교 행렬 이다 이 네 가지 요소는 형식이다.
a j cos θ displaystyle a_{i}=a_{filename}=\cos theta } i j i sin i , {\displaystyle a_{ij}=-{ji}=\sin \theta ,} 일부 θ[\displaystyle \theta } i ≠ j .[15]
몇 가지 차원의 예 예 3 Find the coordinates of the point P 3 = ( w , x , y , z ) = ( 1 , 1 , 1 , 1 ) {\displaystyle P_{3}=(w,x,y,z)=(1,1,1,1)} w axis has been rotated through the angle θ 3 = π / 12 {\displaystyle \theta _{3}=\pi /12} z axis.
해결책:
( w ′ x ′ y ′ z ′ ) = ( cas ( π / 12 ) 0 0 죄를 짓다 ( π / 12 ) 0 1 0 0 0 0 1 0 − 죄를 짓다 ( π / 12 ) 0 0 cas ( π / 12 ) ) ( w x y z ) {\displaystyle {\begin{pmatrix}w'\\x'\\y'\\z'\end{pmatrix}}={\begin{pmatrix}\cos(\pi /12)&0&0&\sin(\pi /12)\\0&1&0&0\\0&0&1&0\\-\sin(\pi /12)&0&0&\cos(\pi /12)\end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}} ≈ ( 0.96593 0.0 0.0 0.25882 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 − 0.25882 0.0 0.0 0.96593 ) ( 1.0 1.0 1.0 1.0 ) = ( 1.22475 1.00000 1.00000 0.70711 ) . {\displaystyle \approx {\begin{pmatrix}0.96593&0.0&0.0&0.25882\\0.0&1.0&0.0&0.0\\0.0&0.0&1.0&0.0\\-0.25882&0.0&0.0&0.96593\end{pmatrix}}{\begin{pmatrix}1.0\\1.0\\1.0\\1.0\end{pmatrix}}={\begin{pmatrix}1.22475\\1.00000\\1.00000\\0.70711\end{pmatrix}}. } 참고 항목 메모들 ^ 프로토터 & 모레이(1970 , 페이지 320) 하프텍트 오류: 대상 없음: CATEREFProtter Morrey1970(도움말 ) ^ 안톤(1987 , 페이지 231)^ 부담&장자(1993 , 페이지 532)^ 안톤(1987 , 페이지 247)^ 보어가드 & 프랄리 (1973년 , 페이지 266년)^ 프로토터 & 모레이(1970 , 페이지 314–315) 하프텍스트 오류: 대상 없음: CITREFProtter Morrey1970(도움말 ) ^ 프로토터 & 모레이(1970 , 페이지 320–321) 하프텍스트 오류: 대상 없음: CITREFProtter Morrey1970 (도움말 )^ 안톤(1987 , 페이지 230)^ 프로토터 & 모레이(1970 , 페이지 320) 하프텍트 오류: 대상 없음: CATEREFProtter Morrey1970(도움말 ) ^ 프로토터 & 모레이(1970 , 페이지 316) 하프텍스트 오류: 대상 없음: CITREFProtter Morrey1970(도움말 ) ^ 프로토터 & 모레이(1970 , 페이지 321–322) 하프텍스트 오류: 대상 없음: CITREFProtter Morrey1970 (도움말 )^ 프로토터 & 모레이(1970 , 페이지 324) 하프텍스트 오류: 대상 없음: CATEREFProtter Morrey1970(도움말 ) ^ 프로토터 & 모레이(1970 , 페이지 326) 하프텍스트 오류: 대상 없음: CATEREFProtter Morrey1970(도움말 ) ^ 안톤(1987 , 페이지 231)^ 부담&장자(1993 , 페이지 532) 참조 Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley , ISBN 0-471-84819-0 Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields Houghton Mifflin Co. , ISBN 0-395-14017-X Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis Prindle, Weber and Schmidt , ISBN 0-534-93219-3 Protter, Murray H.; Morrey, Jr., Charles B. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley , LCCN 76087042 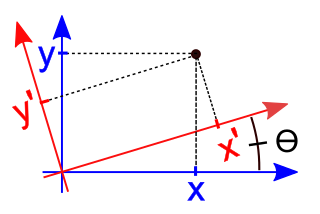
 통해 x'Cartesian 좌표계로 회전함
통해 x'Cartesian 좌표계로 회전함
































 되고 (
되고 (


 . 이 네 가지 요소는 형식이다.
. 이 네 가지 요소는 형식이다. 






