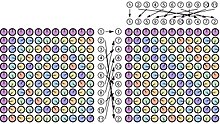
래더의 FFT 알고리즘

는 순환 상승이 DFT re-expressing에 의해 주요 사이즈의 이산 푸리에 변환(DFT)를 계산하 레이더의 알고리즘(1968년)[1]는 찰스 M. 레이더도 MIT링컨 연구소의 이름으로 명명된는 빠른 푸리에 변환(FFT)알고리즘(FFTs 크기의, Bluestein의 알고리즘의 다른 알고리즘도 DFT을 다시 작성한 사로 일한다nvolution.

래더의 알고리즘은 DFT 커널의 주기성에만 의존하므로, 숫자-이성 변환이나 이산형 하틀리 변환과 같은 유사한 속성을 가진 (주문 순서) 다른 변환에도 직접 적용할 수 있다.

알고리즘을 수정하여 실제 데이터의 DFT 사례에 대해 2개의 절약을 얻을 수 있으며, 실제 데이터의 절반 크기 주기적 교란을 얻기 위해 약간 수정된 재색인/주정을 사용할 수 있다.^[2] 실제 데이터의 DFT에 대한 대체 적응은 이산형 하틀리 변환을 사용한다.^[3]

Winograd는 프라임파워 ${\displaystyle {DFT}^{}}$ 크기 $p{\displaystyle {}^{}}$ m${\$^[4][5]를 포함하도록 Rader의 알고리즘을 확장시켰으며, 오늘날 Rader의 알고리즘은 때로는 훨씬 더 큰 크기의 클래스에 적용되는 승법 푸리에 변환 알고리즘(Tolimieri et al., 1997)^[6]이라고도 불리는 Winograder의 FFT 알고리즘의 특수한 사례로 설명되기도 한다.하지만, 프라임 파워와 같은 복합적인 크기의 경우, 쿨리-Tukey FFT 알고리즘은 훨씬 간단하고 구현이 실용적이기 때문에 Rader의 알고리즘은 일반적으로 Cooley-의 대형 프라임 베이스 케이스에만 사용된다.DFT에 대한 투키의 재귀적 분해.^[3]

알고리즘.

Rader의 FFT 알고리즘에서 DFT 매트릭스의 시각적 표현.배열은 크기 11의 DFT 행렬을 나타내는 색상의 시계로 구성된다.원근 11의 원근의 힘에 의해 생성된 순서에 따라 행과 열(각각의 첫 번째를 제외)을 허용함으로써 원래의 DFT 매트릭스는 순환 행렬이 된다.데이터 시퀀스에 순환 매트릭스를 곱하는 것은 매트릭스의 행 벡터와의 주기적 경련과 동일하다.이러한 관계는 승수군이 순환$({\displaystyle }$Z / p${\displaystyle Z{}^{}}$)${\displaystyle {}^{}}$ ≅${\displaystyle C_{}}$ - ${\displaystyle 1_{}}$ ${\$(\$mathb {Z} /p\mathb {Z} )^{\time }\cong C_{p-1$}$$.

이산 푸리에 변환의 정의부터 시작하십시오.

${\displaystyle X_{k}=\sum _{n=0}^{{N-1}x_{n}e^{-{\frac {2\pi i}{N}}{N}nk}\qquad k=0,\dots,N-1.}$

N이 소수인 경우, 0이 ${\displaystyle \mathrm{아닌}}$ 지수 $집합$은 n${\displaystyle \in \{}$ 1${\displaystyle }$,${\displaystyle }$… ,${\displaystyle N}$- ${\displaystyle 1}$ ${\displaystyle \}}$ ${\in {}\{1,\dots ,N-1\}}$이(가) 곱셈모듈로 그룹을 형성한다$$.그러한 집단의 수 이론의 한 가지 결과는 집단의 발생기(때로는 원시적 뿌리라고 불리기도 하는데, 이것은 철저한 검색이나 약간 더 나은 알고리즘에^[7] 의해 빠르게 발견될 수 있다.)가 존재한다는 것이다.이 생성기는 0이 아닌 모든 색인 n과 고유 $q{\displaystyle }$ ${\displaystyle \in }$ {${\displaystyle 0}$,${\displaystyle }$…${\displaystyle }$N${\displaystyle }$- ${\displaystyle 2}$$$${\displaystyle \}}$ ${\displaystyle q\in$ {$0,\dots ,$N-2$\}$에 대해 n${\displaystyle }$= ${\displaystyle {}^{}}$ q${\displaystyle {}^{}}$(${\displaystyle \mathrm{mod}}$ $){\$와 같은 정수 g이다.Similarly, ${\displaystyle k=g^{-p}{\pmod {N}}}$ for any non-zero index k and for a unique ${\displaystyle p\in {}\{0,\dots ,N-2\}}$, where the negative exponent denotes the multiplicative inverse of ${\displaystyle g^{p}\mod N}$. That means that we can rewrite 이러한 새로운 지수 p와 q를 다음과 같이 사용하는 DFT:

${\displaystyle X_{0}=\sum _{n=0}^{{N-1}x_{n}}}$

${\displaystyle X_{g^{-p}}=x_{0}+\sum _{q=0}^{{n-2}x_{g^{q}e^{-{\frac {2\pi i}{N}}}}}}}}g^{-{-(p-q)}}}}}\qquad p=0,\dots, N-2.}$

(X와_n X는_k N에서 암묵적으로 주기적이며, $e{\displaystyle {}^{}}$ ${\displaystyle 2^{}}$ ${\displaystyle i^{}}$i = ${\displaystyle 1}$ ${\displaystyle$ e$^{2\pi i}=$1}($$Euler의 ID)를 호출한다.따라서 모든 지수와 지수를 그룹 산술에서 요구하는 모듈로 N을 취한다.)

위의 최종 합계는 정확하게 다음과_q 같이 정의된 두 시퀀스 a와_q b(길이 N–1의 경우, $q{\displaystyle }$ ${\displaystyle \in }$ { ${\displaystyle 0}$,${\displaystyle }$… ,${\displaystyle N}$- ${\displaystyle 2}$ ${\displaystyle \}}$ ${\0,\dots ,N-2$의 주기적인 콘볼루션이다.

${\displaystyle a_{q}=x_{g^{q}}}$

${\displaystyle b_{q}=e^{-{\frac {2\pi i}{N}}g^{-q}}}$

콘볼루션 평가

N–1이 복합적이기 때문에, 이 경련은 콘볼루션 정리 및 더 전통적인 FFT 알고리즘을 통해 직접 수행될 수 있다.그러나 N–1 자체가 큰 주요 요인을 가지고 있어 Rader의 알고리즘을 재귀적으로 사용해야 한다면 이는 효율적이지 않을 수 있다.대신 최소 2(N–1)–1의 길이로 패딩하지 않고 정확하게 2(N–1)–1의 길이로 패딩함으로써 길이(N–1) 주기적 콘볼루션을 계산할 수 있으며, 라더의 알고리즘의 반복적 적용 없이 O(N 로그 N) 시간에 평가할 수 있다.

그러면 이 알고리즘은 O(N) 추가와 O(N 로그 N) 시간을 더하여 콘볼루션을 수행해야 한다.실제로 O(N) 추가는 종종 콘볼루션에 대한 추가를 흡수하여 수행할 수 있다: 콘볼루션이 FFT 쌍에 의해 수행되는 경우, x의_n 합은 플러스_q X의₀ FFT의 DC(0번째) 출력에 의해 주어지며, x는₀ 역 FFT 이전의 콘볼루션의 DC 용어에 추가하여 모든 출력에 추가할 수 있다.그러나 이 알고리즘은 본질적으로 인근 복합재 크기의 FFT보다 더 많은 연산을 필요로 하며, 일반적으로 실제 연산의 3~10배가 소요된다.

위에서 언급한 바와 같이 제로 패딩이 아닌 N–1 크기의 FFT를 사용하여 콘볼루션을 계산하면, 효율은 N과 레이더의 알고리즘을 재귀적으로 적용해야 하는 횟수에 크게 좌우된다.최악의 경우는 N-1이 N이₂ prime인 2N₂, N이₂₃ prime인 2N일₃ 경우일 것이다.그러한 경우, 프리타임 체인이 어떤 경계값까지 완전히 확장되었다고 가정할 때, 래더의 알고리즘의 재귀적 적용은 실제로 O(N²) 시간을^{[dubious – discuss]} 필요로 할 것이다.그런 N을_j 소피 제르맹 프리메인이라고 하며, 그 시퀀스를 제1종 커닝햄 체인이라고 한다.그러나 커닝햄 체인의 길이는 로그₂(N)보다 더 느리게 자라는 것이 관찰되므로, 이런 식으로 적용되는 래더의 알고리즘은 최악의 경우 O(N 로그 N)보다 더 나쁠 수 있지만 아마도 O(N²)는 아닐 것이다.다행히도, O(N 로그 N) 복잡성의 보장은 제로 패딩으로 달성할 수 있다.

참조