극분할

극분리는 전자 증폭기에 사용되는 주파수 보상의 어떤 형태로 악용되는 현상이다.주파수에서 가장 낮은 극(일반적으로 입력극)을 낮은 주파수로 이동시킬 목적으로 증폭기의 입력과 출력 측 사이에 캐패시터가 도입되면, 극 분할은 주파수에서 다음 극(일반적으로 출력 극)이 더 높은 주파수로 이동하게 한다.이 극의 움직임은 증폭기의 안정성을 증가시키고 속도 감소의 비용으로 스텝 응답을 향상시킨다.^[1][2][3][4]

폴 분할 예제

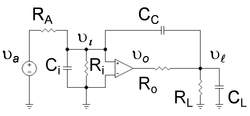
이 예는 그림 1의 증폭기에서 C라고_C 하는 콘덴서의 도입에 두 가지 결과가 있음을 보여준다. 첫째는 앰프의 가장 낮은 주파수 폴이 여전히 주파수에서 더 낮게 이동하게 하고, 둘째는 더 높은 폴이 주파수에서 더 높게 이동하게 한다.^[5]그림 1의 증폭기는 추가 입력 저항 R과_i 캐패시턴스 C로_i 인해 저주파 극을 가지며, 시간 상수 C_i(R_Ai R )는 다음과 같다.이 장대는 밀러 효과에 의해 빈번히 아래로 이동한다.앰프에는 부하 저항_L R과 캐패시턴스 C를_L 추가하여 고주파 출력 폴이 주어지며, 시간 상수_L C(R_oL R )는 다음과 같다.고주파극의 상향 이동은 밀러 증폭 보상 캐패시터 C가_C 출력 전압 분배기의 주파수 의존도를 변경하기 때문에 발생한다.

가장 낮은 극이 주파수에서 아래로 움직이는 것을 보여주기 위한 첫 번째 목표는 밀러의 정리 기사와 같은 접근법을 사용하여 확립된다.밀러의 정리 기사에 기술된 절차에 따라 그림 1의 회로는 그림 1과 전기적으로 동등한 그림 2의 회로로 변형된다.그림 2의 입력 측에 Kirchhoff의 현재 법칙을 적용하면 입력 전압 v i ${\$\$v_{i},$$$즉, 적용 신호 전압 v ${\displaystyle a_{}}$ ${\$\$v_{a}$의 함수로서 이상적인 op amp에 대한$$ 입력 전압 ${\displaystyle v_{}}$ {\displaystystyled \ v_{a},

${\displaystyle {\frac {v_{i}}{v_{a}}={\frac {R_{i}}{R_{i}}+R_{{}}}}{\fracA}}{\frac{1}{1+j\omega(C_{M}+C_{i})(R_{A}\ R_{i}}}}}}},}$

f에서₁ 시작하는 주파수에서 롤오프를 나타낸다.

${\displaystyle {\begin}f_{1}{1}&={\frac {1}{1\pi(C_{M}+C_{i})(R_{A}\R_{i}}}}}}\={\frac {1}{2\pi \1}\1}\\\ended}}}}}}}}}$

가장 낮은 극의 시간 상수에 대한$$ 표기법 $\tau {\displaystyle {}_{}}$ ${\$}을 도입한다.이 주파수는 앰프의 초기 저주파수보다 낮으며, C_C = 0F의 경우 1 ${\displaystyle \frac{2}{}}$㎛ ${\displaystyle \frac{{Ci}_{}{}_{}}{}}$ ${\displaystyle \frac{{}_{}{}_{}{r}_{}}{}}$ R${\displaystyle \frac{{}_{}}{}}$i $){\${\$frac${1$}{2\PI C_{i}(R_{A}\ R_{i$

더 높은 극의 움직임을 여전히 더 높은 주파수로 보여주는 두 번째 목표로 돌리면, 전체적인 이득에 두 번째 요인이 되는 회로의 출력측과 추가적인 주파수 의존성을 살펴볼 필요가 있다.전압 ${\displaystyle v{}_{}}$ ${\displaystyle o_{}}$ ${\$\$v_{o}}$은(는) 다음과 같이 앰프 내부의 이상적인 op 앰프의 이득에 의해 결정된다$$.

${\displaystyle \ v_{o}=A_{v}v_{i}\ .}$

이 관계를 사용하여 Kirchhoff의 현재 법칙을 회로 출력 측에 적용하면 다음과 같이 이상적인 op 앰프에 대한 입력에서$$ ${\displaystyle {전압}_{}}$ v ${{\$ v_${{i}$의 함수로서$$ 로드 $전압{\displaystyle {}_{}}$ v ${\$$v_$${}}$을 결정한다.

${\displaystyle {\frac {v_{\ell}}{v_{i}}=A_{v}{\frac {R_{L}{R_+R}}\,\!}$${\displaystyle \cdot{1+j\오메가 C_{C}R_{o}/A_{v}}{1+j\오메가(C_{L}+C})(R_{o}\ R_{L}}}}}}}}\ .}$

이 표현식은 회로의 입력 측에서 전체 이득을 얻기 위해 앞에서 찾은 게인수와 조합된다.

${\displaystyle {\frac {v_{\ell}}{v_{a}}={\frac {v_{v_{i}}{\frac {v_{i}}}{v_{a}}}}}}}$

${\displaystyle =A_{v}{\frac {R_{i}}{R_{i}}+R_{{{R}}}A}}\cdot {\frac {R_{L}{R_{L}+R_{O}}\,\!}$${\displaystyle \cdot {\frac {1}{1+j\omega(C_{M}+C_{i})(R_{A}\ R_{i}}}}}}\,\!}$${\displaystyle \cdot{1+j\오메가 C_{C}R_{o}/A_{v}}{1+j\오메가(C_{L}+C})(R_{o}\ R_{L}}}}}}}}\ .}$

이 이득식은 두 개의 시간 상수를 가진 단순한 2극 반응을 보여주는 것으로 보인다.(이것은 또한 분자에 0을 나타내지만, 증폭기 이득 A가_v 크다고 가정할 때, 이 0은 너무 높은 주파수에서만 중요하므로, 분자는 통일로 근사치를 구할 수 있다.)그러나 앰프에는 2극 동작이 있지만 밀러 캐패시턴스에는 낮은 주파수에서는 중요성이 없지만 높은 주파수에서는 상당한 효과가 있는 매립 주파수 의존성이 있기 때문에 위의 표현보다 두 시간 정수가 더 복잡하다.즉, 출력 R-C 제품인 C_L(R_o R_L )가 저주파극보다 훨씬 높은 주파수에 해당한다고 가정하면 밀러 근사치보다는 밀러 캐패시턴스의 정확한 형태를 사용해야 한다.밀러 효과에 관한 기사에 따르면 밀러 캐패시턴스는 다음과 같이 주어진다.

${\displaystyle {\reasoned}C_{M}&=C_{C}\왼쪽(1-{\frac {v_{\ell}}}{v_{i}}\오른쪽)\\&=C_{C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\ R_{L})}}\right)\ .\\end{aigned}}$

(양성 밀러 캐패시턴스의 경우 A는_v 음수)이 결과를 이득표현과 수집용어로 대체하면 이득은 다음과 같이 다시 쓰여진다.

${\displaystyle {\frac {v_{\ell }{v_{a}}=A_{v}{\frac {R_{i}}{R_{i}}}+R_{{{}}}}{\fracA}}{{\frac{R_{L}}{R_{L}+R_{O}}{\frac {1+j\omega C_{C_{O}/{V}}{D_{\omega }}\}}},}$

2차 Ω으로 D를_ω 부여한 경우, 즉:

${\displaystyle D_{\omega}\,\!}$ ${\displaystyle =[1+j\omega(C_{L}+C_{C})(R_{o}\ R_{L})\,\!}$ ${\displaystyle \cdot \[1+j\omega C_{i}(R_{A}\R_{i})\,\!}$ ${\displaystyle \ +j\omega C_{C}(R_{A}\ R_{i}\,\!}$ ${\displaystyle \cdot \left(1-A_{v}{\frac {R_{L}}+R_{O}}\,\!}$ ${\displaystyle \ +(j\omega )^{2}C_{C}C_{L}(R_{A}\ R_{I})(R_{O}\ R_{L}\ .}$

모든 이차성에는 두 가지 요소가 있는데, 이 표현을 그대로 다시 쓰면 더 간단해 보인다.

${\displaystyle \D_{\omega }=(1+j\\omega {\tau }_{1})(1+j\omega {\tau }_{2})$

${\displaystyle =1+j\omega({\tau }_{1}+{\tau }_{2})+(j\omega )^{2}\tau _{1}\}$

여기서 $\tau {\displaystyle {}_{}}$ ${\$1} 및 $and$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$2}}은$$D 공식의_ω 캐패시턴스와 저항의 조합이다$$.^[6]그것들은 증폭기의 두 극의 시간 상수에 해당한다.하나 또는 상수가 가장 길다 다른 시간;τ 1{\displaystyle \tau_{1}}가장 긴 시간 지속적이고 가장 낮은 기둥에 해당하는, τ 1{\displaystyle \tau_{1}}을 가정해<>τ 2{\displaystyle \tau_{2}}.( 좋은 계단 응답 을 τ 1{\displaystyle \tau_{1}}을 필요로 한다. 가정합니다. τ 2${\displaystyle \tau_{2$ 아래 C 선택을_C 참조하십시오.)

이 증폭기의 가장 낮은 극 부근에 있는 저주파에서는 일반적으로 Ω의 선형 항이 2차 항보다 중요하므로 D의_ω 저주파 동작은 다음과 같다.

${\displaystyle {\begin{aligned}\ D_{\omega }&=1+j\omega [(C_{M}+C_{i})(R_{A}\ R_{i})+(C_{L}+C_{C})(R_{o}\ R_{L})]\\&=1+j\omega (\tau _{1}+\tau _{2})\approx 1+j\omega \tau _{1}\ ,\ \\\end{aligned}}}$

여기서 C는_M 밀러 근사치를 사용하여 다음과 같이 다시 정의된다.

${\displaystyle C_{M}=C_{C}\좌측(1-A_{v}{\frac {R_{L}}{R_{L}+R}}\,},}$

그것은 단순히 낮은 주파수에서 평가된 이전의 밀러 캐패시턴스다.${\displaystyle {이\mathrm{}}_{}}$ 기준으로 {$$1{\$displaystyle \tau_{1}{$1}가 결정된다$$.$$$$$\tau {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$$tau_$${$$1}{$$1}.$ C가_M 크기 때문에 ${\displaystyle {\mathrm{}}_{}}$ 상수 constant 1${\$는 원래 값인_i C(R_Ai)^[7]보다 훨씬 크다$$.

고주파에서는 2차 항이 중요해진다.$\tau {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$}에$$대한 위의 결과가 유효하다고$$ 가정하면, 두 번째 상수인 고주파극의 위치는 D의_ω 2차 항에서 다음과 같이 발견된다.

${\displaystyle \tau_{2}={\frac {\tau_{1}{1}\tau_{1}}}\preck {\tau_{1}{1}}\pau_{1}{1}+\tau_{2}}\}\}\}\}\}\}\}\}\}}}}\$

이 표현식에서 product ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ 제품에 해당하는 2차 계수를 ${\displaystyle {1\mathrm{}}_{}}$ 1${\$에 대한 추정치와 함께$$ 대체하면 두 번째 극의 위치에 대한 추정치가 다음과 같다.

${\displaystyle {\begin{aligned}\tau _{2}&={\frac {(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\ R_{i})(R_{O}\ R_{L})}{(C_{M}+C_{i})(R_{A}\ R_{i})+(C_{L}+C_{C})(R_{o}\ R_{L})}}\\&\approx {\frac {C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C}}{C_{M}}}(R_{O}\ R_{L})\ ,\\\end{aligned}}}$

그리고 C가_M 크기 때문에 $\tau {\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$는 원래 값 C_L(R_oL R )보다 크기가 줄어든 것 같다. 즉, 높은 극은 C 때문에_C 여전히 더 높은 빈도로 이동했다.^[8]

요컨대 콘덴서 C의_C 도입으로 저극이 더 낮고 고극이 더 높게 이동하였기 때문에 극분할이라는 용어가 잘 설명되어 있는 것 같다.

C의_C 선정

C에게_C 좋은 선택은 어떤 가치인가?일반적인 용도의 경우, 전통적인 설계(흔히 지배극 또는 단극 보상이라고 함)에서는 증폭기 게인이 코너 주파수에서 20 dB/decade에서 0 dB 게인 또는 더 낮은 값으로 떨어질 것을 요구한다.^[9][10] 이 설계로 앰프는 안정적이고 유니티 게인 전압 버퍼로서도 거의 최적인 스텝 응답을 갖는다.보다 공격적인 기법은 2극 보상이다.^[11][12]

설계를 얻기 위해 f를₂ 위치시키는 방법은 그림 3과 같다.가장 낮은 극 f에서₁ 보드 이득 플롯은 20 dB/decade에서 하강하기 위해 기울기를 깨뜨린다.목표는 20 dB/decade 기울기를 0 dB까지 유지하는 것이며, (log₁₀ f₂ - log₁₀ f₁ ) = log₁₀ (f₂₂ / f₁ )의 요구되는 주파수 변화에^[13] 대해 20 로그_10v A의 원하는 이득 감소(dB in dB)의 비율을 취하는₁ 것이다.

주파수 10년당 기울기 = ${\displaystyle 20}$ ${\displaystyle l\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\mathrm{o}}{}}$ ${\displaystyle \frac{{\mathrm{}}_{}}{}}$ ${\displaystyle \frac{{\mathrm{}}_{}}{}}$ (${\displaystyle \frac{{}_{}}{}}$ v${\displaystyle \frac{{}_{}}{}}$) ${\displaystyle \frac{\mathrm{o}}{}}$ ${\displaystyle \frac{{10}_{}}{}}$(${\displaystyle \frac{{}_{}}{{f\mathrm{}}_{}}}$ 2${\displaystyle \frac{{}_{}}{}}$/ f ${\displaystyle \frac{{1\mathrm{}}_{}}{}}$)${\displaystyle \frac{}{}}$, ${\displaystyle=20{\frac {\mathrm {log_{10}(A_{v})}{\mathrm {log_{10}}}{{2$}/f_${1}}}}}\},},}$

즉, f₂ = A f_v1. f가 이만큼 크지 않을₂ 경우, 두 번째 극에서 발생하는 보드 플롯의 두 번째 파단은 결과적으로 낮은 안정성과 저하된 스텝 응답으로 이득이 0dB로 떨어지기 전에 플롯을 중단한다.

그림 3은 주파수에 대한 정확한 게인 의존도를 얻기 위해 두 번째 극은 적어도 첫 번째 극보다 주파수 A가_v 더 높은 요인임을 보여준다.게인은 앰프의 입력과 출력에서 전압 분배기에 의해 약간 감소하므로 입력과 출력에서 전압 분배기에 대한 A에_v 대한 보정으로 양호한 스텝 응답을 위한 폴 비율 조건이 다음과 같이 된다.

${\displaystyle {\frac {\tau _{1}:{1}{1}\tau _{2}}}\관련 A_{v}{\frac {R_{i}}}{R_{i}}+R_{{{}}}}}}}{\frac}}}}}}{{{{}}}}}}}}}}}}}A}}\cdot {\frac {R_{L}{R_{L}+R_{O}}\,}$

위에서 개발된 시간 상수에 대한 근사를 사용하여,

${\displaystyle {\frac {\tau _{1}{\tau _{2}}:00}\frac {(\tau _{1}+\tau _{2})^{2}}:{{1}{1}\cau _{{R_{i+}}}R_{{{R_{}}}R}R}R}R}R}R}R_A}}\cdot {\frac {R_{L}{R_{L}+R_{O}}\,}$

또는

${\displaystyle {\frac {[(C_{M}+C_{i})(R_{A}\ R_{i})+(C_{L}+C_{C})(R_{o}\ R_{L})]^{2}}{(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\ R_{i})(R_{O}\ R_{L})}}\,\!}$ ${\displaystyle {\cdot {\White}\cdot }=A_{v}{\frac {R_{i}}{R_{i}}+R_{{{R_}}}}{{{R_}}}}}}}}{{}}}}}}}A}}\cdot {\frac {R_{L}{R_{L}+R_{O}}\,}$

C에_C 대한 적절한 값을 결정하기 위한 2차 방정식을 제공한다.그림 4는 이 방정식을 사용한 예를 보여준다.이득의 낮은 값에서 이 예제를 증폭기 보상(, 그림 4보상 콘덴서 CC저 이득에 작은 거에요)도 없는 고위험이 증가하면 보상 용량은 급속히가 필요한(그림 4에서 증가한 capacitor CC가 증가함에 따라 신속하게 그것은, 보상이)기 때문에 neces은 pole-ratio 조건에 맞다.s장대비가 증가하다여전히 더 큰 이득의 경우, 이득에 따라 증가하는 C의_C 밀러 증폭("밀러 방정식" 참조)이 C에_C 대해_C 더 작은 값을 허용하기 때문에 필요한 C는 이득과 함께 떨어진다.

설계 불확실성에 대한 더 많은 안전 여유를 제공하기 위해, 종종 A는_v 이 방정식의 오른쪽에서 두 배 또는_v 세 배 A로 증가한다.^[14]산센^[4] 또는 후이징^[10] 및 단계별 응답에 대한 기사를 참조하십시오.

슬루 레이트

위의 내용은 작은 신호 분석이다.그러나 큰 신호를 사용할 경우 보정 캐패시터를 충전 및 방전해야 하는 필요성이 앰프 슬루 레이트에 악영향을 미치며, 특히 입력 램프 신호에 대한 응답은 C 충전_C 필요성에 의해 제한된다.

참고 항목

• 주파수 보상
• 밀러 효과
• 공통출처
• 복음도
• 스텝 응답
• CMOS 증폭기

참조 및 참고 사항

외부 링크

• 회로 이론 위키북의 보드 플롯
• 제어 시스템 위키북의 보드 플롯