밀러 정리

밀러 정리는 등가 회로를 만드는 과정을 말한다.직렬로 연결된 두 개의 전압 소스에 의해 공급되는 부동 임피던스 소자는 해당 임피던스가 있는 두 개의 접지된 소자로 분할될 수 있다고 주장한다.병렬로 연결된 두 개의 전류 공급원에 의해 공급되는 임피던스에 관한 이중 밀러 정리도 있다.두 버전은 두 Kirchhoff의 회로법에 근거한다.

밀러 이론은 순수한 수학적인 표현만이 아니다.이러한 배열은 임피던스(Miller effect, 가상 접지, 부트스트래핑, 음극 임피던스 등)의 수정에 관한 중요한 회로 현상을 설명하고 다양한 공통 회로(피드백 증폭기, 저항성 및 시간 의존성 컨버터, 음극 임피던스 컨버터 등)의 설계와 이해를 돕는다.이 이론들은 '회로 분석'에서 특히 높은^[1] 주파수에서 피드백과 특정 트랜지스터 증폭기로 회로를 분석하는 데 유용하다.^[2]

밀러 정리와 밀러 효과 사이에는 밀접한 관계가 있다: 정리는 효과의 일반화로 간주될 수 있고 그 효과는 정리의 특별한 경우로서 생각될 수 있다.

밀러 정리(전압용)

정의

Miller 정리는 선형 회로에 임피던스 $Z$ $Z$ 의 분기가 있고 $Z$ 노달 $V_{1}$ V 1 $V_{1}$ {\ $displaystyle V_{1$ } $V_{2}$ V $V_{2}$ ${\$ }}개의 노드를 연결하는 경우 임피던스에 의해 해당 노드를 지면에 연결하는 두 개의 분기로 이 분기를 교체할 수 있다는 것을 확립한다 $V_{2}$ 각각 ${\frac {Z}{1-K}}$ ${\frac {Z}{1-K}}$ - ${\frac {Z}{1-K}}$ ${\$ 및 ${\frac {Z}{1-K}}$ ${\frac {KZ}{K-1}}$ ${\frac {KZ}{K-1}}$ ${\frac {KZ}{K-1}}$ - 1 ${\$ {\ $frac{KZ}{K-1$ $K={\frac {V_{2}}{V_{1}}}$ 서 K $K={\frac {V_{2}}{V_{1}}}$ = $K={\frac {V_{2}}{V_{1}}}$ $K={\frac {V_{2}}{V_{1}}}$ $K={\frac {V_{2}}{V_{1}}}$ 1 ${\$ }:{ $V_{1$ }:{1 $K={\frac {V_{2}}{V_{1}}}$ 밀러 정리는 등가 2포트 네트워크 기법을 사용하여 등가 2포트 네트워크 기법을 동등한 것으로 대체하고 소스 흡수 정리를 적용함으로써 증명될 수 있다.^[3]이 버전의 밀러 정리는 키르흐호프의 전압 법칙에 근거하고 있다. 그러한 이유로 전압에 대해서도 밀러 정리로 명명된다.

설명

밀러의 정리에 대한 도식.

밀러 정리는 임피던스 소자가 공통 접지를 통해 직렬로 연결된 두 개의 임의(필수 종속적이지 않은) 전압 선원에 의해 공급된다는 것을 암시한다.실제로 이들 중 하나는 전압 $V_{1}$ $V_{1}$ ${\$ }의 주(독립) 전압 소스로, 다른 $V_{1}$ 하나는 전압 V $V_{2}=K{V_{1}}$ = K $V_{2}=K{V_{1}}$ $V_{2}=K{V_{1}}$ ${\$ 의 추가(선형 종속) 전압 소스로서 작용한다 $V_{2}=K{V_{1}}$ Miller 정리(입출력원의 측면에서 보이는 회로 임피던스 수정)의 아이디어는 추가 전압 $V_{2}$ $V_{2}$ 2 ${\$ }를 사용하지 않은 경우와 연결하지 않은 경우를 비교함으로써 아래와 같다 $V_{2}$

$V_{2}$ $V_{2}$ ${\$ }}이 $V_{2}$ 0이면( $임피던스$ Z ${\displaystyle$ Z $}$ 이(가) 방금 접지된 $Z$ 두 번째 전압 소스가 없거나 소자의 오른쪽 끝이 접지된 경우), 옴의 법칙에 따라 소자를 통과하는 입력 전류가 결정되며, V $V_{1}$ ${\$ }에 의해서만 결정된다.

I_{in0}={\frac {V_{1}{Z}}

회로의 입력 임피던스는

Z_{in0}={\frac {V_{1}:{1}{{}}}{\fracI_{in0}}}=Z.

두 번째 전압 소스가 포함되면 입력 전류는 두 전압에 따라 달라진다. $V_{2}$ 에 따라 $V_{2}$ 2 ${\$ }}개를 $V_{2}$ $V_{1}$ $V_{1}$ ${\$ }에서 빼거나 더하기 때문에 입력 전류가 감소/증가한다 $V_{1}$

I_{in}={\frac {V_{1}-V_{2}}:{Z}}{\frac {(1-K)}{Z}{V_{1}={(1-K)}}}}{I_{in0}}

입력 소스의 측면에서 볼 수 있는 회로의 입력 임피던스가 증가/감소됨

Z_{in}={\frac {V_{1}:{1}{{}}}{\fracI_{in}}={\frac {Z}{1-K}}}

따라서 밀러 정리는 입력 전압 소스와 직렬로 $V_{2}=K{V_{1}}$ 두 번째 전압 소스와 비례 전압 $V_{2}=K{V_{1}}$ 2 $V_{2}=K{V_{1}}$ = K $V_{2}=K{V_{1}}$ $V_{2}=K{V_{1}}$ ${\$ 을(를) 연결하면 입력 소스 측면에서 보이는 회로 임피던스, 즉 유효 전압, 전류 및 회로 임피던스가 각각 변경된다는 사실을 표현한다.극성에 따라 $V_{2}$ $V_{2}$ ${\$ }}는 임피던스를 통해 전류를 통과시키기 위해 주 전압원을 돕거나 반대하여 보조 전압원으로 작용한다 $V_{2}$ .

두 전압 소스의 조합을 새로운 합성 전압 소스로 제시함으로써 이외에도 실제 소자와 두 번째 전압 소스를 동적으로 변형된 임피던스를 가진 새로운 가상 소자로 결합함으로써 정리를 설명할 수 있다.이러한 관점에서 $V_{2}$ $V_{2}$ ${\$ }}은 $임피던스$ Z $Z$ 에서 $V_z$ 전압 강하 $V_{z}$ z ${\$ 를 인위적으로 증가/감소하여 $Z$ 전류를 감소/증가시키는 추가 전압이다 $V_{2}$ .전압 사이의 비율은 획득한 임피던스의 값을 결정하며(아래 표 참조) 총 6개의 일반적인 애플리케이션 그룹을 제공한다.

**$V_{1}$ $V_{1}$ ${\$ }에서 $V_{2}$ $V_{2}$ $V_{2}$ ${\$ ${$ $1}$ 빼기**
$V_{2}$ $V_{2}$ ${\$ }} 대 $V_{2}$ $V_{1}$ $V_{1}$ ${\$ }	$V_{2}=0$	${\displaystyle 0<V_{2}<V_{1}.$	$V_{2}=V_{1}:{1$	$V_{2}>V_{1}:{1$
임피던스	정상의	증가된	무한의	전류 역전 시 음의

**$V_{1}$ $V_{1}$ 에 $V_{2}$ $V_{2}$ ${\$ } 추가**
$V_{2}$ $V_{z}$ $V_{2}$ ${\$ 대 $V_{2}$ $V_{z}$ z ${\$	$V_{2}=0$	$0<V_{2}<V_{z}$	$V_{2}=V_{z}}$	$V_{2}>V_{z}$
임피던스	정상의	줄었다	영	전압 반전 시 음극

전압 $V_{1}$ $V_{1}$ ${\$ 및 $V_{1}$ $V_{2}$ 2 ${\$ 2}}: 전압이 $V_{2}$ $K$ 과 계수 K {\ $displaystyle K}$ 을(를 $)$ $1K$ {\displaystyle ${\frac{1}{K$ }}로 대체하는 $K$ 경우 출력 소스 측면에서 볼 수 있는 회로 임피던스를 유사하게 정의할 수 있다.

Z_{in2}={\frac {{K}{Z}}{K-1}}

실행

싱글 엔드 전압 증폭기에 기초한 밀러 정리의 일반적인 구현

가장 자주,^[2] 밀러 정리는 접지된 일반 선형 네트워크의 두 단자 사이에 연결된 $Z$ $임피던스$ Z ${\displaystyle$ Z $}$ 을(를) 가진 소자로 구성된 배열에서 관찰되고 구현될 수 있다.보통 $A_{V}=K$ $A_{V}=K$ = $A_{V}=K$ $A_{V}=K$ 의 이득이 있는 전압 증폭기는 이와 같은 선형 네트워크 역할을 하지만 $A_{V}=K$ 다른 장치도 이러한 역할을 수행할 수 있다. 즉 전위차계의 null-balance 미터에 있는 인간과 전위차계, 전자기계 통합자(전위차 피드백 센서를 사용한 서보마이즘) 등이 그것이다.

앰프 구현 시 입력 전압 V $V_{i}$ ${\$ 는 $V_{i}$ $V_{1}$ $V_{1}$ 1 $V_{1}$ {\ $displaystyle V_{1}:{$ $o}$ 은(는 $)$ V $V_{o}$ $V_{2}$ ${\$ 입력 전압 소스에는 내부 임피던스 $Z_{int}$ $Z_{int}$ t ${\$ 이 있는 경우가 많다. $Z_{int}$ $또는$ Z $Z$ 과 $Z$ 와) 조합하여 피드백을 도입하는 추가 입력 임피던스가 연결된다.증폭기의 종류(비인버팅, 반전 또는 미분)에 따라 피드백은 양, 음 또는 혼합될 수 있다.

밀러 앰프 배치는 두 가지 측면을 가진다.

앰프는 실제 임피던스를 가상 임피던스로 변환하는 추가 전압 소스로 생각할 수 있다(앰프는 실제 요소의 임피던스를 수정한다).
가상 임피던스는 앰프 입력에 병렬로 연결된 소자로 생각할 수 있다(가상 임피던스는 앰프 입력 임피던스를 수정한다).

적용들

앰프 입력과 출력 포트를 연결하는 임피던스의 도입은 분석 과정에 많은 복잡성을 더한다.밀러 정리는 특히 피드백을^[2] 통해 일부 회로의 복잡성을 줄이는 데 도움이 된다.그러나 밀러 정리는 등가 회로를 만드는 데 효과적인 도구일 뿐만 아니라 임피던스를 추가 전압에 의해 수정하는 것에 기초하여 회로를 설계하고 이해하는 강력한 도구다.출력 전압 대 입력 전압의 극성 및 그 크기 사이의 비율에 따라 6개의 일반적인 상황 그룹이 있다.그 중 일부에서 밀러 현상은 의도하지 않은 (부스트스트래핑) 또는 원하지 않는 (밀러 효과)로 나타나며, 다른 경우에는 의도적으로 도입된다.

$V_{1}$ $V_{1}$ ${\$ }에서 $V_{2}$ $V_{2}$ $V_{2}$ ${\$ }를 뺀 애플리케이션

이러한 애플리케이션에서는 루프를 따라 이동하는 $V_{i}$ 입력 전압 $V_{i}$ $V_{i}$ ${\$ $displaystyle V_{$ $i$ }에 대해 출력 전압 $V_{o}$ $V_{o}$ ${\$ $displaystyle V_{i}}$ 이(가) 반대 극성으로 삽입된다 $V_{o}$ .그 결과, 임피던스를 통과하는 유효 전압과 전류를 통해 임피던스가 감소하고, 입력 임피던스가 증가한다.

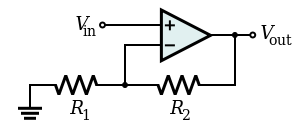
증가된 임피던스는 게인 $0<A_{v}<1$ < $0<A_{v}<1$ < $0<A_{v}<1$ > $0<A_{v}<1$ 의 게인(gain)이 없는 증폭기에 의해 구현된다 $0<A_{v}<1$ 출력 전압(규모)이 입력 전압 $V_{i}$ $V_{i}$ ${\$ 보다 작으며 부분적으로 $V_{i}$ 중화시킨다.입력 임피던스가 적당히 증가하는 직렬 음극 피드백(이메터, 소스, 음극 팔로워 등)을 가진 불완전한 전압 팔로워와 증폭기(이메터 퇴화)가 그 예다.

op-amp 비인버팅 앰프는 밀러 정리에 기초한 직렬 음극 피드백을 가진 일반적인 회로로, op-amp 차동 입력 임피던스가 명백히 무한대로 증가된다.

무한 임피던스는 $A_{v}=1$ $A_{v}=1$ = $A_{v}=1$ ${\displaystyle A_{v}=1$ }이 $A_{v}=1$ 가) 있는 비인버팅 앰프를 사용한다.출력 전압은 입력 전압 $V_{i}$ $V_{i}$ ${\$ 와 동일하며 $V_{i}$ 완전히 중화시킨다.회로 입력 임피던스가 엄청나게 증가하는 직렬 음극 피드백(op-amp follower 및 비인버팅 앰프)이 있는 전위차계 null-balance meter와 op-amp 팔로워 및 증폭기가 그 예다.이 기법은 부트스트래핑이라고 하며, 회로,^[4] 입력 보호 회로 등에 의도적으로 사용된다.

전류 역전으로 얻은 음의 임피던스는 $A_{v}>1$ $A_{v}>1$ > $A_{v}>1$ $[\displaystyle A_{v}]1}$ 을(를) 가진 비반복 증폭기에 의해 구현된다 $A_{v}>1$ 출력 전압이 입력 전압보다 높기 때문에 전류가 방향을 바꾼다.입력 전압 소스에 내부 임피던스 $Z_{int}$ $Z_{int}$ $Z_{int}$ ${\$ 이(가) 있거나 $Z_{int}$ 다른 임피던스 소자를 통해 연결된 경우 양의 피드백이 나타난다.대표적인 어플리케이션은 음과 양의 피드백을 모두 사용하는 전류 반전(INIC)이 있는 음의 임피던스 컨버터(음의 피드백은 비삽입 증폭기와 양의 피드백 - 임피던스를 수정하는 데 사용된다)이다.

$V_{1}$ $V_{1}$ {\displaystyle $V_$ {1}에 $V_{2}$ V 2 ${\$ }를 $V_{2}$ 추가하는 데 기반한 애플리케이션

이러한 응용 프로그램에서는 루프를 따라 $V_{i}$ 이동하는 입력 $V_{i}$ $V_{i}$ i $V_{i}$ {\ $displaystyle V_$ {i $}$ 에 대해 출력 $V_{o}$ V $V_{o}$ {\ $displaystyle V_{i$ $}}$ 이(가) 동일한 극성으로 삽입된다 $V_{o}$ . 결과적으로 임피던스를 통한 유효 전압과 전류가 증가하며 입력 임피던스가 감소한다.

임피던스 감소는 보통 $10<A_{v}<1000$ < $10<A_{v}<1000$ < $>[\displaystyle 10 <A_{v}<1000}$ .유효 입력 캐패시턴스가 증가하는 공통 입출력, 공통 소스 및 공통 카테터 증폭 단계에서 원하지 않는 밀러 효과로 관찰될 수 있다.범용 작동 증폭기 및 트랜지스터 밀러 통합기에 대한 주파수 보상은 밀러 효과의 유용한 사용 예다.

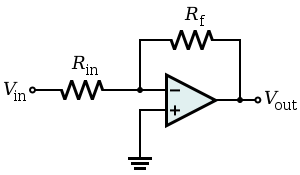
Op-amp 인버팅 앰프는 Miller 정리를 기반으로 병렬 음극 피드백을 갖는 대표적인 회로로, 여기서 Op-amp 차동 입력 임피던스는 명백히 0까지 감소한다.

영점 임피던스는 게인 $A_{v}\to \infty$ v $A_{v}\to \infty$ → $∞[\$ displaystyle $A_{v}\to \ft$ }}}을 $($ 를) 엄청나게 높은 게인 A $A_{v}\to \infty$ → \ $displaystyle$ A_ ${v$ }\ $to$ \ft}}}을(를) 가진 인버팅(일반적으로 op-amp) 앰프를 사용한다 $A_{v}\to \infty$ 출력 전압은 임피던스에서 $V_{z}$ $V_{z}$ V z ${\{$ z $}$ 와 거의 동일하고 완전히 중화시킨다.회로는 짧은 연결로 동작하며 입력에 가상 접지가 나타나므로 정전압 소스에 의해 구동되어서는 안 된다.이를 위해 일부 회로는 정전류 소스 또는 내부 임피던스를 가진 실제 전압 소스(전류 대 전압 변환기(트랜시펜스 앰프), 용량성 통합기(이름 또한 전류 통합기 또는 차지 앰프), 저항 대 전압 변환기(임피던스 위치에 연결된 저항성 센서)에 의해 구동된다. $Z$ $Z$ $Z$ .

나머지는 입력에 직렬로 연결된 추가 임피던스(전류 증폭기), 반전 증폭기, SUM 증폭기, 유도 통합기, 용량성 차별화기, 저항 용량성 통합기, 용량성 차별화기, 유도 저항성 차별화기, 유도 저항성 차별화기 등이다.이 목록에서 변환하는 통합자들은 밀러 효과의 극단적 표현에서 유용하고 원하는 적용의 예들이다.

병렬 음극 피드백이 있는 이러한 모든 Op-amp 인버팅 회로에서 입력 전류가 최대값으로 증가한다.옴의 법칙에 따라 입력 전압과 입력 임피던스에 의해서만 결정되며 임피던스 $Z$ ${\displaystyle$ Z $}$ 에 의존하지 않는다 $Z$

전압 역전이 있는 음극 임피던스는 차동 입력이 있는 오펜스 앰프에 음극 및 양의 피드백을 모두 적용하여 구현한다.입력 전압 소스는 $Z_{int}>0$ 임피던스 $Z_{int}>0$ $Z_{int}>0$ $Z_{int}>0$ > 0 $Z_{int}>0$ 을(를) 가지거나 $Z_{int}>0$ 다른 임피던스 요소를 통해 입력에 연결해야 한다.이러한 조건 하에서 회로의 $V_{i}$ 입력 $V_{i}$ V $V_{i}$ {\ $displaystyle V_{$ $i}$ 는 출력 전압이 임피던스 $V_{z}$ $V_{i}=V_{z}-V_{o}<0$ $V_{i}=V_{z}-V_{o}<0$ V $V_{i}=V_{z}-V_{o}<0$ - $V_{i}=V_{z}-V_{o}<0$ V $V_{i}=V_{z}-V_{o}<0$ < 0>{\ $displaystyle V_{i}=V_{z}-V_{$ $o$ }< $0})$ 를 초과함에 따라 극성이 변경된다.

대표적인 용도는 전압 반전(VNIC)이 있는 음극 임피던스 컨버터다.^[5]회로 입력 전압이 출력 전압과 동일한 극성을 가지지만, 인버팅 op-amp 입력에 적용된다는 점이 흥미롭다. 입력 소스는 회로 입력 및 출력 전압과 모두 정반대의 극성을 갖는다.

밀러 배열의 일반화

원래의 밀러 효과는 두 노드 사이에 연결된 용량성 임피던스에 의해 구현된다.밀러 정리는 노드 사이에 연결된 $Z$ 임의의 $임피던스$ Z ${\displaystyle$ Z $}$ 을 암시하므로 밀러 효과를 일반화한다.또한 상수 계수 $K$ $K$ 을(를) 사용해야 하며 $K$ 그러면 위의 식이 유효하다.그러나 이러한 요건이 위반되고 임피던스와 계수를 동력화하여 이 배열을 더욱 일반화할 수 있는 경우에도 밀러 정리의 수정 성질이 존재한다.

비선형 원소.임피던스 외에도 밀러 배열은 임의 원소의 IV 특성을 수정할 수 있다.다이오드 로그 변환기의 회로는 다이오드의 로그 전진 IV 곡선이 $y$ $y$ 축과 $y$ 겹치는 수직 직선으로 변환되는 비선형 가상 영점 저항의 예다.

일정하지 않은 계수.계수 $K$ $K$ 이(가) 변하면 $K$ 이국적인 가상 요소를 얻을 수 있다.집광기 회로는 인덕턴스, 캐패시턴스 또는 반전된 저항을 모방하도록 저항 R $R_{L}$ ${\$ 을 $R_{L}$ 수정한 가상 요소의 예다.

듀얼 밀러 정리(전류)

정의

또한 Kirchhoff의 현재 법칙(전류의 밀러 정리): $임피던스$ Z $Z$ 를 $Z$ 연결한 회로에 두 개의 $I_{1}$ I 1 ${\$ }와 $I_{1}$ I $I_{2}$ ${\$ }}가 접지로 수렴하는 $I_{2}$ 분기가 있으면 t를 대체할 수 있다.his branch by two conducting the referred currents, with imperespectively equal to $(1+\alpha )Z$ and ${\frac {(1+\alpha )Z}{\alpha }}$ , where ${\displaystyle \alpha ={\frac {I_{2}}{$ $I_{1}:{$ 1 $\alpha ={\frac {I_{2}}{I_{1}}}$ 이중 정리는 2포트 네트워크를 동등한 것으로 교체하고 소스 흡수 정리를 적용함으로써 증명될 수 있다.^[3]

설명

듀얼 밀러 정리는 실제로 비례 전류 $I_{2}=KI_{1}$ 2 $I_{2}=KI_{1}$ = $I_{2}=KI_{1}$ $I_{2}=KI_{1}$ $I_{2}=KI_{1}$ ${\$ }를 주 입력 소스와 병렬로 연결하고 $I_{2}=KI_{1}$ 임피던스 소자가 이를 통과하는 전류, 전압 및 그에 따라 측면에서 보이는 회로 임피던스를 변화시킨다는 사실을 표현한다.입력 소스의방향에 따라 $I_{2}$ $I_{2}$ ${\$ }}은 임피던스 전체에 걸쳐 전압을 생성하기 위해 $I_{1}$ 주 전류 소스 $I_{1}$ ${\$ }에 도움이 되거나 반대되는 보조 전류 소스 역할을 한다 $I_{2}$ .실제 소스와 두 번째 전류 소스의 조합은 동적으로 수정된 임피던스를 가진 새로운 가상 소자로 생각할 수 있다.

실행

이중 밀러 정리는 일반적으로 부동 임피던스를 통해 $Z$ 접지 임피던스 $Z$ ${\displaystyle$ Z $}$ 을(를) 공급하는 두 개의 전압 소스로 구성된 배열에 의해 구현된다(그림 3 참조).전압 소스와 해당 임피던스의 조합은 두 개의 전류 소스, 즉 주 전원과 보조 전류를 형성한다.주 밀러 정리의 경우와 마찬가지로 보통 두 번째 전압은 전압 증폭기에 의해 생성된다.증폭기의 종류(인버팅, 비인버팅 또는 차등)와 게인에 따라 회로 입력 임피던스가 사실상 증가, 무한, 감소, 0 또는 음의 증가가 있을 수 있다.

적용들

주 밀러 정리로서 회로 분석 과정을 돕는 것 외에도 듀얼 버전은 추가 전류에 의한 임피던스 수정을 기반으로 한 회로를 설계하고 이해하는 강력한 도구다.대표적인 용도는 부하 취소기,^[6] 캐패시턴스 중화제,^[7] 하울랜드 전류원 및 그 파생 모델인 데부 통합자로서 음의 임피던스를 가진 일부 이국적인 회로들이다.^[8]마지막 예(여기 그림 1 참조), 하우랜드 전류 소스는 입력 전압 소스 $V_{in}$ i $V_{in}$ ${\$ 양의 저항 $R$ ${\displaystyle R},$ 로드 $R$ 임피던스 $Z$ ${\displaysty$ Z $} 역할$ 을 하는 콘덴서 $C$ $C$ ${\displaysty C$ $Z$ 음의 임피던스 변환기( $R_{1}=R_{2}=R_{3}=R$ 1 $R_{1}=R_{2}=R_{3}=R$ 로 구성된다. $R_{1}=R_{2}=R_{3}=R$ $R_{1}=R_{2}=R_{3}=R$ = R $R_{1}=R_{2}=R_{3}=R$ = R ${\displaystyle R_{1}=R_{2}=R_{3}=R$ 및 op-amp).입력 전압 소스와 $저항기$ R $R$ 은 부하를 통해 $I_{R}$ 전류 $I_{R}$ ${\$ 을 통과하는 불완전한 전류 소스를 구성한다 $R$ (소스 그림 3 참조).INIC는 부하를 통해 $I_{-R}$ $I_{-R}$ I $I_{-R}$ - $I_{-R}$ ${\$ 를 "도움"으로 전달하는 두 번째 전류 소스로 작용한다.그 결과 부하를 통과하는 총 전류가 일정하고 입력 소스에 의해 보이는 회로 임피던스가 증가한다.이에 비해 부하 취소기에서^{[permanent dead link]} INIC는 모든 필요한 전류를 부하를 통해 전달한다. 입력 소스의 측면에서 보이는 회로 임피던스(부하 임피던스)는 거의 무한하다.

Miller의 이론에 기초한 특정 응용 프로그램 목록

아래는 두 개의 밀러 이론에 기초한 회로 해법, 현상 및 기법의 목록이다.

회로 솔루션

전위차계 null-balance meter
전위차계 서보 시스템을 갖춘 전자기계 데이터 기록기
이미터(소스, 음극) 팔로워
이미터(소스, 음극) 변조가 있는 트랜지스터 앰프
트랜지스터 부트스트랩 바이어싱 회로
트랜지스터 통합기
공통 이미터(공통 소스, 공통 캐패시턴스)로 단계 증폭
Op-amp 팔로워
Op-amp 비인버팅 앰프
입력 임피던스가 높은 Op-amp 부트스트랩 AC 팔로워
양자 전류원
전류 역전이 있는 음극 임피던스 컨버터(INIC)
음임피던스 로드 취소기
음극 임피던스 입력 캐패시턴스 취소기
하우랜드 전류 소스
디보 통합업체
Op-amp 인버팅 전류계
Op-amp 전압 대 전류 변환기(전류 증폭기)
Op-amp 전류 대 전압 변환기(트랜스피던스 앰프)
Op-amp 저항-전류 변환기
Op-amp 저항 대 전압 변환기
Op-amp 인버팅 앰프
오프앰프 인버팅
Op-amp 역전 용량성 통합자(전류 통합자, 차지 앰프)
OP암페어 변환 저항 용량성 통합기
Op-amp 변환 용량성 차별화기
Op-amp 변환 용량성 저항성 차별화기
Op-amp 반전 유도형 집적기
Op-amp 반전 유도저항 차별화기 등
Op-amp 다이오드 로그 컨버터
Op-amp 다이오드 안티로그 컨버터
Op-amp 인버팅 다이오드 리미터(정밀 다이오드)
전압 반전(VNIC) 등이 있는 음극 임피던스 컨버터

회로현상 및 기법

부트스트래핑
고임피던스 op-amp 회로의 입력 보호
입력 캐패시턴스 중화
가상 그라운드
밀러 효과
주파수 op-amp 보상
음임피던스
부하취소

참고 항목

참조

^ "Miscellaneous network theorems". Netlecturer.com. Archived from the original on 2012-03-21. Retrieved 2013-02-03.
^ ^a ^b ^c "EEE 194RF: Miller's theorem" (PDF). Retrieved 2013-02-03.
^ ^a ^b "Miller's theorem". Paginas.fe.up.pt. Retrieved 2013-02-03.
^ 웨이백 머신 AN-241에서 고임피던스 Op Amps 아카이빙 2010-09-23 작업
^ "Nonlinear Circuit Analysis – An Introduction" (PDF). Retrieved 2013-02-03.
^ 부저항 부하 취소기가 무거운 부하를 운전하는 데 도움이 됨
^ D. H. Sheingold (1964-01-01), "Impedance and admittance transformations using operational amplifiers", The Lightning Empiricist, 12 (1), retrieved 2014-06-22
^ "Consider the "Deboo" Single-Supply Integrator". Maxim-ic.com. 2002-08-29. Retrieved 2013-02-03.

추가 읽기

Behzad Razavi의 Microelectronics 기초
아델 세드라와 케네스 스미스의 마이크로 전자회로
Jeremy Everard의 RF 회로 설계 기초

외부 링크

[1] "Miscellaneous network theorems". Netlecturer.com. Archived from the original on 2012-03-21. Retrieved 2013-02-03.

[sandiego-2] "EEE 194RF: Miller's theorem" (PDF). Retrieved 2013-02-03.

[paginas-3] "Miller's theorem". Paginas.fe.up.pt. Retrieved 2013-02-03.

[4] 웨이백 머신 AN-241에서 고임피던스 Op Amps 아카이빙 2010-09-23 작업

[5] "Nonlinear Circuit Analysis – An Introduction" (PDF). Retrieved 2013-02-03.

[load_canceller-6] 부저항 부하 취소기가 무거운 부하를 운전하는 데 도움이 됨

[7] D. H. Sheingold (1964-01-01), "Impedance and admittance transformations using operational amplifiers", The Lightning Empiricist, 12 (1), retrieved 2014-06-22

[8] "Consider the "Deboo" Single-Supply Integrator". Maxim-ic.com. 2002-08-29. Retrieved 2013-02-03.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search

밀러 정리

네임스페이스

더

목차

밀러 정리(전압용)

정의

설명

실행

적용들

$V_{1}$ $V_{1}$ ${\$ }에서 $V_{2}$ $V_{2}$ $V_{2}$ ${\$ }를 뺀 애플리케이션

$V_{1}$ $V_{1}$ {\displaystyle $V_$ {1}에 $V_{2}$ V 2 ${\$ }를 $V_{2}$ 추가하는 데 기반한 애플리케이션

밀러 배열의 일반화

듀얼 밀러 정리(전류)

정의

설명

실행

적용들

Miller의 이론에 기초한 특정 응용 프로그램 목록

참고 항목

참조

추가 읽기

외부 링크

Search

밀러 정리

밀러 정리(전압용)

정의

설명

실행

적용들

V 1 {\displaystyle V_{1}에서 V 2 {\displaystyle V_{1}를 뺀 애플리케이션

V 1 {\displaystyle V_{1}에 V 2 {\displaystyle V_{1}를 추가하는 데 기반한 애플리케이션

밀러 배열의 일반화

듀얼 밀러 정리(전류)

정의

설명

실행

적용들

Miller의 이론에 기초한 특정 응용 프로그램 목록

참고 항목

참조

추가 읽기

외부 링크

$V_{1}$ $V_{1}$ ${\$ }에서 $V_{2}$ $V_{2}$ $V_{2}$ ${\$ }를 뺀 애플리케이션

$V_{1}$ $V_{1}$ {\displaystyle $V_$ {1}에 $V_{2}$ V 2 ${\$ }를 $V_{2}$ 추가하는 데 기반한 애플리케이션