핀치(플라스마물리학)
Pinch (plasma physics)핀치(또는: 베넷 핀치[2]), 전자파 핀치,[3] 자기 핀치,[4] 핀치 효과 [5]또는 플라스마 핀치)는 자기력에 의해 전도성 필라멘트를 압축하거나, 또는 이와 같은 기능을 하는 장치를 말한다.[6]도체는 보통 플라즈마지만 고체 또는 액체 금속일 수도 있다.핀치는 통제된 핵융합 발전 실험에 사용되는 최초의 장치였다.[7]
핀치는 번개 볼트,[8] 행성 오로라,[9] 현재 시트,[10] 태양 플레어와 같은 전기 방전에서 자연적으로 발생한다.[11]
기본 메커니즘
종류들
핀치는 자연과 실험실에 존재한다.핀치는 기하학적 구조와 작동력이 다르다.[12]여기에는 다음이 포함된다.
- 제어되지 않음 – 전류가 대량으로 이동할 때마다(예: 번개, 호, 스파크, 방전) 자기력이 플라즈마를 끌어당길 수 있다.이것은 핵융합에 불충분할 수 있다.
- 시트 핀치 – 천체물리학적 효과, 이것은 방대한 양의 전하 입자로부터 발생한다.[13]
- Z-핀치 – 자기장이 방위각인 동안 실린더의 축 또는 벽을 따라 전류가 흐른다.
- 세타 핀치 – 자기장이 실린더의 축을 따라 흐르는 반면, 전기장은 방위 방향(타트론이라고도[14] 함)
- 나사 핀치 – Z-핀치와 세타 핀치의[15] 조합(안정화된 Z-핀치 또는 θ-Z 핀치라고도 함)[16][17]
- 반전된 필드 핀치 또는 토로이드 핀치 – 이것은 토러스 모양으로 배열된 Z-핀치 입니다.플라즈마는 내부 자기장을 가지고 있다.이 고리의 중심에서 거리가 증가하면 자기장이 방향을 반대로 바꾼다.
- 역 핀치 – 초기 융접 개념으로, 이 장치는 혈장으로 둘러싸인 막대로 구성되었다.전류가 플라즈마를 통과하여 중심봉을 따라 되돌아왔다.[18]이 기하학은 지휘자가 옆구리가 아닌 중앙에 있다는 점에서 z핀치와는 약간 달랐다.
- 원통 핀치
- 직교 핀치 효과
- 제품 핀치 – 바나나 궤도 내부의 입자가 응축될 때 토카막 플라즈마 내부에서 발생하는 핀치.[19][20]
- 자기화 라이너 관성 핵융합(MagLIF) – 금속 라이너 내부에 예열된, 전자기화된 연료의 Z-핀치로서, 더 큰 펄스 동력 드라이버로 점화 및 실용적 핵융합 에너지를 발생시킬 수 있다.[21]
일반적인 행동
핀치가 불안정해질 수 있다.[22]그것들은 전파, 전자파, 적외선, X선,[23] 감마선,[24] 싱크로트론 방사선,[25] 가시광선을 포함한 전체 전자기 스펙트럼에 걸쳐 에너지를 방출한다.그들은 또한 핵융합 산물로서 중성자를 생산한다.[26]
애플리케이션 및 장치
핀치는 X선을 생성하기 위해 사용되며 생성되는 강한 자기장은 금속의 전자기 형성에 사용된다.그들은 또한 입자 빔 무기,[28] 천체물리학 연구를[29] 포함한 입자 빔에[27] 응용을 하고 있으며, 우주 추진에 그것을 사용하는 것이 제안되었다.[30]퓨전 파워를 연구하기 위해 많은 대형 핀치 머신이 제작되었다. 여기 몇 가지가 있다.
- 임페리얼 칼리지의 까치 아 Z-핀치.이것은 많은 양의 전류를 전선에 투하한다.이러한 조건하에서 전선은 혈장이 되고 압축되어 핵융합을 생성한다.[31]
- 산디아 국립 연구소의 Z 펄스 전력 설비
- 영국 컬럼의 제타 장치
- 매디슨 위스콘신 대학교의 매디슨 대칭 토러스
- 이탈리아에서 역전 필드 eXperiment.
- 뉴저지 주의 촘촘한 플라즈마 초점
- 네바다 대학교 리노(미국)
- 코넬 대학교 (미국)
- 미시간 대학교 (미국)
- 캘리포니아 대학교 샌디에이고(미국)
- 워싱턴 대학교 (미국)
- 루어 대학교 (독일)
- 에콜 폴리테크니크 (프랑스)
- 바이즈만 과학 연구소(이스라엘)
- 우니베르시다드 오토노마 메트로폴리타나(멕시코).
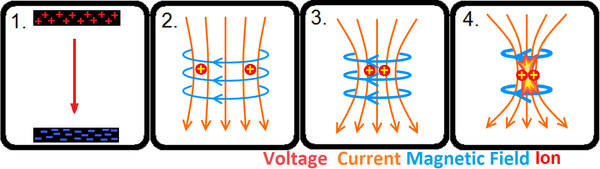
핀치 효과로 캔 파쇄
많은 고전압 전자제품 애호가들은 그들만의 조잡한 전자파 형성 장치를 만든다.[32][33][34]그들은 1차 코일의 강한 자기장에 의해 캔에 큰 전류가 유도될 때 발생하는 로렌츠 힘을 사용하여 알루미늄 청량음료통을 분쇄할 수 있는 세타 핀치를 생산하기 위해 펄스 동력 기술을 사용한다.[35][36]
전자파 알루미늄 캔 파쇄기는 전기 에너지 공급원을 제공하는 고전압 DC 전원 공급기, 전기 에너지를 축적하는 대규모 에너지 방전 캐패시터, 고전압 스위치 또는 스파크 갭, 저장되는 강력한 코일(고자압 생존 가능)의 4가지 주요 구성 요소로 구성된다.그에 상응하는 강한 핀칭 자기장을 생성하기 위해 전기 에너지를 빠르게 방출할 수 있다(아래 다이어그램 참조).
실제로 그러한 기기는 핀치를 최대화하고 기기가 안전하게 작동하도록 하기 위해 전류를 제어하는 전기 구성부품을 포함하여 도식도가 제시하는 것보다 다소 정교하다.자세한 내용은 참고 사항을 참조하십시오.[37]
역사
실험실에서 Z-핀치를 처음 만든 것은 1790년 마르티누스 판 마름이 100개의 레이든 항아리를 철사로 방류하여 폭발을 일으켰을 때일 것이다.[39]이 현상은 폴락과 배러클로가[1] 번개에 맞은 후 피뢰침에서 동관이 압축되고 왜곡된 길이를 조사했던 1905년이 되어서야 이해되었다.그들의 분석은 큰 전류 흐름과 자기장의 상호작용에 의한 힘이 압축과 왜곡을 야기했을 수 있다는 것을 보여주었다.[40]액체 금속의 핀치 효과에 대한 유사하고 명백하게 독립적인 이론적 분석은 1907년 Northrupp에 의해 발표되었다.[41]그 다음 주요 발전은 베넷이[42] 정적 Z-핀치의 방사형 압력 균형에 대한 분석을 1934년에 발표한 것이다(자세한 내용은 다음 절 참조).
그 후 핀치에 대한 실험적이고 이론적인 진보는 핵융합 발전 연구에 의해 추진되었다.M G 헤인즈 외 연구진은 "Wire-array Z-pinch: ICF용 강력한 X선 소스"에 대한 기사에서 "Z 핀치의 초기 역사"[43]에 대해 썼다.
- 1946년 톰슨과 블랙먼은 추가적인 수직 자기장을 가진 토로이드 Z-핀치를[44] 기반으로 한 핵융합로 특허를 출원했다.그러나 1954년 Kruskal과 Schwarzschild는[45] 그들의 MHD 불안정 이론을 Z-pinch에 발표했다.1956년 쿠르차토프는 중수소 핀치에서 비열 중성자와 m = 0, m = 1 불안정성을 보여주는 유명한 하웰 강의를 했다.[46]1957년 Pease와[47] Braginskii는[48][49] 수소에서 전류가 1.4 MA를 초과할 때 압력 밸런스 하에 Z-pinch에서 복사 붕괴를 독립적으로 예측했다. (위에서와 내부에서[50] 논의된 자기 에너지의 저항성 소산보다는 점성이지만 복사 붕괴를 방지한다.)
1958년 로스앨러모스 국립연구소에서 실라 1세라는 이름의 세타핀치 기계를 사용하여 세계 최초로 제어된 열핵융합실험이 이루어졌다.중수소가 가득 찬 실린더는 플라즈마로 변환되어 세타핀치 효과로 섭씨 1,500만도로 압축되었다.[7]마지막으로, 1960년 R 라담 주도의 임페리얼 칼리지에서는 고원-레이틀리의 불안정성이 나타났고, 성장률은 동적 Z-핀치로 측정되었다.[51]
평형분석
원차원
플라즈마 물리학에서는 일반적으로 θ-핀치, Z-핀치, 나사 핀치 등 세 가지 핀치 형상이 연구된다.이것들은 원통형이다.실린더는 축 방향(z)과 방위 방향(dimmuthal) 방향에서 대칭이다.1차원 핀치는 전류가 이동하는 방향을 가리키는 이름이다.
θ-pinch
θ-pinch는 z 방향으로 향하는 자기장과 θ 방향으로 향하는 큰 직경 전류를 가지고 있다.Ampere의 법칙 사용(변위 용어 무시)
B는 r의 함수일 뿐이므로 우리는 이것을 다음과 같이 단순화할 수 있다.
그래서 J는 θ 방향을 가리킨다.
따라서 에 평형 조건( = j×B {\p=\ \ \)은 다음과 같다.
θ핀은 혈장 불안정성에 내성이 있는 경향이 있다.이것은 부분적으로 알펜의 정리(동결유속 정리라고도 한다) 때문이다.
Z-핀치
Z-핀치는 θ 방향의 자기장과 z 방향으로 흐르는 전류 J를 가지고 있다.다시 말하지만, 정전 암페어의 법칙에 따르면
따라서 에 대한 평형 조건인 p= .
플라즈마 안의 입자들은 기본적으로 자기장 선을 따르기 때문에, Z 핀치는 그들을 원을 그리며 이끈다.따라서, 그들은 뛰어난 구속 특성을 갖는 경향이 있다.
나사가 끼다.
나사 핀치는 θ핀치의 안정성 측면과 Z핀치의 구속 측면을 결합하기 위한 노력이다.암페어의 법칙을 다시 한 번 언급하면서
그러나 이번에 B분야는 θ 성분과 z 성분으로 되어 있다.
그래서 이번에 J는 z방향에 구성요소가 있고 direction방향에 구성요소가 있다.
마지막으로 스크루 핀치의 평형 조건 = p)은 다음과 같다.
충돌 광학 장치를 통한 나사 끼임
나사 핀치는 초경량 지속시간의 광학적 병균을 충돌하여 레이저 플라즈마에서 생성될 수 있다.[52]이러한 목적을 위해 광학 용품은 위상 결합되어야 한다.[53]자기장 분포는 Ampere의 법칙을 통해 여기서 다시 주어진다.
2차원
1차원 핀치의 공통적인 문제는 최종 손실이다.입자의 움직임의 대부분은 자기장을 따라 움직인다.θ-pinch와 스크루-pinch로, 이것은 기계의 끝부분에서 입자를 매우 빠르게 유도하여 질량과 에너지의 손실을 초래한다.이 문제와 함께 Z-핀치에는 주요 안정성 문제가 있다.입자는 자석 거울로 어느 정도 반사될 수 있지만 이마저도 많은 입자가 통과할 수 있게 한다.이러한 최종 손실을 이기는 일반적인 방법은 실린더를 토러스 모양으로 구부리는 것이다.불행하게도 이것은 토러스 내부 부분(상측)의 경로가 외측(외측)의 유사한 경로보다 짧기 때문에 θ 대칭을 깨트린다.따라서 새로운 이론이 필요하다.이것은 유명한 그라드-샤프라노프 방정식을 만들어낸다.Grad-Shafranov 방정식에 대한 수치적 해결책도 일부 평형을 산출했으며, 특히 필드 핀치 역전의 평형을 산출했다.
삼차원
2015년[update] 현재 3차원 평형성에 대한 일관된 분석 이론이 없다.그러한 평형을 찾는 일반적인 접근법은 진공 이상 MHD 방정식을 해결하는 것이다.수치 해법은 항성기에 대한 설계를 산출했다.일부 기계는 헬리컬 대칭과 같은 단순화 기법을 이용한다(예: 위스콘신 대학의 헬리컬 대칭 eXperiment).그러나 임의의 3차원 구성의 경우 1-D 구성과 유사한 평형 관계가 존재한다.[54]
여기서 κ은 곡률 벡터로서 다음과 같이 정의된다.
b 단위 벡터가 B에 접하는 경우.
형식적 처리
베넷의 관계
축전류 밀도, j 및 관련 방위 자기장 B를 생성하는 축전장이 있는 완전 이온화된 퀘이네우트랄 플라즈마의 원통형 기둥을 고려한다.전류가 자기장을 통해 흐를 때, 핀치는 내부 방사상 힘 밀도 j x B로 생성된다.힘의 균형을 유지하는 안정된 상태에서:
여기서 ∇p는 자압 구배, p와e p는i 각각 전자와 이온 압력이다.그런 다음 맥스웰의 B = j 을(를) 사용하고 이상적인 가스 p= k 을(를)로 도출한다
- }}}}베넷 관계)
여기서 N은 축을 따라 단위 길이당 전자 수, T와e T는i 전자와 이온 온도, 나는 총 빔 전류, k는 볼츠만 상수다.
일반화된 베넷 관계
일반화된 Bennett 관계는 각도 주파수 Ω에서 회전을 진행하는 전류를 운반하는 자기장 정렬 원통형 플라즈마 핀치를 고려한다.플라즈마 실린더의 축을 따라 전류 밀도 j를z 흐르면서 방위각 자석 β가φ 발생한다.원래 위탈리스에 의해 파생된 일반화된 베넷 관계는 다음과 같은 결과를 낳는다.[57][58]
- 전류가 흐르는 자기장 정렬 원통형 플라즈마가 반경 a를 갖는 경우,
- J는0 z축에 대한 관성의 총 모멘트,
- W는⊥kin 빔 축을 가로지르는 빔 모션으로 인한 단위 길이당 운동에너지다.
- W는Bz 단위 길이당 자체 정합성이 보장되는z B 에너지다.
- W는Ez 단위 길이당 자체 정합성이 보장되는 Ez 에너지 입니다.
- W는k 단위 길이당 열역동학 에너지임
- I(a)는 반지름 a 내부의 축 전류(r in diagram)이다.
- N(a)는 단위 길이당 총 입자 수입니다.
- E는r 방사형 전기장이다.
- E는φ 회전 전기장이다.
방정식의 양항은 팽창력이고 음항은 빔 압축력을 나타낸다.
칼크비스트의 관계
1988년 퍼 칼크비스트가 발표한 칼크비스트 관계는 운동 압력이 내부보다 핀치 경계에 훨씬 작은 경우를 위해 일반화된 베넷트 관계(위)의 전문화다.[12]그것은 형식을 취한다.
그리고 많은 공간 플라스마에도 적용된다.
칼크비스트 관계는 베넷 핀치에서 총 전류(I) 대 단위 길이당 입자 수(N)를 보여 주는 그림(오른쪽 참조)으로 나타낼 수 있다.이 차트는 물리적으로 구별되는 네 개의 영역을 보여준다.플라즈마 온도는 상당히i 차갑다(T = T = T = Ten = T = 20 K), 주로 평균 입자 질량이 3×10−27 kg인 수소를 포함한다.열역학 에너지k W >> πa2 pk(a).곡선, ΔW는Bz 축 자기장z B로 인해 단위 길이당 초과 자기 에너지의 양을 다르게 보여준다.플라즈마는 비회전성으로 가정되며, 가장자리의 운동 압력은 내부보다 훨씬 작다.
차트 지역:왼쪽 위 지역에서는(를), 작동 힘이 우성. 바닥을 향하여(b), 바깥쪽으로 운동 압력 균형 안에서 자기 기압, 전체 압력은 한결같다.(c)은 자기 압력은 중력 균형 맞추어 조정이 수직선 ΔWBz=0, 작동 힘의 오른쪽 무시할 수 있다.(d)은.l경사 곡선 ΔWBz = 0의 eft, 중력은 무시할 수 있다.차트는 칼크비스트 관계의 특별한 경우를 보여주며, 보다 일반적인 베넷 관계로 대체되는 경우 차트의 지정된 영역은 유효하지 않다는 점에 유의한다.
Carlqvist는 위의 관계와 파생상품을 사용함으로써 베넷 핀치, 청바지 기준(중력 불안정성의 경우 1차원과 2차원의 경우),[59] 무력 자기장, 중력 균형 자압 및 이들 상태 사이의 연속적인 전환을 설명할 수 있다는 점에 주목한다.
문화권 참조사항
오션스 일레븐에서는 가상화된 대칭 발생 장치가 사용되었는데, 이 장치는 등장인물들이 히스트를 시작할 수 있을 정도로 충분히 오랫동안 라스베가스의 전력망을 방해하기 위해 사용되었다.[60]
참고 항목
참조
- ^ a b 폴록 J A와 배러클러프 S(1905) Proc. R. Soc. 뉴사우스웨일스 39131
- ^ Buneman, O. (1961). "The Bennett Pinch". In Drummond, James E. (ed.). Plasma Physics. New York: McGraw-Hill. p. 202. Bibcode:1961plph.conf..202B. LOC 60-12766.
- ^ Lee, S. (1983). "Energy balance and the radius of electromagnetically pinched plasma columns". Plasma Physics. 25 (5): 571–576. Bibcode:1983PlPh...25..571L. doi:10.1088/0032-1028/25/5/009.
- ^ Schmidt, Helmut (1966). "Formation of a Magnetic Pinch in InSb and the Possibility of Population Inversion in the Pinch". Physical Review. 149 (2): 564–573. Bibcode:1966PhRv..149..564S. doi:10.1103/physrev.149.564.
- ^ Severnyi, A. B. (1959). "On the Appearance of Cosmics Rays in the Pinch Effect in Solar Flares". Soviet Astronomy. 3: 887. Bibcode:1959SvA.....3..887S.
- ^ Zueva, N. M.; Solov'ev, L. S.; Morozov, A. I. (1976). "Nonlinear instability of plasma pinches". Journal of Experimental and Theoretical Physics Letters. 23: 256. Bibcode:1976JETPL..23..256Z.
- ^ a b Phillips, James (Winter 1983). "Magnetic Fusion". Los Alamos Science. pp. 64–67.
- ^ Rai, J.; Singh, A. K.; Saha, S. K (1973). "Magnetic field within the return stroke channel of lightning". Indian Journal of Radio and Space Physics. 2: 240–242. Bibcode:1973IJRSP...2..240R.
- ^ Galperin, Iu. I.; Zelenyi, L. M.; Kuznetsova, M. M. (1986). "Pinching of field-aligned currents as a possible mechanism for the formation of raylike auroral forms". Kosmicheskie Issledovaniia. 24: 865–874. Bibcode:1986KosIs..24..865G.
- ^ Syrovatskii, S. I. (1981). "Pinch sheets and reconnection in astrophysics". Annual Review of Astronomy and Astrophysics. 19: 163–229. Bibcode:1981ARA&A..19..163S. doi:10.1146/annurev.aa.19.090181.001115.
- ^ Airapetyan, V. S.; Vikhrev, V. V.; Ivanov, V. V.; Rozanova, G. A. (1990). "Pinch Mechanism of Energy Release of Stellar Flares". Astrophysics. 32 (3): 230–235. Bibcode:1990Ap.....32..230A. doi:10.1007/bf01005504. S2CID 120883355.
- ^ a b Carlqvist, Per (May 1988). "Cosmic electric currents and the generalized Bennett relation". Astrophysics and Space Science. 144 (1–2): 73–84. Bibcode:1988Ap&SS.144...73C. doi:10.1007/BF00793173. S2CID 119719745.
- ^ Biskamp, Dieter (1997). Nonlinear Magnetohydrodynamics. Cambridge, England: Cambridge University Press. p. 130. ISBN 0-521-59918-0.
- ^ Basu, Dipak K. (8 October 2018). Dictionary of Material Science and High Energy Physics. p. 315. ISBN 978-0-8493-2889-3.
- ^ Srivastava, K. M.; Vyas, D. N. (August 1982). "Non-linear analysis of the stability of the screw pinch". Astrophysics and Space Science. 86 (1): 71–89. Bibcode:1982Ap&SS..86...71S. doi:10.1007/BF00651831. S2CID 121575638.
- ^ I.H.에 의한 플라즈마 물리학에 대한 소개에서 "MHD Equilibria"를 참조하십시오.허친슨(2001)
- ^ Srivastava, K. M.; Waelbroeck, F. (1976). "On the stability of the screw pinch in the CGL model". Journal of Plasma Physics. 16 (3): 261. Bibcode:1976JPlPh..16..261S. doi:10.1017/s0022377800020201.
- ^ Anderson, O. A.; Furth, H. P.; Stone, J. M.; Wright, R. E. (November 1958). "Inverse Pinch Effect". Physics of Fluids. 1 (6): 489–494. doi:10.1063/1.1724372.
- ^ Helander, P.; Akers, R. J.; Valovič, M. (3 November 2005). "The effect of non-inductive current drive on tokamak transport". Plasma Physics and Controlled Fusion. 47 (12B): B151–B163. Bibcode:2005PPCF...47B.151H. doi:10.1088/0741-3335/47/12b/s12.
- ^ 플라즈마 물리학:제3판" 266페이지 https://books.google.co.uk/books?id=4cHkd77TSHcC&pg=PA266&dq=Ware+pinch&hl=en&sa=X&ei=aZsVVdvZF5L8gwSO_oDoDw&ved=0CCYQ6AEwAQ#v=onepage&q=Ware%20pinch&f=false
- ^ Slutz, Stephen; Vesey, Roger A. (2012). "High-Gain Magnetized Inertial Fusion". Physical Review Letters. 108 (2): 025003. Bibcode:2012PhRvL.108b5003S. doi:10.1103/PhysRevLett.108.025003. PMID 22324693.
- ^ Hardee, P. E. (1982). "Helical and pinching instability of supersonic expanding jets in extragalactic radio sources". Astrophysical Journal. 257: 509–526. Bibcode:1982ApJ...257..509H. doi:10.1086/160008.
- ^ Pereira, N. R.; et al. (1988). "X-rays from Z-pinches on relativistic electron-beam generators". Journal of Applied Physics. 64 (3): R1–R27. Bibcode:1988JAP....64....1P. doi:10.1063/1.341808.
- ^ Wu, Mei; Chen, Li; Li, Ti-Pei (2005). "Polarization in Gamma-Ray Bursts Produced by Pinch Discharge". Chinese Journal of Astronomy & Astrophysics. 5 (1): 57–64. arXiv:astro-ph/0501334. Bibcode:2005ChJAA...5...57W. doi:10.1088/1009-9271/5/1/007. S2CID 121943.
- ^ A.L. Peratt, "접힌 입자 빔으로부터의 싱크로트론 방사능", (1998) 플라즈마 물리학: VII Ropp 97: 1997년 중남미 플라즈마 물리학 워크숍의 진행, 파블로 마틴, 훌리오 푸에르타, 파블로 마르멘 편집, 메이로비치, B. E. "자성 붕괴"를 참조. 안정성, 방사선 방출 및 밀집 핀치의 진화의 문제"(1984) 물리학 보고서, 104권, 5권, 259-346.
- ^ Anderson, Oscar A.; et al. (1958). "Neutron Production in Linear Deuterium Pinches". Physical Review. 110 (6): 1375–1387. Bibcode:1958PhRv..110.1375A. doi:10.1103/physrev.110.1375.
- ^ Ryutov, D. D.; Derzon, M. S.; Matzen, M. K (2000). "The physics of fast Z pinches". Reviews of Modern Physics. 72 (1): 167–223. Bibcode:2000RvMP...72..167R. doi:10.1103/revmodphys.72.167.
- ^ Andre Gsponer, "외기 및 외부 공간 플라스마에서의 고강도 고에너지 입자 빔 전파 물리학"(2004) https://arxiv.org/abs/physics/0409157
- ^ Peratt, Anthony L, "플라즈마 우주에서 입자 빔과 전류의 역할"(1988) 레이저 및 입자 빔 (ISSN 0263-0346) 1988년 8월 6일 페이지 471-491.
- ^ "Z-핀치 펄스 플라즈마 추진 기술 개발" 최종 보고서 고급 개념 사무소(ED04) 마셜 우주 비행 센터 2010년 10월 8일, 타라 폴스그로브, 에트알.
- ^ http://dorland.pp.ph.ic.ac.uk/magpie/?page_id=239 Wayback Machine "Wire Arrays Z-Pinche"에 액세스한 2014-11-05 아카이브: 3-27-2015
- ^ LaPointe, Robert. "High Voltage Devices and Experiments". Retrieved February 21, 2013.
- ^ Tristan. "Electromagnetic Can Crusher". Retrieved February 21, 2013.
- ^ Borros, Sam. "Solid State Can Crusher". Retrieved February 21, 2013.
- ^ "MagnetoPulS". Magnet-Physik, Dr. Steingroever GmbH. 2002. Archived from the original on 2003-05-22. Retrieved February 21, 2013.
- ^ "Industrial Application of the Electromagnetic Pulse Technology" (PDF). white paper. PSTproducts GmbH. June 2009. Archived from the original (PDF) on July 15, 2011. Retrieved February 21, 2013.
- ^ 전자파 핀치 캔 크러셔의 예는 (a) 밥 라포인트의 고전압 장치 및 실험 (b) 트리스탄의 전자파 캔 크러셔 (개략도 포함) (c) 샘 보로스의 고체 상태 캔 크러셔 (c)에서 확인할 수 있다.
- ^ IEEE 히스토리 센터, "IEEE 로고 진화" 1963년 3월 참조, "실험용 천체물리학"의 주석도 참조하십시오.
- ^ 반 마름 M 1790 Proc. 4월 4일 토요일 조밀 Z 핀치(Vancouver 1997)에 대한 콘프(Am)인스트. 물리.우드베리, 뉴욕, 1997) 프런트피스 및 pii
- ^ R. S. Pease, "전자파 핀치: 폴록에서 유럽 공동의 토러스까지", 1984년 11월 28일 시드니 대학교에서 전달된 "폴록 기념 강의" 2006-05-29 웨이백 기계에 보관
- ^ Northrup, Edwin F. (1907). "Some Newly Observed Manifestations of Forces in the Interior of an Electric Conductor". Physical Review. Series I. American Physical Society (APS). 24 (6): 474–497. Bibcode:1907PhRvI..24..474N. doi:10.1103/physrevseriesi.24.474. ISSN 1536-6065.
- ^ Bennett, Willard H. (1934). "Magnetically Self-Focussing Streams". Phys. Rev. 45 (12): 890–897. Bibcode:1934PhRv...45..890B. doi:10.1103/physrev.45.890.
- ^ Haines, M G; Sanford, T W L; Smirnov, V P (2005). "Wire-array Z-pinch: a powerful x-ray source for ICF". Plasma Phys. Control. Fusion. 47 (12B): B1–B11. Bibcode:2005PPCF...47B...1H. doi:10.1088/0741-3335/47/12b/s01.
- ^ Thompson, G. P.; Blackman; Haines, M. G. (1996). "Historical Perspective: Fifty years of controlled fusion research". Plasma Physics and Controlled Fusion. 38 (5): 643–656. Bibcode:1996PPCF...38..643H. doi:10.1088/0741-3335/38/5/001.
- ^ Kruskal, M D; Schwarzschild (1954). "Some Instabilities of a Completely Ionized Plasma". Proc. R. Soc. Lond. A. 223 (1154): 348–360. Bibcode:1954RSPSA.223..348K. doi:10.1098/rspa.1954.0120. S2CID 121125652.
- ^ 쿠르차토프 1세(1957년) J. 누클라. 에너지 4 193
- ^ Pease, R S (1957). "Equilibrium Characteristics of a Pinched Gas Discharge Cooled by Bremsstrahlung Radiation". Proc. Phys. Soc. Lond. 70 (1): 11–23. Bibcode:1957PPSB...70...11P. doi:10.1088/0370-1301/70/1/304.
- ^ Braginskii S I 1957 Zh. Eksp. Teor. 피즈 33 645
- ^ Braginskii S 1958 Sov. 물리적—JETP 6 494
- ^ Haines M G 등 2005년 체육. 레트 목사님..제출됨. EPS Conf를 참조하십시오.Plasma Physics 2004(영국 런던) 논문 73에 수록되어 있다.
- ^ Curzon, F. L.; et al. (1960). "Experiments on the Growth Rate of Surface Instabilities in a Linear Pinched Discharge". Proc. R. Soc. Lond. A. 257 (1290): 386–401. Bibcode:1960RSPSA.257..386C. doi:10.1098/rspa.1960.0158. S2CID 96283997.
- ^ A.Yu.Okulov. "레이저 단수 테타핀치", Phys.Let.A, v.374, 4523-4527, (2010)
- ^ 광상결합과 전자기 모멘트
- ^ 이상적인 자기유체역학:에너지의 현대적 관점.제프리 P.프리드버그.매사추세츠 공과대학교.메사추세츠주 캠브리지.플레넘 프레스 - 뉴욕 및 런던 - 1987. (86, 95 페이지)
- ^ Trubnikov, Boris A (1992). "A new hypothesis of cosmic ray generation in plasma pinches". IEEE Transactions on Plasma Science. 20 (6): 898–904. Bibcode:1992ITPS...20..898T. doi:10.1109/27.199547.
- ^ 1988년 7월 국제 볼 번개 심포지엄에서 발표한 "PLASMAK 구성 및 볼 번개"(PDF Archived 2006-07-15 Wayback Machine)
- ^ Witalis, E. A. "충전된 입자 보의 플라즈마-물리적 측면"(1981) 물리적 검토 A - 일반 물리학, 3차 시리즈, 1981년 11월 24일, 페이지 2758–2764
- ^ Anthony L. Peratt, "Plasma University의 물리학", 1992년 Springer-Verlag, ISBN 0-387-9775-6
- ^ Jeans, J. H. (1902). "The stability of a spherical nebula". Phil. Trans. R. Soc. Lond. A. 199 (312–320): 1–53. Bibcode:1902RSPTA.199....1J. doi:10.1098/rsta.1902.0012.
- ^ "The Con-Artist Physics of 'Ocean's Eleven'". American Physical Society. March 2002.
외부 링크
- 전자석이 동전과 찌그러진 깡통의 예시.
- 전자화폐 수축 이론
- "분기 감소"의 알려진 역사
- 전자기력을 이용하여 정보를 파쇄할 수 있다.
- 임페리얼 칼리지 런던의 MACF 프로젝트는 전선 배열 Z-핀치 붕괴를 연구하는 데 사용된다.























 (를) 사용하고
(를) 사용하고 


![{\displaystyle {\begin{aligned}{\frac {1}{4}}{\frac {\partial ^{2}J_{0}}{\partial t^{2}}}={}&W_{\perp {\text{kin}}}+\Delta W_{E_{z}}+\Delta W_{B_{z}}+\Delta W_{k}-{\frac {\mu _{0}}{8\pi }}I^{2}(a)\\[8pt]&{}-{\frac {1}{2}}G{\overline {m}}^{2}N^{2}(a)+{\frac {1}{2}}\pi a^{2}\epsilon _{0}\left(E_{r}^{2}(a)-E_{\phi }^{2}(a)\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71e972f92a0d232a7244df3fa2ed04d57711196f)




