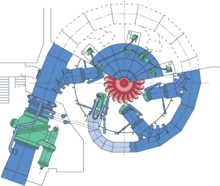
펠튼 휠

펠튼 휠 또는 펠튼 터빈은 1870년대에 ^[1]^[2]미국의 발명가 레스터 앨런 펠튼에 의해 발명된 임펄스형 수차이다.펠튼 휠은 전통적인 오버샷 워터 휠과 같은 물의 죽은 무게와는 달리, 물이 움직이는 충격에서 에너지를 추출합니다.임펄스 터빈의 많은 초기 변형이 존재했지만, 펠튼의 설계보다는 덜 효율적이었다.이러한 바퀴에서 나오는 물은 일반적으로 여전히 고속이었고, 바퀴에 전달되는 많은 동적 에너지를 빼앗아 갔다.펠튼의 패들 기하학은 가장자리가 워터제트의 절반 속도로 달릴 때 물이 매우 적은 속도로 바퀴를 떠나도록 설계되었다. 따라서 펠튼의 디자인은 물의 충격 에너지를 거의 모두 추출하여 매우 효율적인 터빈을 만들었다.

역사

Lester Allan Pelton의 1880년 10월 특허 원본에서 나온 수치입니다.

레스터 앨런 펠튼은 1829년 오하이오주 버밀리언에서 태어났다.1850년, 그는 캘리포니아 골드 러시에 참가하기 위해 육로를 여행했다.펠튼은 새크라멘토 ^[3]강에서 잡은 물고기를 파는 일을 했다.1860년, 그는 사광 채굴 활동의 중심지인 캠튼빌로 이사했다.이 시기에 많은 채굴 작업은 방대한 양의 목재를 연료로 소비하는 증기 엔진에 의해 추진되었다.몇몇 물레방아들은 더 큰 강에서 사용되었지만, 광산 근처에서 발견된 더 작은 하천에서는 효과가 없었다.Pelton은 이러한 ^[4]하천에서 발견되는 비교적 작은 흐름으로 작동하는 물레방아 설계를 수행했습니다.

1870년대 중반, 펠튼은 그의 새로운 바퀴의 나무 프로토타입을 개발했다.1876년, 그는 캘리포니아 네바다 시에 있는 광부 주조 공장에 접근하여 최초의 상업용 철 모델을 제작했습니다.최초의 펠튼 휠은 1878년 ^[4]네바다 시의 메이플라워 광산에 설치되었다.펠튼의 발명의 효율적 이점은 빠르게 인식되었고 그의 제품은 곧 높은 수요를 얻었다.그는 1880년 ^[5]10월 26일에 발명품에 특허를 취득했다.1880년대 중반까지 광부 주조 공장은 수요를 충족시킬 수 없었고, 1888년 펠튼은 자신의 이름에 대한 권리와 발명 특허를 샌프란시스코의 펠튼 워터휠 회사에 팔았습니다.그 회사는 샌프란시스코 ^[6]메인 스트리트 121/123에 공장을 설립했다.

Pelton Water Wheel Company는 전 세계에 출하된 많은 수의 Pelton Wheels를 샌프란시스코에서 생산했습니다.1892년 회사는 뉴욕시 리버티 스트리트 143번지에 동부 해안에 지점을 추가했다.1900년까지 11,000개 이상의 터빈이 사용되었습니다.1914년 회사는 샌프란시스코의 앨라배마 거리 612번지에 있는 더 큰 신규 시설로 제조를 이전했습니다.1956년 회사는 볼드윈-리마-해밀턴 회사에 인수되어 펠튼 ^[6]휠의 생산을 종료했습니다.

뉴질랜드에서는 뉴질랜드 테임즈의 A&G 프라이스가 현지 시장용 펠튼 물레방아를 생산했다.그 중 하나는 템즈 골드마인 익스피리언스에 야외 전시되어 있다.

설계.

노즐은 구동 휠(러너라고도 함)의 바깥쪽 테두리 주변에 장착된 스푼 모양의 양동이에도 강력한 고속의 물줄기를 보냅니다.워터제트가 날개에 부딪히면 수속의 방향이 날개의 윤곽을 따르도록 변화한다.워터 제트의 임펄스 에너지는 바퀴를 회전시키면서 버킷 앤 휠 시스템에 토크를 가합니다. 워터 제트는 "u-턴"을 하고 버킷의 바깥쪽으로 나가 저속으로 감속합니다.이 과정에서 워터제트의 운동량은 바퀴로 전달되고, 따라서 터빈으로 전달된다.따라서, "충격" 에너지는 터빈에 작용합니다.워터제트 속도가 회전 버킷 속도의 2배일 때 최대 출력과 효율이 달성됩니다.워터제트의 원래 운동 에너지 중 매우 적은 비율이 물 속에 남아 있으며, 이로 인해 버킷이 채워진 것과 같은 속도로 비워지고, 따라서 고압 입력 흐름이 중단되지 않고 에너지 낭비 없이 지속될 수 있습니다.

일반적으로 두 개의 버킷이 휠에 나란히 장착되고 워터 제트가 두 개의 동일한 스트림으로 분할됩니다. 그러면 휠에 가해지는 측면 부하 힘이 균형을 이루며 워터 제트에서 터빈 휠로 부드럽고 효율적으로 운동량을 전달할 수 있습니다.

물은 거의 압축할 수 없기 때문에, 거의 모든 가용 에너지가 수력 터빈의 1단계에서 추출됩니다."따라서 Pelton 휠은 압축성 유체로 작동하는 가스 터빈과 달리 터빈 단계가 하나뿐입니다."^[7]

적용들

독일 발첸제 수력 발전소의 펠튼 휠 조립체.

작은 터빈의 버킷 디테일.

펠튼 휠은 가용 수원이 낮은 유량으로 비교적 높은 유압 헤드를 갖는 수력 발전용으로 선호되는 터빈이다.펠튼 휠은 모든 크기로 제작됩니다.수력 발전소의 수직 오일 패드 베어링에 장착된 멀티톤 펠튼 휠이 있습니다.스위스 그란데 딕슨스 댐 단지에 있는 비우드론 수력 발전소의 가장 큰 유닛은 400 메가와트 ^[8]이상입니다.

가장 작은 Pelton 바퀴는 직경이 불과 몇 인치 밖에 되지 않으며 분당 몇 갤런의 흐름을 가진 산줄기로부터 동력을 얻는 데 사용할 수 있습니다.이러한 시스템 중 일부는 물을 공급하기 위해 가정용 배관 설비를 사용합니다.이러한 소형 장치는 상당한 출력 레벨을 생성하기 위해 30미터(100피트) 이상의 헤드와 함께 사용할 것을 권장합니다.물의 흐름과 설계에 따라, 이론적인 제한은 없지만 펠튼 휠은 15–1,800m(50–5,910ft)의 헤드에서 가장 잘 작동합니다.

설계 규칙

펠튼 터빈 설비의 단면도.

특정 속도 $\eta _{s}$ s \ $displaystyle \eta$ _ ${s}$ 파라미터는 $\eta _{s}$ 특정 터빈의 크기와 무관합니다.

다른 터빈 설계에 비해 펠튼 휠의 비속도는 상대적으로 낮기 때문에 기하학이 본질적으로 "저단" 설계임을 의미합니다.따라서 유량 대 압력의 비율이 낮은 수력원에 의해 공급되는 것이 가장 적합합니다(상대적으로 유량이 적거나 상대적으로 압력이 높은 것을 의미합니다).

특정 수력발전 현장을 최적의 터빈 유형과 일치시키기 위한 주요 기준은 특정 속도이다.또한 기존 기존 성능 설계에서 새로운 터빈 설계를 확장할 수 있습니다.

$\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ § $\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ = $\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ $\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ / $\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ ( $\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ ) $\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ / 4 { $displaystyle$ \ $eta _$ { $s$ } = n $rt rt$ { P } } / { \ $sqrt$ { rho } （ $gH ）^5/$ 4} $\eta _{s}=n{\sqrt {P}}/{\sqrt {\rho }}(gH)^{5/4}$ (파라미터 없음),

여기서:

$n$ {\ $displaystyle$ n $}$ = $n$ 회전 주파수(rpm)
$P$ ${displaystyle$ P $}$ = $P$ 전력(W)
$H$ {\ $displaystyle$ H $}$ = $H$ 워터헤드(m)
${\$ { $displaystyle$ \rho $\rho$ } $\rho$ = $\rho$ (kg³/m)

이 공식은 펠튼 터빈이 비교적 높은 유압 헤드 H를 가진 애플리케이션에 가장 적합하게 조정된다는 것을 암시한다. 왜냐하면 5/4 지수가 단일성보다 크고 ^[10]펠튼의 특징적인 낮은 비속도를 고려하기 때문입니다.

터빈 물리 및 파생

에너지 및 초기 분사 속도

이상적(무적)의 경우, 모든 유압 퍼텐셜 에너지(E_p = mgh)는 운동 에너지(E_k = mv²/2)로 변환된다(베르누이의 원리 참조).이 두 방정식을 동일하고 초기 제트_i 속도(V)에 대한 해는 이론적(최대) 제트 속도가 V = µ2g임을 나타냅니다_i.단순화를 위해 모든 속도 벡터가 서로 평행하다고 가정합니다.휠 러너의 속도를 (u)로 정의하면 제트가 러너에 접근할 때 러너에 대한 초기 제트 속도는 (V_i - ^[10]u)입니다.제트기의 초기 속도는 V이다_i.

최종 제트 속도

제트 속도가 러너 속도보다 높다고 가정할 때, 러너에 물이 막히지 않으면 질량 보존으로 인해 러너에 들어가는 질량은 러너에서 나가는 질량과 같아야 한다.유체는 압축할 수 없는 것으로 가정됩니다(대부분의 액체에 대해 정확한 가정).또한 제트 단면적이 일정하다고 가정한다.제트 속도는 러너에 비해 일정하게 유지됩니다.따라서 제트가 러너에서 멀어질 때 러너에 대한 제트 속도는 -(V_i - u) = -V_i + u입니다. 표준 기준 프레임(지구에 대한 기준)에서 최종 속도는 V_f =(-V_i + u) + = -V_i + 2u입니다.

최적의 휠 속도

이상적인 러너 속도는 제트 내 모든 운동 에너지가 휠로 전달되도록 합니다.이 경우 최종 제트 속도는 0이어야 한다.-V_i + 2u = 0이면 최적 러너 속도는 u = V_i /2 또는 초기 제트 속도의 절반입니다.

토크

뉴턴의 제2법칙과 제3법칙에 따르면 제트에 의해 주자에 가해지는 힘 F는 같지만 유체의 운동량 변화율과 반대이다.

F = -m(V_f_i - V)/t = -sq[(-V_i + 2u) - V_i] = -sq(-2V_i + 2u) = 2µQ(V_i - u),

여기서 θ는 밀도이고 Q는 유체 흐름의 부피 속도입니다.D가 휠 직경인 경우 러너의 토크는

T = F(D/2) = δQD(V_i - u).

러너가 정지할 때(즉, u = 0, T = δQDV_i) 토크는 최대입니다.러너의 속도가 초기 제트 속도와 같으면 토크는 0이 됩니다(즉, u_i = V이면 T = 0).토크 대 러너 속도의 그래프에서 토크 곡선은 (0, pQDV_i)와 (V_i, 0)^[10] 두 지점 사이에 직선입니다. 노즐 효율은 노즐 베이스의 수력에 대한 제트 전력의 비율입니다.

힘

검정력 P = Fu = Tθ이며, 여기서 θ는 휠의 각 속도입니다.F 대신에 P = 2µQ(V_i - u)u가 있다.최대 출력에서 러너 속도를 구하려면 u에 대한 P의 도함수를 0으로 설정합니다. [dP/du = 2µQ(V_i - 2u)]최대 전력은 u_i = V /2일 때 발생합니다.P_max = qQV_i²/2. 초기 제트 출력_i V = 22gh를 대입하면 P = ghghQ로 단순화된다_max.이 양은 제트의 운동력과 정확히 같기 때문에, 이 이상적인 경우, 제트의 모든 에너지가 ^[10]축 출력으로 변환되기 때문에 효율은 100%입니다.

효율성.

휠 동력을 초기 제트 동력으로 나눈 값이 터빈 효율, θ = 4u(V_i - u)/V입니다_i².u = 0 및 u_i = V의 경우 0입니다. 방정식에서 알 수 있듯이 실제 Pelton 휠이 최대 효율에 가깝게 작동하면 유체가 휠에서 매우 적은 잔류 속도로 ^[10]흐릅니다.이론적으로 에너지 효율은 노즐과 휠의 효율에만 따라 달라지며 유압 ^[11]헤드에 따라 달라지지 않습니다."효율"이라는 용어는 유압, 기계, 체적, 휠 또는 전체 효율을 나타낼 수 있습니다.

시스템 컴포넌트

임펄스 휠로 고압수를 운반하는 도관을 펜스톡이라고 합니다.원래 펜스톡은 밸브의 이름이었지만, 모든 유체 공급 유압 장치를 포함하도록 용어가 확장되었습니다.Penstock은 현재 임펄스 터빈을 공급하든 그렇지 ^[10]않든 압력을 받는 수로와 제어 장치의 총칭으로 사용되고 있습니다.

「」를 참조해 주세요.

레퍼런스

^ "COW THAT ASSISTED SCIENCE". The South Eastern Times. No. 1661. South Australia. 24 November 1922. p. 6. Retrieved 10 March 2017 – via National Library of Australia.
^ "MINING INTELLIGENCE". Launceston Examiner. Vol. XLV, no. 210. Tasmania, Australia. 22 August 1885. p. 3. Retrieved 10 March 2017 – via National Library of Australia.
^ Lescohier, Roger P. (2011). Lester Pelton and the Pelton Water Wheel. Nevada County Historical Society. ISBN 978-0-915641-15-4.
^ ^a ^b "Lester Allan Pelton". American Society of Mechanical Engineers.
^ 미국 특허 233692 L. A. Pelton, "Water Wheel", 1880년 10월 26일 발행
^ ^a ^b "Showplace Square Historic Resource Survey Findings" (PDF). San Francisco Planning Department. 2012.
^ Wagner, Hermann-Josef; Mathur, Jyotirmay (2011). Introduction to Hydro Energy Systems. Green Energy and Technology. Berlin, Heidelberg: Springer Berlin Heidelberg. p. 86. doi:10.1007/978-3-642-20709-9. ISBN 978-3-642-20708-2.
^ "Renewable Energy in the Heart of the Alps". Grande Dixence. Retrieved 13 August 2021.
^ Sayers, A. T. (1990). Hydraulic and Compressible Flow Turbomachines. McGraw-Hill. ISBN 978-0-07-707219-3.
^ ^a ^b ^c ^d ^e ^f Calvert, J. "Technical derivation of basic impulse turbine physics".
^ 펠튼 휠 수차, 론 앰버거스 페이지

외부 링크

Dorado Vista 목장의 하이드로 예시

[1] "COW THAT ASSISTED SCIENCE". The South Eastern Times. No. 1661. South Australia. 24 November 1922. p. 6. Retrieved 10 March 2017 – via National Library of Australia.

[2] "MINING INTELLIGENCE". Launceston Examiner. Vol. XLV, no. 210. Tasmania, Australia. 22 August 1885. p. 3. Retrieved 10 March 2017 – via National Library of Australia.

[rpl-3] Lescohier, Roger P. (2011). Lester Pelton and the Pelton Water Wheel. Nevada County Historical Society. ISBN 978-0-915641-15-4.

[asme-4] "Lester Allan Pelton". American Society of Mechanical Engineers.

[5] 미국 특허 233692 L. A. Pelton, "Water Wheel", 1880년 10월 26일 발행

[sfpd-6] "Showplace Square Historic Resource Survey Findings" (PDF). San Francisco Planning Department. 2012.

[7] Wagner, Hermann-Josef; Mathur, Jyotirmay (2011). Introduction to Hydro Energy Systems. Green Energy and Technology. Berlin, Heidelberg: Springer Berlin Heidelberg. p. 86. doi:10.1007/978-3-642-20709-9. ISBN 978-3-642-20708-2.

[GD-8] "Renewable Energy in the Heart of the Alps". Grande Dixence. Retrieved 13 August 2021.

[Sayers1990-9] Sayers, A. T. (1990). Hydraulic and Compressible Flow Turbomachines. McGraw-Hill. ISBN 978-0-07-707219-3.

[jcalvert-10] ^ ^a ^b ^c ^d ^e ^f Calvert, J. "Technical derivation of basic impulse turbine physics".

[11] 펠튼 휠 수차, 론 앰버거스 페이지

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[10]

[11]

v t 수력 발전
수력 발전	댐 재래식 수력발전소 목록 양수식 수력 발전 소형 수력 마이크로 하이드로 피코 하이드로 하천 수력 발전
수력 발전 설비	프란시스 터빈 카플란 터빈 타이슨 터빈 갈로프 헬리컬 터빈 펠튼 휠 터고 터빈 직류 터빈 물레방아

Search

펠튼 휠

네임스페이스

더

목차

역사

설계.

적용들

설계 규칙

터빈 물리 및 파생

에너지 및 초기 분사 속도

최종 제트 속도

최적의 휠 속도

토크

힘

효율성.

시스템 컴포넌트

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

펠튼 휠

역사

설계.

적용들

설계 규칙

터빈 물리 및 파생

에너지 및 초기 분사 속도

최종 제트 속도

최적의 휠 속도

토크

힘

효율성.

시스템 컴포넌트

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.