반도체 레이저의 비선형 이론
Nonlinear theory of semiconductor lasers
Fabry-Perot(FP) 반도체 레이저의 레이저 이론은 이득, [1][2]굴절률[3], 손실 계수가[4] 에너지 유량의 함수인 만큼 비선형임이 입증된다.비선형 이론은[2] 다른 이론적 모델에 기초해 설명조차 할 수 없는 몇 가지 실험(예를 들어 자연 선폭)을 설명할 수 있게 했다. 이는 개발된 비선형 이론이 레이저 이론의 새로운 패러다임임을 시사한다.
게인 매체에서의 방정식
맥스웰 방정식은 수동적 매체에 대한 필드를 설명하며 레이저 및 양자 증폭기에 있는 필드를 설명하는 데 사용할 수 없다.현상학적 방정식은 게인 매체에서 전자기장에 대해, 즉 게인 매체에 대한 맥스웰의 방정식과 이러한 방정식에 대한 포앵팅의 정리에서 도출된다.[1][2][5]이득 매체에 있는 맥스웰 방정식은 에너지 유량에 대한 방정식을 얻고 비선형 위상 효과를 설명하기 위해 사용된다.[1][2][5]
우리는 η을 특정한 이득 인자로 정의했다; σ은 일관성 없는 손실(예를 들어 자유 전자에 대한)을 설명하는 특정한 전도성이다.다른 맥스웰 방정식은 변경되지 않고 사용된다.
포아닌팅 정리는 (1)-(3)에서 다음과 같이 한다.
여기서 S는 Poynting 벡터; V=sz, 0<z>, 여기서 s는 활성 레이저 매체의 단면(축 z)이다.
에너지 유량에 대한 방정식은 (4)부터 다음과 같다.
어디에
여기서 은(는) 에너지 플럭스, s 은(는) 레이저 활성 구역의 단면적, 는) 구속 계수, 은 흡수 계수 아웃이다.ide active zone; is losses due to incoherent scattering; is two-photon absorption factor;[2][4] and ).
선 모양 및 자연 선폭에 대한 공식
반도체 레이저의 자연 선폭 이론은 FP 레이저의[3][5] 굴절률 n과 DFB(Distributed FeedBack[5][6]) 레이저의 유효ef 굴절률 n이 E의 기능이라는 점에 따라 개발되었다.
FP 및 DFB 레이저의 선 모양 공식은 도출되었다.선 모양에 대한 이러한 공식은 유사하며 다음과 같은 형식을 가지고 있다.
여기서 = - L v L은(는) 레이저 생성 주파수,
여기서 D 1, {\D_{1},}}: FP와 DFB 레이저의[2][6][7][8] 형식이 서로 다르다.[9] 자연 선폭 Δν를 쓰자.
여기서 T((인류 W) p는 P+B){\displaystyle T\left(\left(mW\right){\frac{A_{아빠}}{P}}+B\right)}은 그 다리 함수[2][8][9]Δ v({\displaystyle\Delta v^{(c)}}와 P({\displaystyle P^{(c)}}은 특성 선폭 및 특성 레이저 전력;k은 특성 매개 변수이다. 레이저가 없비선형성, q는 비차원 역동력:
반도체 레이저의 자연 선폭 이론은 독자적인 의의를 갖고 있다.이와 동시에 개발된 이론은 레이저의 비선형 이론의 불가결한 부분이며, 그 개념과 도입된 특성 매개변수가 비선형 이론의 모든 부분에 사용된다.
반도체 레이저의 이득
이완과 함께 밀도 행렬 방정식을 사용하여 다음과 같은 도출이 이루어졌다.반도체 레이저에서 아인슈타인의 스펙트럼 계수와 그에 따라 아인슈타인의 계수;[1][2][10] 반도체 레이저에서 포화 효과의 공식; 반도체 레이저에서 포화 효과가 작은 것으로 나타났다.[1][2]반도체 레이저의 이득은 이완과 함께 밀도 행렬 방정식을 사용하여 도출되었다.[1][2]파브리-페로 레이저 이득은 에너지 플럭스에 따라 달라지며, 이는 반도체 레이저의 '기본 비선형 효과'를 결정하는 것으로 나타났다.
어디에
여기서 B 는 협대역 파형에 노출되었을 때 두 에너지 수준 사이의 유도 전환에 대한 아인슈타인 계수로서 다음과 같은 형태로 기록된다.[2][10]
where is effective natural linewidth; is the energy flux; is전환의 스펙트럼 밀도
1종 유도방사선 필요조건
제1종과 제2종의 유도 방사선에 필요한 조건은 다음과 같다.[1][2]유도 방사선에 필요한 조건은 이득이 0보다 큰 요건에 의해 결정된다.베르나르와 두라푸르에[2][11] 의해 공식화된 제1종류의 유도 방사선에 필요한 조건은 위에 위치한 레벨의 모집단이 아래 위치한 레벨의 모집단보다 많아지는 것이다.
2종 유도방사선 필요조건
노페가[1][2] 공식화한 제2종 유도 방사선의 필요조건은 다음과 같다.
두 번째 종류의 유도 방사선의 필요조건은 레이저 용량의 기본적 제한을 형성할 수 있으며,[1][2] 이는 다음과 같이 실험적으로 확인되었다.
여기서 은(는) 에너지 플럭스, () 은 궁극적인 힘의 특성 매개변수다.그림 1은 특성 파라미터의 두 세트에 대한 g (를 보여준다.
실험 시뮬레이션
4.1. 이득 매체에 있는 맥스웰의 방정식은 에너지 유량에 대한 방정식을 얻기 위해 사용된다.[1][2][5]비선형 위상 효과는 [1][2]굴절률의 비선형성을 이용하여 설명하고 시뮬레이션하였다([3]그림 3 참조).
뺐는다. 실험적 출력 특성을 모의 실험해 왔다 선진 이론,:자연 선폭(시뮬레이션을 보in,[2][6])(그림 2 보), 실험 와트-암페어 characteristics[1][2][11](Fig.4 보), 실험적인 출력 복사 line-length의 현재에 소인형 패브리 페로 반도체 주입 lasers,[1][2]에 의존에 따르면(F. 보Ig.3 탭뿐만 아니라 lin.ewidth in DFB 레이저(시뮬레이션 인,[7][8] 참조)생성된 이론은 Fabry-Perot 레이저 및 분산 피드백 DFB 레이저의[2][6][7][8][9][12] 자연 선폭 측정에 대해 두 가지 방법(13)과 (15)의 도움을 받아 대부분의 발표된 실험을 시뮬레이션할 수 있게 한다.선 모양에 대해 도출된 공식을 바탕으로 Fabry-Perot 레이저의 자연 선폭 측정 실험(예: 그림.2 참조) 12건과 DFB 레이저의[2][9] 실험 15건을 시뮬레이션했다.[2][6]자연 선폭에 대해 도출된 공식을 바탕으로 파브리-페로 레이저에서[2][6] 자연 선폭을 측정하는 15가지 실험과 DFB 레이저에서[2][9] 15가지 실험을 시뮬레이션했다.[2][6][8]방사선의 라인 형태에[2][6][12] 대한 파생 공식(FP 레이저 및 DFB 레이저[2][7])은 로렌츠 라인 공식과 구별된다.
4.3. 실험적 출력 특성을 모의 실험해 왔다 선진 이론,:자연 선폭(시뮬레이션을 보in,[5][7]), 실험 와트-암페어 characteristics[10](Fig.4 보), 그리고 실험 출력 복사 line-length의 소인형 패브리 페로 반도체 주입 lasers[13](Fig.3 보), 뿐만 아니라 미스터리 한에서 현재에 의존에 기초를 둔다.DF에 newidthB 레이저(시뮬레이션 인,[2][9] 참조)
4.4. 비선형 이론에 기초하여 자연 선폭이 작은 레이저와 출력 전력이 더 높은 레이저를 개발할 것을 권고하였다.[1][2]
결론
밀도 매트릭스 방정식의 해법에 기초하여 유도 전환에 대한 아인슈타인 계수가 도출되었으며, 반도체 레이저의 경우 포화 효과가 작다는 것이 밝혀졌다.[1][2]에너지 유량에 따른 이득의 공식은 레이저의 기본적인 비선형 효과다.비선형성을 초래하는 주효과는 포화효과라고 명시되어 있다.[1][2]반도체 레이저의 경우 포화 효과는 미미하다.우리는 밀도 행렬 방정식과 자연 선폭에 대한 표현을 바탕으로 Fabry-Perot 반도체 레이저의 이득 g를 도출했다.[1][2]따라서 선폭 이론은[2][8][9] 비선형 이론의 필수적인 부분이다.결과 g의 에너지 플럭스에 대한 의존성은 반도체 레이저의 주요 비선형 효과라고 불렸다.[1][2] 이 관계 공식의 도출은 다음과 같다.[1][2]실험 파장 이동 대 정규화된 전류(J/Jth), 내인성 반도체의 양자 유정을 가진 고출력 레이저에 대해 출력 전력 대 전류를 시뮬레이션했다.다른 효과로 인한 상태 밀도의 확대가 고려되었다.비선형 이론은 다른 이론적 모델에 기초해 설명조차 할 수 없는 몇 가지 실험(예를 들어 자연 선폭)을 설명할 수 있게 했다. 이는 개발된 비선형 이론이 레이저 이론의 새로운 패러다임임을 시사한다.비선형 이론 개발로 인해 자연 선폭이 작은 레이저와 출력 전력이 높은 레이저를 만들 수 있는 권고안이 제시될 수 있다.
참조
- ^ a b c d e f g h i j k l m n o p q r s t u v w 반도체 레이저의 비선형 이론에 관한 노페 M G. 2016 레이저 물리. 26055004 (doi:10.1088/1054-660X/26/5/055004)
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq 노페 M.G. "반도체 레이저용 비선형 이론의 기초"(출판사 SB RAS, 2016)노보시비르스크, 2016).(단노그래프를 구입하려면 "반도체 레이저에 대한 비선형 이론의 기초" 링크를 사용하십시오.)
- ^ a b c 파르토비와 E.M.Garmire, J. Appl.체육, 69, 6885 (1991년).
- ^ a b A 등이 말했다.opt. soc. am.B 1992년 9월 405년
- ^ a b c d e f 노페 M G 반도체 레이저의 비선형 굴절; 실험 시뮬레이션, J. Mod. 2004 51 153
- ^ a b c d e f g h i 노페 M G, Fabry-Perot Semiconductor Laser, Laser Phys, 24, 125006 (2014)DOI:10.1088/1054-660X/24/12/125006
- ^ a b c d e 노페 M G. 분산 피드백 레이저의 자연 선폭에 관한; 실험의 시뮬레이션.Proc. XII 인턴에서.(APEIE – 2014)- v.1, 페이지 456 - 460)
- ^ a b c d e f g 노페 M G. Fabry-Perot 레이저의 자연 선폭에 대한 공식; In Proc. XII 인턴 실험의 시뮬레이션.(APEIE – 2014)- v.1, 페이지 472 - 477)
- ^ a b c d e f g h 분산 피드백 레이저의 자연 선폭에 대한 Nope M G On 공식; 실험 시뮬레이션.Proc. XII 인턴에서.(APEIE – 2014)- v.1, 페이지 461 - 467
- ^ a b c 노페 M. G. 이완 기술 물리학 문자 2000, V. 26, 10-11의 시스템 자극 전환의 공진 및 비저항 계수
- ^ a b c 안드리프, A.유, 외반도체, 2009,43 543-547
- ^ a b 노페 M.G. on the Line Form and Natural Linewidth; 실험의 시뮬레이션과 해석Proc. XII 인턴에서.(NUSOD-2012), 123.
- ^ 버나드 M.G. 듀라푸르 G. 1961 체육관상태 솔리디 127 699
- ^ Elsasser W, Gobel E.O, Kuhl J, IEEE JQE,1983 19 981
- ^ 이토 M, 키무라 T 1980 IEEE J. QE 16 910







 (는) 에너지 플럭스, s
(는) 에너지 플럭스, s  (는) 레이저 활성 구역의 단면적,
(는) 레이저 활성 구역의 단면적,  ) 구속 계수
) 구속 계수







 (는) 레이저 생성 주파수,
(는) 레이저 생성 주파수,











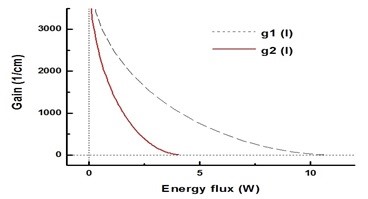



 궁극적인 힘의 특성 매개변수다.그림 1은 특성 파라미터의 두 세트에 대한
궁극적인 힘의 특성 매개변수다.그림 1은 특성 파라미터의 두 세트에 대한




