비결정론적 유한 오토마톤

(0 ^*1) 1 (0 ³1)의 NFA.
해당 언어의 DFA에는 적어도 16개의 상태가 있습니다.

오토마타 이론에서, 유한 상태 기계는 결정론적 유한 오토마톤(DFA)이라고 불린다.

각각의 전이는 소스 상태와 입력 기호에 의해 고유하게 결정된다.
각 상태 전환에는 입력 기호를 읽어야 합니다.

Non-deterministic finite automaton(NFA; 비결정적 유한 오토마톤) 또는 비결정적 유한 상태 기계는 이러한 제약사항을 따를 필요가 없습니다.특히, 모든 DFA는 NFA이기도 합니다.NFA라는 용어는 DFA가 아닌 NFA를 가리켜 좁은 의미로 사용되는 경우가 있지만 이 문서에서는 사용되지 않습니다.

서브셋 구성 알고리즘을 사용하여 각 NFA를 동등한 DFA, 즉 동일한 형식 ^[1]언어를 인식하는 DFA로 변환할 수 있습니다.DFA와 마찬가지로 NFA는 정규 언어만 인식합니다.

NFA는 1959년 마이클 O. 라빈과 다나 ^[2]스콧에 의해 도입되었으며, 그들은 또한 DFA와 동등함을 보여주었다.NFA는 정규 표현의 구현에 사용됩니다.Thompson의 구성은 문자열 패턴 매칭을 효율적으로 수행할 수 있는 NFA에 정규식을 컴파일하는 알고리즘입니다.반대로, Kleene의 알고리즘을 사용하여 NFA를 정규식으로 변환할 수 있습니다(입력 오토마톤에서는 일반적으로 크기가 기하급수적입니다).

NFA는 여러 가지 방법으로 일반화되었다. 예를 들어, θ-moves, 유한 상태 변환기, 푸시다운 오토마타, 교대 오토마타, θ-오토마타 및 확률론적 오토마타이다.DFA 외에 NFA의 다른 알려진 특별한 경우로는 모호하지 않은 유한 오토마타(UFA)와 자기 검증 유한 오토마타(SVFA)가 있다.

비공식 소개

NFA의 동작을 설명하는 방법은 두 가지가 있으며, 두 가지 모두 동일합니다.첫 번째 방법은 NFA라는 이름으로 비결정론을 이용한다.각 입력 기호에 대해 NFA는 모든 입력 기호가 소비될 때까지 새 상태로 전환됩니다.각 단계에서 자동화는 비결정적으로 적용 가능한 전환 중 하나를 "선택"입력을 완전히 소비한 후 수용 상태로 이어지는 일련의 선택과 같은 적어도 하나의 "행운의 실행"이 존재하는 경우, 수락됩니다.그렇지 않으면, 즉 선택 시퀀스가 모든 입력을^[3] 소비하여 수용 상태로 이어질 수 없는 경우 입력은 ^[4]^{: 19}^[5]^{: 319}거부됩니다.

두 번째 방법으로 NFA는 입력 심볼의 열을 하나씩 소비합니다.각 단계에서 두 개 이상의 전환이 적용될 때마다 자신을 적절한 수의 복사본으로 "클론화"하고 각 복사본은 서로 다른 전환에 따릅니다.적용할 수 있는 전환이 없는 경우 현재 복사본은 막다른 골목에 있으며 "디지"합니다.입력 전체를 소비한 후 복사본 중 하나가 승인 상태가 되면 입력이 받아들여지고 그렇지 않으면 ^[4]^{: 19–20}^[6]^{: 48}^[7]^{: 56}거부됩니다.

형식적 정의

정식 정의에 대한 보다 기본적인 소개는 오토마타 이론을 참조하십시오.

오토마톤

NFA는 5개의 태플 $, 0$ $0, F$ 로 정식으로 표현되며 다음과 같이 $구성$ 됩니다.

유한 $상태$ Q $(\displaystyle$ Q $Q$
입력 기호 $\Sigma$ (\ $displaystyle \Sigma$ 의 유한 세트.
$\delta$ 함수 ${\$ { $displaystyle$ \ $times }$ : $Q\times \Sigma \rightarrow {\mathcal {P}}(Q)$ × $Q\times \Sigma \rightarrow {\mathcal {P}}(Q)$ $Q\times \Sigma \rightarrow {\mathcal {P}}(Q)$ P ( $Q\times \Sigma \rightarrow {\mathcal {P}}(Q)$ ) \ $displaystyle$ Q \ $times$ \ $Sigma$ \ $rightarrow$ \ $mathcal$ { $P}$ （ $Q$ ） $Q\times \Sigma \rightarrow {\mathcal {P}}(Q)$ 。
초기(또는 시작) $q_{0}\in Q$ 0 $q_{0}\in Q$ { $displaystyle q$ _ { $0$ } \ $in$ Q $q_{0}\in Q$ } 。
F $($ 또는 최종) $F\subseteq Q$ 로 구별되는 $F$ 일련의 $상태$ F(\ $displaystyle$ F $F\subseteq Q$

여기서 P $)$ {style { $P}}(Q)$ 는 ${\mathcal {P}}(Q)$ Q $($ displaystyle $Q$ 의 파워셋을 나타냅니다.

인식된 언어

$M=(Q,\Sigma ,\delta ,q_{0},F)$ M $=$ ( $M=(Q,\Sigma ,\delta ,q_{0},F)$ , $M=(Q,\Sigma ,\delta ,q_{0},F)$ 、、 $M=(Q,\Sigma ,\delta ,q_{0},F)$ 、、 $M=(Q,\Sigma ,\delta ,q_{0},F)$ , F ) { $display style$ M = ( Q , \ $Sigma$ , \ signa , q $_ 0$ , F ) $M=(Q,\Sigma ,\delta ,q_{0},F)$ } $L(M)$ display display display 、 displaydisplay 、 $\Sigma$ 、 L ( $L(M)$ ) 、 $displaystyle$ $L(M)$ L $L(M)$ ( M $)$ displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay L ( M )로 정의됩니다.

위의 비공식적인 설명에 느슨하게 대응하여 $w=a_{1}a_{2}...a_{n}$ w $w=a_{1}a_{2}...a_{n}$ $w=a_{1}a_{2}...a_{n}$ $w=a_{1}a_{2}...a_{n}$ $w=a_{1}a_{2}...a_{n}$ 2 $w=a_{1}a_{2}...a_{n}$ . . $w=a_{1}a_{2}...a_{n}$ \ $displaystyle$ w $w=a_{1}a_{2}...a_{n}$ = $a$ _ { $1} a$ _ {2} ...에는 몇 가지 동등한 공식 정의가 있습니다. $a_{n}$ 은 $w=a_{1}a_{2}...a_{n}$ $($ 는) M { $displaystyle$ M $M$ 에 의해 받아들여집니다.

$w$ {\ $displaystyle$ w $}$ 는 $w$ $r_{0},r_{1},...,r_{n}$ 과 같은 일련의 $r_{0},r_{1},...,r_{n}$ r $r_{0},r_{1},...,r_{n}$ $r_{0},r_{1},...,r_{n}$ , $r_{0},r_{1},...,r_{n}$ . . , $r_{0},r_{1},...,r_{n}$ n { $displaystyle$ r $_ 0$ , r _ { $1}$ , $r$ _ $r_{0},r_{1},...,r_{n}$ { n $r_{0},r_{1},...,r_{n}$ 이Q { { $displaystyle$ Q $Q$ } 에 $Q$ 하는 경우 허용됩니다.
1. $r_{0}=q_{0}$
2. $r_{i+1}\in \delta (r_{i},a_{i+1})$ i + $r_{i+1}\in \delta (r_{i},a_{i+1})$ $r_{i+1}\in \delta (r_{i},a_{i+1})$ $r_{i+1}\in \delta (r_{i},a_{i+1})$ , a + 1 $r_{i+1}\in \delta (r_{i},a_{i+1})$ ） { $displaystyle$ r $_$ { $i$ } \ $in \$ display ( $r$ _ { $i$ , a $r_{i+1}\in \delta (r_{i},a_{i+1})$ $i=0,\ldots ,n-1$ { $i$ + $1$ } $r_{i+1}\in \delta (r_{i},a_{i+1})$ 、 $i=0,\ldots ,n-1$ $i=0,\ldots ,n-1$ , $i=0,\ldots ,n-1$ \ $displaystyle$ i = $0$ , \ $ldots$ , n $i=0,\ldots ,n-1$ - 1 $}$ 。
3. $r_{n}\in F$ n $r_{n}\in F$ F { $displaystyle r$ _ { $n$ } $r_{n}\in F$ \ in F 。

즉, 첫 번째 조건은 기계가 시작

q_{0}

q_{0}

0

(\

에서 시작된다는 것입니다.두 번째 조건에서는

string

w {\

displaystyle

w

w

의 각 문자가 지정되면 머신은

\delta

{\

{\

displaystyle \delta

에 따라 상태 간에 이행합니다.마지막 조건에서는 w

{\

displaystyle

w}의

w

마지막

입력으로 인해 m이 발생할 경우 w

{\

displaystyle

w

}

가

w

허용됩니다.accepting 상태 중 하나에서 정지합니다.W

\displaystyle

w가

w

M

displaystyle

M에

의해

허용되기

w

는 모든 상태 시퀀스가 허용 상태로 종료될 필요가 없으며, 허용 상태이면 충분합니다.그렇지 않으면 w

\displaystyle

w

에 따라

w

{

에서

q_0

{displaystyle

F

}

상태로

F

이행하는 것이 전혀 불가능할 경우 오토마톤은 문자열을 거부한다고 합니다.M

(\displaystyle

M

)

에서

M

사용할 수 있는

문자열

세트는

M(\

displaystyle

M

)

에서

M

인식되는 언어이며

L(M)

이 언어는 L

(

)(\

displaystyle

L

(M

^[5]^{: 320}^[6]^{: 54}로

L(M)

됩니다.

$\delta ^{*}(q_{0},w)\cap F\not =\emptyset$ $,$ $\delta ^{*}(q_{0},w)\cap F\not =\emptyset$ 「」( $\delta ^{*}(q_{0},w)\cap F\not =\emptyset$ 0 $\delta ^{*}(q_{0},w)\cap F\not =\emptyset$ w )가 $\delta ^{*}(q_{0},w)\cap F\not =\emptyset$ F $」({displaystyle$ \ $display ^{*})(q_{0},w)\cap$ F\ $not$ =\ $emptyset$ 인 경우 w $\delta ^{*}:Q\times \Sigma ^{*}\rightarrow {\mathcal {P}}(Q)$ $displaystyle$ w $}$ 가 $w$ 받아들여집니다. $\delta ^{*}:Q\times \Sigma ^{*}\rightarrow {\mathcal {P}}(Q)$ 서 $\delta ^{*}:Q\times \Sigma ^{*}\rightarrow {\mathcal {P}}(Q)$ × $\delta ^{*}:Q\times \Sigma ^{*}\rightarrow {\mathcal {P}}(Q)$ $Q)$ \ $style$ \display $^*)$ $Q\times$ \ $Sigma ^{*}\rightarrow {mathcal {P}}(Q)}$ 는 $\delta ^{*}:Q\times \Sigma ^{*}\rightarrow {\mathcal {P}}(Q)$ 다음과 같이 재귀적으로 정의됩니다.
1. $\delta ^{*}(r,\epsilon )=\{r\}$ $"$ $\delta ^{*}(r,\epsilon )=\{r\}$ "r" $=$ { $r$ }({ $displaystyle$ \displaystyle $^{*}(r,\ilon)=\{$ r $\delta ^{*}(r,\epsilon )=\{r\}$ \}) $여기서$ "\ $displaystyle$ \ilon }은 $\epsilon$ 빈 문자열입니다 $\epsilon$ .
2. $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ $x\in \Sigma ^{*},a\in \Sigma$ A에 $x\in \Sigma ^{*},a\in \Sigma$ $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ a $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ $=$ $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ r $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ ( $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ , x ) $r$ , $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ a $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ ){ $displaystyle$ \ displaystyle ^ { * } ( r , $xa$ )=\ $bigcup$ _ { $r$ ' \ $in$ \ $in$ \ r * * * $}$ ( r , x ) $}$ \ $display$ cup $（$ r , a $\delta ^{*}(r,xa)=\bigcup _{r'\in \delta ^{*}(r,x)}\delta (r',a)$ ) $x\in \Sigma ^{*},a\in \Sigma$

\delta ^{*}(r,x)

state

\delta ^{*}(r,x)

r {\

displaystyle

\

delta ^{*}(r,x

)}은

\delta ^{*}(r,x)

문자열

x

{\

displaystyle

x

x

를 소비함으로써 상태 r

{\

displaystyle

r

}

에서

r

도달 가능한 모든 상태의 집합입니다.

문자열

w

\displaystyle

w}는

w

^[4]^{: 21}^[7]^{: 59}w

\displaystyle

w를

w

으로써

F\

displaystyle

F의

F

일부

허용 상태에 시작

q_{0}

q_{0}

0(\

displaystyle q_{

0

q_{0}

})에서

w

도달할 수 있는 경우에 사용할 수 있습니다.

초기 상태

위의 자동 정의에서는 단일 초기 상태를 사용하며, 이는 필요하지 않습니다.NFA는 초기 상태 세트로 정의되는 경우가 있습니다.여러 초기 상태를 가진 NFA를 단일 초기 상태를 가진 NFA로 변환하는 간단한 구성이 있으며, 이를 통해 편리한 표기가 제공됩니다.

예

M의 상태 다이어그램.상태 p에서 1을 읽으면 p 또는 q로 이어질 수 있으므로 확정적이지 않습니다.	입력 문자열 "10"에서 가능한 모든 M 실행.
입력 문자열 "1011"에서 가능한 모든 M 실행. 호 레이블: 입력 기호, 노드 레이블: 상태, 녹색: 시작 상태, 빨간색: 수락 상태.

$M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ 자동 $($ 이진 $알파벳$ 포함)은 입력이 $M$ 1로 끝나는지 여부를 결정합니다. M = ( { p $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ , $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ , { $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ , $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ , " $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ , $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ , { q $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ ) { $displaystyle$ M $=$ ( \ { p , $q$ \ , \ { $0$ , $1$ \ , \ , \ $deltap$ , { $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ } ) $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ } ) $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ 여기서 전환은 $\delta$ 합니다 $M=(\{p,q\},\{0,1\},\delta ,p,\{q\})$ .왼쪽 위 그림):

입력 주	0	1
$p$	${\displaystyle\{p\}}$	${\displaystyle\{p,q\}}$
$q$	$\displaystyle \emptyset }$	$\displaystyle \emptyset }$

$\delta (p,1)$ $\delta (p,1)$ ( $\delta (p,1)$ , $\delta (p,1)$ ) { $displaystyle \delta ($ p , $1$ ) 에는 $\delta (p,1)$ 복수의 상태가 포함되어 있기 $M$ 에 M{ $displaystyle$ M}은 $M$ 확정적이지 않습니다.M $(\displaystyle$ M $)$ 의 $M$ 언어는 정규 표현에서 주어진 정규 언어로 설명할 수 있습니다. (0 1)*1.

입력 문자열 "1011"에 대해 가능한 모든 상태 시퀀스가 아래 그림에 표시됩니다.하나의 상태 시퀀스가 위의 정의를 충족하기 때문에 문자열은 M{\ $displaystyle$ M $}$ 에 $M$ 의해 받아들여집니다.다른 시퀀스가 실패해도 상관없습니다.이 그림은 두 가지 방법으로 해석할 수 있습니다.

위의 "lucky-run" 설명과 관련하여, 그림의 각 경로는 M $\display style$ 의 선택 순서를 나타냅니다.
"복제" 설명의 경우, 각 세로 열은 특정 시점에 $M의$ 클론을 나타내며, 노드에서 나오는 여러 개의 화살표는 복제를 나타내며, "복제"를 나타내는 화살표가 없는 노드는 클론의 죽음을 나타냅니다.

같은 그림을 두 가지 방법으로 읽을 수 있는 가능성은 위의 두 가지 설명의 동등성을 나타낸다.

위의 공식 정의 중 첫 번째를 고려할 때 "1011"은 M {\ $displaystyle$ M $}$ 이 $M$ $($ 가 $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ 시퀀스 $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ , $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ , $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ , r 3, r 4 $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ ⟨ $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ , $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ , $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ q $\langle r_{0},r_{1},r_{2},r_{3},r_{4}\rangle =\langle p,p,p,p,q\rangle$ {\ { \ $display$ \ displayle $r _$ 0 , r _ $0$ , r _ 1 , r _ r _ $r$ _ 4 $}$ 를 $M$ 할 수 있기 때문에 허용됩니다.tions 1 ~3 。
두 번째 공식 정의에 대해 상향식 계산에서는 $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ $\delta ^{*}(p,\epsilon )=\{p\}$ ( p , $\delta ^{*}(p,\epsilon )=\{p\}$ ) $\delta ^{*}(p,\epsilon )=\{p\}$ { $\delta ^{*}(p,\epsilon )=\{p\}$ $\delta ^{*}(p,\epsilon )=\{p\}$ ( \ $displaystyle$ \ $display$ ^ { * （ $p$ , \ $silon$ ） $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ \ { p \ $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ $\delta ^{*}(p,\epsilon )=\{p\}$ ( $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ , $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ ) $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ ( $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ , $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ ) $=$ { $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ , $\delta ^{*}(p,1)=\delta (p,1)=\{p,q\}$ 、 { p $,$ ( \ $display style$ \ ^ { p } ) （ 1 、 p $}$ ( $1$ ) $ystyle \display ^{*}(p,$ $10$ $)=\display$ ( $p,$ $\delta ^{*}(p,101)=\delta (p,1)=\{p,q\}$ $)\cup \display$ ( $\delta ^{*}(p,101)=\delta (p,1)=\{p,q\}$ $,0$ )=\{ $p$ $\}\$ $cup$ $\{\$ cup \{\cup $\delta ^{*}(p,10)=\delta (p,0)\cup \delta (q,0)=\{p\}\cup \{\}$ $\delta ^{*}(p,101)=\delta (p,1)=\{p,q\}$ "" ( $,$ $=$ "" (p,101) $\delta ^{*}(p,101)=\delta (p,1)=\{p,q\}$ { $, }$ { $display$ \display $^{*}$ ( $p,101$ ) $\delta ^{*}(p,1011)=\delta (p,1)\cup \delta (q,1)=\{p,q\}\cup \{\}$ 이 세트는 { $}$ { $displaystyle \{q$ 에서 분리되지 않으므로 문자열 "1011"이 허용됩니다.

반면 문자열 "10"은 마지막 0 기호를 읽는 것으로 유일한 허용 $상태$ q { $displaystyle$ q $q$ 에 도달할 수 없기 때문에 M{ $displaystyle$ M $}$ 에 $의해$ 거부됩니다(그 입력에 대해 가능한 모든 상태 시퀀스가 오른쪽 상단에 표시됩니다).첫번째 "1"을 $소비$ 한 후q\displaystyle q에 $q$ 도달할 수 $있지만$ , 이는 입력 "10"을 받아들이는 것이 아니라 입력 문자열 "1"을 받아들이는 것을 의미합니다.

DFA와의 동등성

결정론적 유한 오토마톤(DFA)은 각 상태와 심볼에 대해 전이 함수가 정확히 하나의 상태를 갖는 특수한 종류의 NFA로 볼 수 있다.따라서, DFA에 의해 인정될 수 있는 모든 공식 언어가 NFA에 의해 인정될 수 있다는 것은 분명하다.

반대로 각 NFA에는 동일한 공식 언어를 인식할 수 있는 DFA가 있습니다.DFA는 파워셋 구조를 사용하여 구성할 수 있습니다.

이 결과는 NFA가 추가적인 유연성에도 불구하고 일부 DFA에서 인식할 수 없는 언어를 인식할 수 없음을 보여준다.구축이 용이한 NFA를 보다 효율적으로 실행 가능한 DFA로 변환하는 것도 실무에서 중요하다.단, NFA가 n개의 상태를 갖는 경우 결과 DFA는 $2^{n}$ $(\$ })의 상태를 가질 수 있으며, 이로 인해 대규모 NFA에서는 구축이 실용적이지 않을 수 있습니다.

µ-moves가 있는 NFA

γ-moves(NFA-)를 갖는 비결정론적 유한 오토마톤은 NFA에 대한 추가적인 일반화이다.이러한 오토마톤에서는 빈 문자열θ에 전이함수를 추가 정의한다.입력 기호를 소비하지 않는 천이를 θ-트랜지션이라고 하며 상태 다이어그램에 "θ"라는 화살표로 나타냅니다. θ-트랜지션은 현재 상태를 정확하게 알 수 없는 시스템을 모델링하는 편리한 방법을 제공합니다. 즉, 시스템을 모델링하고 현재 상태(입력 처리 후)가 명확하지 않은 경우string)은 q 또는 q'이어야 합니다.그러면 이 두 상태 사이에 '트랜지션'을 추가할 수 있기 때문에 자동화가 동시에 두 상태에 놓입니다.

형식적 정의

NFA-tuple은 5개의 태플 $(Q$ $0, F$ 로 정식으로 표현되며 다음과 같이 $구성$ 됩니다.

$유한$ 상태 Q $(\displaystyle$ Q $)$
알파벳 $\Sigma$ (\ $displaystyle \Sigma)$ 라고 하는 입력 기호 집합
전이 함수 $\delta :Q\times (\Sigma \cup \{\epsilon \})\rightarrow {\mathcal {P}}(Q)$ : $\delta :Q\times (\Sigma \cup \{\epsilon \})\rightarrow {\mathcal {P}}(Q)$ × ( $\delta :Q\times (\Sigma \cup \{\epsilon \})\rightarrow {\mathcal {P}}(Q)$ { $\delta :Q\times (\Sigma \cup \{\epsilon \})\rightarrow {\mathcal {P}}(Q)$ } ) $\delta :Q\times (\Sigma \cup \{\epsilon \})\rightarrow {\mathcal {P}}(Q)$ ( $\delta :Q\times (\Sigma \cup \{\epsilon \})\rightarrow {\mathcal {P}}(Q)$ Q ) $\delta :Q\times (\Sigma \cup \{\epsilon \})\rightarrow {\mathcal {P}}(Q)$ \ $displaystyle$ \ $display :$ $Q\times (\Sigma \cup \{\epsilon \})\rightarrow {Mathcal {P}}(Q)}$
초기(또는 시작) $q_{0}\in Q$ $q_{0}\in Q$ $†$ Q { $displaystyle q$ _ { 0 $q_{0}\in Q$ } \ $in$ Q }
F $($ 또는 최종) $F\subseteq Q$ 로 구별되는 $F$ 일련의 $상태$ F(\ $displaystyle$ F $F\subseteq Q$

여기서 P $)$ { $style{mathcal$ {P $}}($ $Q)}$ 은 ${\mathcal {P}}(Q)$ Q $(\displaystyle$ Q)의 $Q$ 파워셋을 나타내고 denotes는 빈 문자열을 나타냅니다.

상태 또는 상태 집합의 폐쇄

$상태 Q$ 의 $q\in Q$ 경우 $q\in Q$ E $(q)$ 는 트랜지션 함수 $\delta$ 의 트랜지션 $(\displaystyle \delta$ 즉 $p\in E(q)$ ( $)가 존재$ 하는 $E(q)$ $q$ $p\in E(q)$ 경우 $q$ 에서 도달 가능한 상태 세트를 $나타냅니다$ $.$ $q_{1},...,q_{k}$ , $q_{1},...,q_{k}$ . . $q_{1},...,q_{k}$ , $q_{1},...,q_{k}$ k ( \ $display style q _$ {1} , , $q _$ { k $q_{1},...,q_{k}$ } )이렇게 되어 있습니다.

$q_{1}=q$ 1 $q_{1}=q$ q { $displaystyle q$ _ {1} $=$ q $q_{1}=q$ } ,
$q_{i+1}\in \delta (q_{i},\varepsilon )$ for each $1\leq i<k$ , and
$q_{k}=p$ k $q_{k}=p$ { $displaystyle q$ _ {k } = $p$ } 。

$E(q)$ { $displaystyle$ E $(q)}$ 는 $E(q)$ $q$ {displaystyleq $q$ 의 엡실론 폐쇄('-closure'라고도 합니다.

NFA 상태의 $집합$ P(\ $displaystyle$ P $)$ 의 $P$ 폐쇄는 전환 후에 P $(\displaystyle$ P) 내의 $P$ $모든$ 상태에서 도달 가능한 상태의 집합으로 정의됩니다.정식으로 P $P\subseteq Q$ Q $P\subseteq Q$ \ $displaystyle$ P \ $subseteq$ 에 $E(P)=\bigcup \limits _{q\in P}E(q)$ E $E(P)=\bigcup \limits _{q\in P}E(q)$ ( $E(P)=\bigcup \limits _{q\in P}E(q)$ ) $=$ q $display$ P E ( q ) \ $displaystyle$ E ( P ) $=$ \ $big$ cup \ $big$ cup _ ${ q$ \ $in$ P }E $($ )를 정의합니다.

확장 전환 기능

"-moves"가 없는 NFA와 마찬가지로 NFA-"의 전이 함수 $"\displaystyle\delta"$ 를 $\delta$ 문자열로 확장할 수 있습니다.비공식적으로 $\delta ^{*}(q,w)$ $\delta ^{*}(q,w)$ \ $^^{*}(q,w)}$ 는 $\delta ^{*}(q,w)$ $w\in \Sigma ^{*}.$ $상태Q$ 에서 $q\in Q$ 시작하여 $w\in \Sigma ^{*}.$ 를 $w\in \Sigma ^{*}.$ 읽었을 때 자동이 도달했을 가능성이 있는 모든 상태의 집합을 나타냅니다 $.{$ $displaystyle$ $q\in Q$ w $\in \Sigma$ $q\in Q$ $^$ { * } } 。 $\delta ^{*}:Q\times \Sigma ^{*}\rightarrow {\mathcal {P}}(Q)$ ${*}: Q\times \Sigma ^{*}\rightarrow {mathcal {P}}(Q)}$ 는 $\delta ^{*}:Q\times \Sigma ^{*}\rightarrow {\mathcal {P}}(Q)$ 다음과 같이 재귀적으로 정의할 수 있습니다.

$\delta ^{*}(q,\varepsilon )=E(q)$ $q\in Q,$ $\delta ^{*}(q,\varepsilon )=E(q)$ \ $displaystyle q,$ \displaystyle $q$ $q\in Q,$ $varepsilon)=E$ $($ q $\delta ^{*}(q,\varepsilon )=E(q)$ $각$ 상태 Q $,\displaystyle q$ ,\ $in$ Q,\ $displaystyle$ E는 $E$ 엡실론 폐쇄를 나타냅니다.

비공식: 빈 문자열을 읽으면 q

.\

displaystyle

q

q

.\displaystyle

q

.\

displaystyle q.의 엡실론 닫힘 상태가 될 수 있습니다.

${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ $,$ ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ a ) ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ $q\in Q,$ ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ ) ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ E ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ ( $r$ , a ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ ) 、 { ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ $textstyle$ \ $display$ ^ { * （ ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ q , w ） = \ $bigcup _$ { $r$ \ $in$ \ display $q\in Q,$ $^$ { * $（ q$ , w ） } $q\in Q,$ ${\textstyle \delta ^{*}(q,wa)=\bigcup _{r\in \delta ^{*}(q,w)}E(\delta (r,a)),}$ ( \ $delta$ ) 。

비공식적으로

:

w

를

w

읽으면 재귀적으로 계산된 집합

\delta ^{*}(q,w)

( (

\delta ^{*}(q,w)

,

\delta ^{*}(q,w)

w )의

q

상태

\delta ^{*}(q,w)

r

에서

상태

r (

q

, w )로 자동화할 수 있습니다.그 후, \

displaystyle

^{*

}

(q ,

w

)를 읽으면, \

displaystyle

a가

a

r

할 수 있습니다

.

tyle

r

}

을

r

(를

\delta (r,a).

닫힘의 임의의 상태로 만듭니다

.\

displaystyle \ displaystyle

(

r

,

\delta (r,a).

)

\delta (r,a).

。

}

자동화는 다음과 같은 경우 w $\displaystyle$ w $w$ 을 $w$ 수신할 수 있습니다.

\displaystyle \delta ^{*}(q_{0},w)\cap F\neq \emptyset ,}

즉, w $.\displaystyle$ 을 $w$ $w$ 하여 읽으면 자동이 $q_{0}$ 상태 $q_{0}$ .\ $displaystyle q_{$ 0 $q_{0}$ $}$ 에서 $F$ .\ $displaystyle$ F의 허용 상태로 구동됩니다. $}$ ^[4]^{: 25}

예

M의 상태 다이어그램

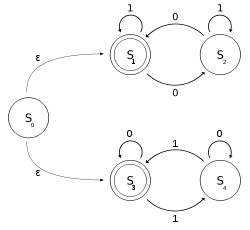
M(\ $displaystyle$ M $)$ 을 $M$ 2진수 알파벳을 사용하여 짝수 0 또는 짝수 1 중 어느 것을 입력에 포함시킬지 결정하는 NFA-θ로 $합니다$ .0 오카렌스는 짝수 오카렌스이기도 합니다.

$M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ 표기법에서는 M $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ ( $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ { $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ 0 , $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ 1, S $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , S $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , { $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ 0 $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , { $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ , $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ ) $M=(\{S_{0},S_{1},S_{2},S_{3},S_{4}\},\{0,1\},\delta ,S_{0},\{S_{1},S_{3}\})$ { $displaystyle$ M = ( \ { $S _ 0$ , $S _$ { 1 , S _ $2 }$ , S _ { $4 }$ ) 。

입력 주	0	1	ε
S₀	{}	{}	{S₁, S₃}
S₁	{S₂}	{S₁}	{}
S₂	{S₁}	{S₂}	{}
S₃	{S₃}	{S₄}	{}
S₄	{S₄}	{S₃}	{}

$({displaystyle$ M $})$ 은 $M$ $\{S_{1},S_{2}\}$ 2개의 DFA의 $\{S_{1},S_{2}\}$ 결합으로 $\{S_{1},S_{2}\}$ 볼 수 있습니다.하나는 $\{S_{1},S_{2}\}$ 가 { $S1,$ ${1}, S_{2}\}$ 이고 다른 $\{S_{1},S_{2}\}$ 하나는 상태가 $\{S_{3},S_{4}\}$ { $\{S_{3},S_{4}\}$ $S4}{displaystyle$ \{ $3}, S_4$ 입니다. $M의$ (\ $displaystyle$ M $)$ 는 $M$ 이 정규 $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ 1 $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ 0 1 $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ 0 ) $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ ( $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ 10 $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ 1) ${\$ ( \ $display$ style ( $1$ ^ * ) $01$ ^ { * 0 $)^*}\cup$ ( $0$ ^ { * } $10$ $M$ $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ ^ { * 1 $)^$ * )^* $(1^{*}01^{*}0)^{*}\cup (0^{*}10^{*}1)^{*}$ } } 。 $디스플레이 M$ 을 사용하여 $M$ 합니다.「-」를 사용해 출력합니다.

NFA와의 동등성

NFA-θ가 NFA와 동등함을 나타내기 위해 먼저 NFA는 NFA-θ의 특수한 경우이므로 모든 NFA-θ에 대해 동등한 NFA가 존재함을 보여 줍니다.

엡실론이 $M=(Q,\Sigma ,\delta ,q_{0},F),$ $M=(Q,\Sigma ,\delta ,q_{0},F),$ ( $M=(Q,\Sigma ,\delta ,q_{0},F),$ , $M=(Q,\Sigma ,\delta ,q_{0},F),$ , $M=(Q,\Sigma ,\delta ,q_{0},F),$ , $M=(Q,\Sigma ,\delta ,q_{0},F),$ ) , $M=(Q,\Sigma ,\delta ,q_{0},F),$ { $displaystyle$ M = ( Q , \ $Sigma$ , \ $sigma$ , \ $sigma$ , q _ { $0$ , F $M=(Q,\Sigma ,\delta ,q_{0},F),$ } )인 $M=(Q,\Sigma ,\delta ,q_{0},F),$ NFA는 $M'=(Q,\Sigma ,\delta ',q_{0},F'),$ M $M'=(Q,\Sigma ,\delta ',q_{0},F'),$ ( $M'=(Q,\Sigma ,\delta ',q_{0},F'),$ , 、 $M'=(Q,\Sigma ,\delta ',q_{0},F'),$ 、 $M'=(Q,\Sigma ,\delta ',q_{0},F'),$ , 0 $M'=(Q,\Sigma ,\delta ',q_{0},F'),$ , )를 정의합니다 $.$

F'={case} 시작F\cup \{q_{0}\}&{\text{if}}E(q_{0})\cap F\neq \{\}\\\F&{\text{그렇지 않으면}}\\end{case}

그리고.

\delta '(q,a)=\delta ^{*}(q,a)

,

\delta '(q,a)=\delta ^{*}(q,a)

a )

\delta '(q,a)=\delta ^{*}(q,a)

q

, a

\delta '(q,a)=\delta ^{*}(q,a)

)

\delta '(q,a)=\delta ^{*}(q,a)

\delta '(q,a)=\delta ^{*}(q,a)

∗

display

、

∗

display

、

Q

q\in Q

、 \

\delta '(q,a)=\delta ^{*}(q,a)

displaystyle

=

\

sigma

a\in \Sigma ,

} 、

a\in \Sigma ,

q\in Q

a\in \Sigma ,

、 ∗

\delta ^{*}

、 \

displaystyle

a \

sigma

\delta ^{*}

。

M $(디스플레이 스타일)$ 과 $M$ $M ($ 디스플레이 $스타일)$ 의 전환 기능을 $M',$ $M$ 해야 합니다 $.$ $\delta$ $string$ 에 대한 $\delta$ 확장자는 $\delta$ $각각$ $\delta$ ${\$ $displaystyle$ $\displaystyle$ $\$ $displaystyle\$ displaystyle $\delta ',$ $\delta$ \displaystyle $\delta '^{*},$ \displaystyle $'^{*}, 입니다.$ By construction, $M'$ has no ε-transitions.

$wstyle$ 의 길이에 $따라$ $\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)$ $w\neq \varepsilon$ w에 대해 $w\neq \varepsilon$ q $\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)$ ) $\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)$ 0 $\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)$ ) $\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)$ = display $^{*}(q_{0,w$ = \ $display$ $\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)$ $style$ w $\$ $neq \varepsilon$ 인덕션으로 $\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)$ 할 수 있습니다 $.$

이를 바탕으로 $\delta '^{*}(q_{0},w)\cap F'\neq \{\}$ $displaystyle \delta `^{*}(q_{0},$ w)\ $cap$ F'\ $neq \{\}$ 이 $\delta '^{*}(q_{0},w)\cap F'\neq \{\}$ ( $\delta ^{*}(q_{0},w)\cap F\neq \{\},$ ) $\delta ^{*}(q_{0},w)\cap F\neq \{\},$ ( $\delta '^{*}(q_{0},w)\cap F'\neq \{\}$ 0 $\delta ^{*}(q_{0},w)\cap F\neq \{\},$ $\delta '^{*}(q_{0},w)\cap F'\neq \{\}$ $\delta ^{*}(q_{0},w)\cap F\neq \{\},$ F $\delta ^{*}(q_{0},w)\cap F\neq \{\},$ {\ $ta$ style $^{\$ ta $\delta '^{*}(q_{0},w)\cap F'\neq \{\}$ $임$ 을 표시할 수 있습니다 $.$

w $w=\varepsilon ,$ 、 { $displaystyle$ w = \ $varepsilon$ $}$ 인 경우 이는 F $′$ . { $displaystyle$ F $'$ 의 $F'.$ 에 따릅니다. $}$
그렇지 않으면 $w=va$ $w=va$ $w=va$ v a $w=va$ {\ $displaystyle w=$ va $w=va$ $}$ ( $v\in \Sigma ^{*}$ $v\in \Sigma ^{*}$ \ $displaystyle$ v \ $in$ \ Sigma $^$ { * } ) $a\in \Sigma .$ . \ $displaystyle$ a \ $in$ \ Sigma $a\in \Sigma .$ } 로 $w=va$ 합니다.

\delta '^{*}(q_{0},w)\cap F'\neq \{\}\;\Leftarrow \;\delta ^{*}(q_{0},w)\cap F\neq \{\};

\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)

0

\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)

)

\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)

0, w )

=

q 0

\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)

) =\

display

style \

display '^{*}(q_{0},

w) =\

display ^{*}(q_{0},w)

} 및

\delta '^{*}(q_{0},w)=\delta ^{*}(q_{0},w)

F\subseteq F',

F\subseteq F',

F\subseteq F',

⊆

F\subseteq F',

{

displaystyle

F

\subseteq

'

\delta '^{*}(q_{0},w)\cap F'\neq \{\}\;\Leftarrow \;\delta ^{*}(q_{0},w)\cap F\neq \{\};

\delta '^{*}(q_{0},w)\cap F'\neq \{\}\;\Leftarrow \;\delta ^{*}(q_{0},w)\cap F\neq \{\};

\delta '^{*}(q_{0},w)\cap F'\neq \{\}\;\Leftarrow \;\delta ^{*}(q_{0},w)\cap F\neq \{\};

\delta '^{*}(q_{0},w)\cap F'\neq \{\}\;\Leftarrow \;\delta ^{*}(q_{0},w)\cap F\neq \{\};

。

^{*}(q_{0},w)\cap

F

\neq \{\};}

그래도

\delta '^{*}(q_{0},w)\cap F'\neq \{\}\;\Leftarrow \;\delta ^{*}(q_{0},w)\cap F\neq \{\};

"\displaystyle \Rightarrow

방향을 표시해야 합니다.

$\delta '^{*}(q_{0},w)$ 0 $\delta '^{*}(q_{0},w)$ ) { $displaystyle \delta '^{*}(q_{0},w$ $\delta ^{*}(q_{0},w)$ 이 $\delta '^{*}(q_{0},w)$ (가) $F'\setminus \{q_{0}\},$ $F'\setminus \{q_{0}\},$ { $F'\setminus \{q_{0}\},$ $\delta ^{*}(q_{0},w)$ $F'\setminus \{q_{0}\},$ { $displaystyle$ F $'\setminus$ \{ $q_{0}\},$ { $displaystyle \delta ^{0}$ 의 $F'\setminus \{q_{0}\},$ $\delta ^{*}(q_{0},w)$ 상태일 경우 { $\delta ^{*}(q_{0},w)$ 이 $($ 가)를 포함합니다.
$\delta '^{*}(q_{0},w)$ 0 $\delta '^{*}(q_{0},w)$ ) {{ $displaystyle$ \ $delta '^{$ 0}( $q_{0},$ $\delta ^{*}(q_{0},w)$ $)}$ 이 $\delta '^{*}(q_{0},w)$ ( $q_{0},$ ) q $q_{0},$ 0 $,$ { $0}$ $및$ $q_{0}\in F,$ 0 $\delta ^{*}(q_{0},w)$ $q_{0}\in F,$ F $,$ { $displaystyle q_$ ${0$ }\ $in$ F $,$ { $displaystyle \delta$ ^*}( $0)$ 을 $q_{0},$ 하는 경우 $\delta ^{*}(q_{0},w)$ 도 $q_{0}\in F,$ $\delta ^{*}(q_{0},w)$ 포함됩니다 $.$ $q_{0}.$ $}$
만약 δ∗(q0, w){\displaystyle\delta '^{*}(q_{0}일 경우 ,w)′}}그때 E(q0)∩ F{\displaystyle E(q_{0})\cap F}[ 밝히다]의 상태에 있어야 합니다 0,{\displaystyle q_{0},}과qq 0∉ F,{\displaystyle q_{0}\not \in F,가 들어 있δ ∗(q0, w))⋃ r∈ δ ∗(q, v)E(δ(r,.a)). $\textstyle \delta ^{*}(q_{0},w)=\bigcup _{r\in \delta ^{*}(q,v)}E(\delta(r,a))$ $}$ ^[4]^{: 26–27}

NFA는 DFA와 같기 때문에 NFA-γ도 DFA와 같다.

닫힘 속성

특정 NFA N(s) 및 N(t)의 언어 조합을 받아들이는 NFA 구성.언어연합의 입력문자열 w에 대해 합성오토마톤은 적절한 서브오토마톤(N(s) 또는 N(t))의 시작상태(좌측색원)로의 θ-전이를 따르며, w에 따라 허용상태(우측색원)에 도달하면 다른 θ-전이에 의해 상태 f에 도달할 수 있다.γ-변화에 의해 N(s)과 N(t)이 모두 DFA라고 해도 구성 NFA는 결정적이지 않다.반대로, 조합 언어(DFA 2개라도)의 DFA를 구축하는 것은 훨씬 복잡하다.

NFA에 의해 인식된 언어 세트는 다음 조작으로 닫힙니다.이러한 폐쇄 연산은 정규식으로 NFA를 구성하는 Thompson의 구성 알고리즘에서 사용됩니다.또한 NFA가 정규 언어를 정확하게 인식한다는 것을 증명하기 위해 사용될 수 있다.

Union(그림 참조), 즉 언어₁ L이 일부 NFA A₁ 및 일부₂ A에₂ 의해 받아들여지면 언어₁ L∪L을₂ 받아들이는 NFA_u A를 구축할 수 있다.
교집합. 마찬가지로 A와₂₂ A에서₁ LfaL을_i₁ 받아들이는 NFA A를 구성할 수 있다.
연결
부정. 마찬가지로 A에서₁ δ^*\L을₁ 받아들이는 NFA_n A를 구성할 수 있습니다.
클린 클로저

NFA는 γ-moves(NFA-θ)를 갖는 비결정론적 유한 오토마톤에 해당하므로 위의 폐색성은 NFA-θ의 폐색 특성을 사용하여 증명된다.

특성.

시스템은 지정된 초기 상태에서 시작하여 알파벳에서 일련의 기호를 읽습니다.자동화는 상태 전이 함수 δ를 사용하여 현재 상태를 사용하여 다음 상태를 판별합니다.기호는 방금 읽었거나 빈 문자열입니다.단, NFA의 다음 상태는 현재 입력 이벤트뿐만 아니라 임의의 수의 후속 입력 이벤트에 따라 달라집니다.이러한 후속 이벤트가 발생할 때까지 기계가 어떤 상태인지 판단할 수 없습니다."^[8]자동화가 판독을 종료했을 때, NFA는 문자열을 받아들인다고 하고, 그렇지 않으면 문자열을 거부한다고 합니다.

NFA가 받아들이는 모든 문자열의 집합은 NFA가 받아들이는 언어입니다.이 언어는 정규 언어입니다.

모든 NFA에 대해 동일한 언어를 받아들이는 결정론적 유한 오토마톤(DFA)을 찾을 수 있습니다.따라서 (아마도) 더 단순한 머신을 구현하기 위해 기존 NFA를 DFA로 변환할 수 있습니다.이는 파워셋 구조를 사용하여 수행할 수 있으며, 이로 인해 필요한 상태의 수가 기하급수적으로 증가할 수 있습니다.파워셋 구성에 대한 공식적인 증거는 파워셋 구성 문서를 참조하십시오.

실행

NFA를 실장하는 방법에는 여러 가지가 있습니다.

동등한 DFA로 변환합니다.경우에 따라서는, 이 때문에,^[9] 상태수가 기하급수적으로 증가하는 일이 있습니다.
NFA가 현재 있을 수 있는 모든 상태의 데이터 구조를 유지합니다.입력 심볼을 사용할 때 모든 현재 상태에 적용되는 전환 함수의 결과를 통합하여 다음 상태 집합을 가져옵니다. "-move"가 허용될 경우 이러한 이동("-closure")에 의해 도달 가능한 모든 상태를 포함합니다.각 단계에는 최대 계산²(s는 NFA의 상태 수)이 필요합니다.마지막 입력 기호를 사용할 때 현재 상태 중 하나가 최종 상태일 경우 기계는 문자열을 받아들입니다.길이 n의 ^[7]^{: 153}문자열은 시간 O(ns²) 및 공간 O(s)로 처리할 수 있다.
여러 복사본을 만듭니다.NFA는 각 n방향 결정에 대해 $(\displaystyle n-1)$ 의 $n-1$ 기계 복사본을 생성합니다.각각 다른 상태가 됩니다.마지막 입력 기호를 소비할 때 NFA의 복사본이 하나 이상 수락 상태에 있는 경우 NFA는 수락합니다.(각 NFA 상태에 대해 1대의 머신이 존재할 수 있기 때문에 이 경우에도 NFA 상태의 수에 관한 리니어 스토리지가 필요합니다).
NFA의 트랜지션 구조를 통해 토큰을 명시적으로 전파하고 토큰이 최종 상태에 도달할 때마다 일치시킵니다.이것은 NFA가 이행을 트리거한 이벤트에 대한 추가 컨텍스트를 인코딩해야 할 때 도움이 될 수 있습니다(이 기술을 사용하여 객체 참조를 추적하는 구현의 경우 Tracematches를 참조하십시오).^[10]
PSPACE-complete는 NFA가 지정된 경우 범용인지, ^[11]즉 NFA가 수용하지 않는 문자열이 있는지 테스트합니다.포함 문제에서도 마찬가지다. 즉, 두 개의 NFA가 주어진 경우, 하나의 언어가 다른 언어의 하위 집합이다.

NFA 적용

NFA와 DFA는 언어가 NFA에 의해 인식되면 DFA에 의해 인식된다는 점에서 동등합니다.그러한 동등성의 확립은 중요하고 유용하다.특정 언어를 인식하기 위해 NFA를 작성하는 것이 해당 언어에 대한 DFA를 작성하는 것보다 훨씬 쉬울 수 있기 때문에 유용합니다.NFA는 계산 이론에서 많은 중요한 속성을 확립하기 위해 필요한 수학적 작업의 복잡성을 줄이기 위해 사용될 수 있기 때문에 중요하다.예를 들어, DFA보다 NFA를 사용하여 정규 언어의 폐쇄 특성을 증명하는 것이 훨씬 쉽습니다.

「」를 참조해 주세요.

메모들

^ Martin, John (2010). Introduction to Languages and the Theory of Computation. McGraw Hill. p. 108. ISBN 978-0071289429.
^ Rabin, M. O.; Scott, D. (April 1959). "Finite Automata and Their Decision Problems". IBM Journal of Research and Development. 3 (2): 114–125. doi:10.1147/rd.32.0114.
^ 선택 시퀀스는 현재 입력 기호에 적용할 수 있는 전환이 없는 "막다른 골목"으로 이어질 수 있습니다. 이 경우 성공하지 못한 것으로 간주됩니다.
^ ^a ^b ^c ^d ^e John E. Hopcroft and Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Reading/MA: Addison-Wesley. ISBN 0-201-02988-X.
^ ^a ^b Alfred V. Aho and John E. Hopcroft and Jeffrey D. Ullman (1974). The Design and Analysis of Computer Algorithms. Reading/MA: Addison-Wesley. ISBN 0-201-00029-6.
^ ^a ^b Michael Sipser (1997). Introduction to the Theory of Computation. Boston/MA: PWS Publishing Co. ISBN 0-534-94728-X.
^ ^a ^b ^c John E. Hopcroft and Rajeev Motwani and Jeffrey D. Ullman (2003). Introduction to Automata Theory, Languages, and Computation (PDF). Upper Saddle River/NJ: Addison Wesley. ISBN 0-201-44124-1.
^ FOLDOC 무료 온라인 컴퓨팅 사전 유한 상태 기계
^ http://cseweb.ucsd.edu/~ccalabro/fsa.pdf^{[베어 URL PDF]}
^ Alan, C., Avgustinov, P., Christensen, A. S., Hendren, L., Kuzins, S., Lotak, O., de Moor, O., Sereni, D., Sittampalam, G. 및 Tible, 2005.Wayback Machine에서 AspectJ Archived 2009-09-18에 자유 변수를 사용한 트레이스 매칭을 추가합니다.오브젝트 지향 프로그래밍, 시스템, 언어 및 애플리케이션에 관한 제20회 ACM SIGPLAN 회의의 속행(2005년 10월 16일~20일)OPSLA '05년ACM, 뉴욕, 뉴욕, 345-364
^ 이력: 최신 프레젠테이션에 대해서는 [1]을 참조해 주세요.

레퍼런스

M.O. 라빈과 D.Scott, "Finite Automata and the Decision Problems", IBM Journal of Research and Development, 3:2(1959) 페이지 115–125.
마이클 십서, 계산 이론 입문보스턴, PWS.1997. ISBN 0-534-94728-X. (섹션 1.2: 비결정론, 페이지 47-63 참조).
존 E. 홉크로프트와 제프리 D.Ulman, 자동타 이론, 언어, 계산 입문, Adison-Wesley Publishing, Reading Massachusetts, 1979.ISBN 0-201-02988-X. (2장 참조)

[1] Martin, John (2010). Introduction to Languages and the Theory of Computation. McGraw Hill. p. 108. ISBN 978-0071289429.

[2] Rabin, M. O.; Scott, D. (April 1959). "Finite Automata and Their Decision Problems". IBM Journal of Research and Development. 3 (2): 114–125. doi:10.1147/rd.32.0114.

[3] 선택 시퀀스는 현재 입력 기호에 적용할 수 있는 전환이 없는 "막다른 골목"으로 이어질 수 있습니다. 이 경우 성공하지 못한 것으로 간주됩니다.

[Hopcroft.Ullman.1979-4] John E. Hopcroft and Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Reading/MA: Addison-Wesley. ISBN 0-201-02988-X.

[Aho.Hopcroft.Ullman.1974-5] Alfred V. Aho and John E. Hopcroft and Jeffrey D. Ullman (1974). The Design and Analysis of Computer Algorithms. Reading/MA: Addison-Wesley. ISBN 0-201-00029-6.

[Sipser.1997-6] Michael Sipser (1997). Introduction to the Theory of Computation. Boston/MA: PWS Publishing Co. ISBN 0-534-94728-X.

[Hopcroft.Motwani.Ullman.2003-7] John E. Hopcroft and Rajeev Motwani and Jeffrey D. Ullman (2003). Introduction to Automata Theory, Languages, and Computation (PDF). Upper Saddle River/NJ: Addison Wesley. ISBN 0-201-44124-1.

[8] FOLDOC 무료 온라인 컴퓨팅 사전 유한 상태 기계

[9] ttp://cseweb.ucsd.edu/~ccalabro/fsa.pdf^{[베어 URL PDF]}

[10] Alan, C., Avgustinov, P., Christensen, A. S., Hendren, L., Kuzins, S., Lotak, O., de Moor, O., Sereni, D., Sittampalam, G. 및 Tible, 2005.Wayback Machine에서 AspectJ Archived 2009-09-18에 자유 변수를 사용한 트레이스 매칭을 추가합니다.오브젝트 지향 프로그래밍, 시스템, 언어 및 애플리케이션에 관한 제20회 ACM SIGPLAN 회의의 속행(2005년 10월 16일~20일)OPSLA '05년ACM, 뉴욕, 뉴욕, 345-364

[11] 이력: 최신 프레젠테이션에 대해서는 [1]을 참조해 주세요.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

v t 줄들
문자열 메트릭	대략적인 문자열 매칭 비트맵 알고리즘 다메라우-레벤슈테인 거리 거리 편집 게스탈트 패턴 매칭 해밍 거리 자로-윙클러 거리 리 거리 레벤슈테인 오토마톤 레벤슈테인 거리 바그너-피셔 알고리즘
문자열 검색 알고리즘	사도-장칼로 알고리즘 Boyer-Moore 문자열 검색 알고리즘 보이어-무어-호스풀 알고리즘 크누스-모리스-프랫 알고리즘 라빈-카르프 알고리즘
다중 문자열 검색	아호코라식 Commentz-Walter 알고리즘
정규 표현	정규 표현 엔진 비교 정규 문법 톰슨 구조 비결정론적 유한 오토마톤
시퀀스 얼라인먼트	히르슈베르크 알고리즘 니들맨분쉬 알고리즘 스미스-워터맨 알고리즘
data 구조	DAFSA 서픽스 배열 서픽스 오토마톤 접미사 트리 일반 접미사 트리 출렁 삼원 검색 트리 트리
다른.	해석 패턴 매칭 압축 패턴 매칭 최장 공통 서브시퀀스 최장 공통 서브스트링 순차적 패턴 마이닝 정렬

Search

비결정론적 유한 오토마톤

네임스페이스

더

목차

비공식 소개

형식적 정의

오토마톤

인식된 언어

초기 상태

예

DFA와의 동등성

µ-moves가 있는 NFA

형식적 정의

상태 또는 상태 집합의 폐쇄

확장 전환 기능

예

NFA와의 동등성

닫힘 속성

특성.

실행

NFA 적용

「」를 참조해 주세요.

메모들

레퍼런스

Search

비결정론적 유한 오토마톤

비공식 소개

형식적 정의

오토마톤

인식된 언어

초기 상태

예

DFA와의 동등성

µ-moves가 있는 NFA

형식적 정의

상태 또는 상태 집합의 폐쇄

확장 전환 기능

예

NFA와의 동등성

닫힘 속성

특성.

실행

NFA 적용

「 」를 참조해 주세요.

메모들

레퍼런스

「」를 참조해 주세요.