파워셋 건설

Powerset construction

연산 및 오토마타 이론에서 파워셋 구성이나 서브셋 구성은 비결정론적 유한자동화(NFA)를 동일한 공식 언어를 인식하는 결정론적 유한자동화(DFA)로 변환하기 위한 표준 방법이다.그것은 NFA가 그들의 추가적인 유연성에도 불구하고, 일부 DFA에 의해 인식될 수 없는 어떤 언어도 인식할 수 없다는 것을 확립하기 때문에 이론적으로 중요하다.구성하기 쉬운 NFA를 보다 효율적으로 실행 가능한 DFA로 전환하는 것도 실무에서 중요하다.그러나, NFA가 n개 주를 갖는 경우, 결과 DFA는 최대n 2개 주를 가질 수 있는데, 이는 기하급수적으로 더 큰 숫자로, 때로는 대형 NFA에 대한 건설을 비실용적으로 만든다.

때때로 다른 형태의 오토마타에 대한 유사한 구조와 구별하기 위해 라빈-스코트 파워셋 건설(또는 부분집합 건설)이라고 불리기도 하는 이 공사는 1959년 마이클 O. 라빈과 다나 스콧에 의해 처음 출판되었다.[1]

직감

주어진 입력 문자열에서 DFA의 작동을 시뮬레이션하려면 입력의 접두사를 보고 자동이 도달하는 상태라는 단일 상태를 언제든지 추적해야 한다.대조적으로, NFA를 시뮬레이션하기 위해서는 일련의 상태를 추적할 필요가 있다. 즉, 자동화가 입력의 동일한 접두사를 본 후에 도달하는 모든 상태는 자동화에 의해 이루어진 비결정론적 선택에 따라 결정된다.입력의 특정 접두사 뒤에 S에 도달할 수 있다면, 다음 입력 기호 x 다음에 도달할 수 있는 상태 집합은 S와 x의 결정론적 함수다.따라서 도달 가능한 NFA 상태 집합은 단일 DFA 상태가 DFA 시뮬레이션에서 작동하는 것과 동일한 역할을 하며, 실제로 이 시뮬레이션에 나타나는 NFA 상태 집합은 DFA 상태로 다시 해석될 수 있다.[2]

건설

파워셋 구조는 입력 기호(일명: "moves-moves")를 사용하지 않고 상태 변환을 허용하지 않는 NFA에 가장 직접적으로 적용된다.그러한 자동화는 5투플(Q, σ, T, q0, F)으로 정의될 수 있는데, 여기서 Q는 입력 기호의 집합, T는 전환 함수(상태와 입력 기호를 상태 집합에 매핑), q는0 초기 상태, F는 수용 상태의 집합이다.해당 DFA에는 Q의 하위 집합에 해당하는 상태가 있다.DFA의 초기 상태는 초기 상태의 (1-element) 세트인0 {q}이다.DFA의 전환 기능은 상태 S(Q의 서브셋을 나타냄)와 입력 기호 x를 설정된 T(S,x) = ={T(q,x) q q S에 매핑하는데, 이는 S의 상태에서 x 전환에 도달할 수 있는 모든 상태의 집합이다.DFA의 상태 S는 적어도 S의 멤버가 NFA의 수락 상태일 경우에만 수락 상태.[2][3]

파워셋 구성의 가장 간단한 버전에서, DFA의 모든 상태 집합은 Q의 모든 가능한 하위 집합의 집합인 Q의 파워셋이다.그러나 결과 DFA의 많은 주는 초기 상태로부터 연락이 불가능할 수 있기 때문에 무용지물이 될 수 있다.그 건설의 대체 버전은 실제로 도달할 수 있는 주만 만든다.[4]

ε-모브가 있는 NFA

ε-moves(또는 ε-NFA라고도 함)가 있는 NFA의 경우, ε-moves만 사용하여 특정 주에서 도달할 수 있는 모든 상태 집합인 ε-closure를 계산하여 이를 처리하도록 구조를 수정해야 한다.Van Noord는 파워셋 구조에 이 폐쇄 연산을 통합하는 세 가지 가능한 방법을 알고 있다.[5]

  1. autom-모브 없이 동등한 NFA를 생성하는 전처리 단계로 전체 오토매틱의 closure-폐쇄를 계산한 후, 정기적인 파워셋 구조를 적용하십시오.또한 홉크로프트와 울먼이 논의한 이 버전은 구현이 간단하지만 자연어 처리 애플리케이션에서 흔히 발생하는 것처럼 ε-모브가 많은 오토마타에는 비실용적이다.[6][5]
  2. powerset 연산 중에 알고리즘에서 고려하는 각 상태의\to 을(를) 계산하고 결과를 캐시한다.
  3. During the powerset computation, compute the ε-closure of each subset of states Q' that is considered by the algorithm, and add its elements to Q'.

다중 초기 상태

복수의 초기 상태를 허용하도록 NFA를 정의한 경우,[7] 해당 DFA의 초기 상태는 NFA의 모든 초기 상태의 집합이거나, (NFA가 ε-moves를 가진 경우) ε-moves에 의해 초기 상태에서 도달할 수 있는 모든 상태의 집합이다.

예

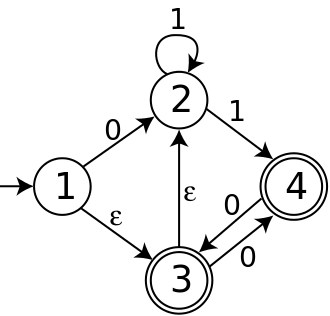
아래의 NFA는 4개의 주를 가지고 있다; 주 1은 초기 상태고 주 3과 주 4는 받아들이고 있다.그것의 알파벳은 두 개의 기호 0과 1로 구성되어 있으며, ε-모브(moves)를 가지고 있다.

NFA-powerset-construction-example.svg

이 NFA에서 생성된 DFA의 초기 상태는 상태 1에서 상태 2로 도달할 수 있는 모든 NFA 상태의 집합이다. 즉, 그것은 설정값 {1,2,3}이다. 입력 기호 0에 의한 {1,2,3}에서 상태 1에서 상태 2로의 화살표 또는 상태 3에서 상태 4로의 화살표에 따라야 한다.또한 주 2와 주 4는 모두 외향적인 mo-모브를 가지고 있지 않다.따라서 T({1,2,3,0) = {2,4}, 같은 추론에 의해 NFA에서 생성된 전체 DFA는 아래와 같다.

DFA-powerset-construction-example.svg

이 예에서 볼 수 있듯이, DFA 시작 상태에서 도달할 수 있는 5개의 주가 있다. NFA 상태 집합의 파워셋에서 나머지 11개 세트는 도달할 수 없다.

복잡성

주요 기사:주의 복잡성
DFA(오른쪽)가 16개 주를 필요로 하는 5개 주(왼쪽)의 NFA.[4]

DFA 주는 NFA 주의 집합으로 구성되기 때문에, n-state NFA는 최대 2개의n 주를 가진 DFA로 변환될 수 있다.[2]모든 n에 대해, 초기 하위 집합에서 모든 상태 하위 집합에 도달할 수 있도록 n-상태 NFA가 존재하므로 변환된 DFA는 정확히 2개의n 상태를 가지며, θ(2n) 최악의 경우 시간 복잡성을 제공한다.[8][9]거의 이 많은 상태를 요구하는 간단한 예로는 문자 {0,1}을(를) 넘는 문자열의 언어가 있으며, 이 언어의 끝에서 n번째는 1이다.그것은 (n + 1)-상태 NFA로 나타낼 수 있지만, 입력의n n 문자 접미사 각각에 하나씩, n=4에 대한 cf. 그림 2개가 필요하다.[4]

적용들

Brzozowski의 DFA 최소화를 위한 알고리즘은 파워셋 구조를 두 번 사용한다.입력 DFA를 역언어용 NFA로 변환하는데, 모든 화살을 뒤집고 초기 및 수용 상태의 역할을 교환하며, 파워셋 구조를 이용하여 NFA를 다시 DFA로 변환한 후 그 과정을 반복한다.그것의 최악의 경우 복잡성은 알려진 다른 DFA 최소화 알고리즘과는 달리 지수적이지만,[10] 많은 예에서 그것은 그것의 최악의 경우 복잡성이 시사하는 것보다 더 빨리 수행된다.

n개 주가 있는 비결정론적 Büchi 자동화를 결정론적 Muller 자동 또는 2개O(n log n) 주가 있는 결정론적 Rabin 자동화로 변환하는 Safra의 건설은 파워셋 건설을 기계의 일부로 사용한다.[11]

참조

  1. ^ Rabin, M. O.; Scott, D. (1959). "Finite automata and their decision problems". IBM Journal of Research and Development. 3 (2): 114–125. doi:10.1147/rd.32.0114. ISSN 0018-8646.
  2. ^ a b c Sipser, Michael (1997). "Theorem 1.19". Introduction to the Theory of Computation. pp. 55–56. ISBN 0-534-94728-X.
  3. ^ Hopcroft, John E.; Ullman, Jeffrey D. (1979). "The equivalence of DFA's and NFA's". Introduction to Automata Theory, Languages, and Computation. Reading Massachusetts: Addison-Wesley. pp. 22–23. ISBN 0-201-02988-X.
  4. ^ a b c Schneider, Klaus (2004). Verification of reactive systems: formal methods and algorithms. Springer. pp. 210–212. ISBN 978-3-540-00296-3.
  5. ^ a b Van Noord, Gertjan (2000). "Treatment of epsilon moves in subset construction". Computational Linguistics. 26 (1): 61–76. arXiv:cmp-lg/9804003. doi:10.1162/089120100561638. S2CID 5622079.
  6. ^ 홉크로프트 & 울만(1979), 페이지 26–27.
  7. ^ Rothe, Jörg (2006). Complexity Theory and Cryptology: An Introduction to Cryptocomplexity. Texts in Theoretical Computer Science. Springer. pp. 21–22. ISBN 9783540285205..
  8. ^ Lupanov, Oleg B. (1963). "A comparison of two types of finite sources". Problemy Kibernetiki. 9: 321–326.
  9. ^ Moore, Frank R. (1971). "On the bounds for state-set size in the proofs of equivalence between deterministic, nondeterministic, and two-way finite automata". IEEE Transactions on Computers. C-20 (10): 1211–1214. doi:10.1109/T-C.1971.223108. S2CID 206618275..
  10. ^ Brzozowski, J. A. (1963). "Canonical regular expressions and minimal state graphs for definite events". Proc. Sympos. Math. Theory of Automata (New York, 1962). Polytechnic Press of Polytechnic Inst. of Brooklyn, Brooklyn, N.Y. pp. 529–561. MR 0175719.
  11. ^ Safra, S. (1988). "On the complexity of ω-automata". Proceedings of the 29th Annual Symposium on Foundations of Computer Science (FOCS '88). Washington, DC, USA: IEEE Computer Society. pp. 319–327. doi:10.1109/SFCS.1988.21948..

추가 읽기