다각도 광산란

멀티앵글광산란(MALS)은 시료에 의해 산란된 빛을 복수의 각도로 측정하는 기술을 기술한다.그것은 빛이 어떻게 산란되는지를 감지함으로써 절대 몰 질량과 용액 속 분자의 평균 크기를 결정하는 데 사용된다.레이저 소스로부터의 시준된 빔이 가장 자주 사용되며, 이 경우 이 기술을 멀티앵글 레이저 광산란(MALL)이라고 할 수 있습니다.레이저라는 단어를 삽입한 것은 기존의 광원(예: Hg-arc 램프)을 사용하여 저각도 측정을 수행할 ^{[citation needed]}수 있다는 것을 확인하려는 의도였다.레이저 및 좁은 폭의 관련 미세 빔이 등장하기 전까지는 이러한 측정에 사용되는 기존 광빔의 폭은 더 작은 산란 각도에서 데이터를 수집하지 못했습니다.최근 몇 년 동안 모든 상용 광산란 계측기가 레이저 광원을 사용하기 때문에 광원에 대한 언급이 필요 없어졌고 MOLS라는 용어가 사용되었습니다.

"다각" 용어는 예를 들어 단일 검출기가 선택한 특정 각도를 포함하는 범위로 이동하거나 특정 각도 위치에 고정된 검출기 배열에 의해 측정된 서로 다른 이산 각도에서 산란 빛을 검출하는 것을 말한다.이와 관련된 몇 가지 응용 프로그램, 데이터 분석 방법 및 그래픽 표현을 포함하여 이 정적 빛 산란과 관련된 물리적 현상에 대한 논의가 제시된다.

배경

조명 샘플의 산란광 측정은 이른바 고전광 산란 측정의 기초를 형성한다.지금까지 이러한 측정은 조명 표본에 대해 원호 모양으로 회전하는 단일^[1]^[2] 검출기를 사용하여 수행되었다.최초의 상용 기구(공식적으로 "산란 광도계"라고 불림)는 1950년대 중반에 도입된 브리스-피닉스 광산란 광도계였고 1960년대 후반에 도입된 소피카 광도계였다.

측정은 일반적으로 산란 강도 또는 산란 방사 강도로 표현되었다.검출기가 아크의 서로 다른 위치에 배치되어 서로 다른 산란 각도에 해당하는 각 위치에 별도의 검출기를 배치하는 개념은 잘 이해되었지만^[3] 1970년대 후반까지 상업적으로 구현되지^[4] 않았다.양자 효율이 다른 복수의 검출기는 다른 응답을 가지므로 이 방식에서 정규화할 필요가 있다.고속 필름의 사용에 기초한 흥미로운 시스템은 1974년 Brunsting과 Mullaney에^[5] 의해 개발되었다.이것은 상대적인 산란 강도를 제공하는 후속 농도계 스캔을 통해 모든 산란 강도 범위를 필름에 기록할 수 있게 했다.특정 각도에서 수집된 강도로 조명된 샘플에 대해 회전하는 단일 검출기를 사용하는 것을 양자역학 용어 미분 단면 ^[7]δ(δ) 이후 미분광 산란이라고^[6] 불렀다.예를 들어 중성자와 같은 원자핵에서 ^[8]산란하여 원자핵의 구조를 연구하기 위해 단면차 측정이 일반적으로 이루어졌다.차동광 산란과 동적광 산란을 구별하는 것이 중요하며, 이 두 가지를 모두 DLS라는 이니셜로 부른다.후자는 상당히 다른 기술을 말하며, 건설적이고 파괴적인 간섭에 의한 산란광의 변동을 측정하는데, 주파수는 열운동, 용액 또는 현탁 중 분자 또는 입자의 브라운 운동과 관련이 있다.

MALS 측정에는 일련의 보조 요소가 필요합니다.그 중에서도 가장 중요한 것은 시준광 또는 집속광선(일반적으로 단색의 시준광선을 생성하는 레이저 광원)으로, 시료의 영역을 비춘다.현대 계측기에서 빔은 일반적으로 측정면에 수직으로 평면 편광되지만, 특히 이방성 입자를 연구할 때 다른 편광을 사용할 수 있습니다.레이저가 도입되기 전에 이전의 측정은 Hg-arc ^{[citation needed]}램프와 같은 광원에서 나오는 편광은 아니지만 초점을 맞춘 광선을 사용하여 수행되었다.또 다른 필수 소자는 측정 대상 시료를 유지하는 광셀이다.또는 유동 시료의 측정을 가능하게 하는 셀 삽입 수단을 사용할 수 있다.단일 입자 산란 특성을 측정해야 할 경우 주변 검출기와 일반적으로 동일한 거리에서 광선을 통해 한 번에 한 입자를 도입할 수 있는 수단이 제공되어야 한다.

비록 대부분의MALS-based 측정은 비행기 탐지기 세트 보통 같은 거리에 이를 통해 조명 빔 패스는 중앙에 위치한 샘플에서를에서 수행되는은 탐지기 구의 표면의 샘플 throu을 통과하는 형태로 누어서, 3차원 versions[9][10]또한 개발되었다.그 gh구체의 직경을 따라 통과하는 입사 광선의 경로와 교차하는 중심.전자의^[9] 틀은 에어로졸 입자를 측정하는 데 사용되었고 후자는^[10] 식물성 플랑크톤과 같은 해양 유기체를 조사하는 데 사용되었다.

기존의 미분광 산란 측정은 현재 사용되는 MLS 기법과 사실상 동일했다.MLS 기법은 일반적으로 이산 검출기 세트의 출력으로부터 다중화된 데이터를 순차적으로 수집하지만, 이전의 차등 광산란 측정 역시 단일 검출기가 한 수집 각도에서 다음 수집 각도로 이동함에 따라 순차적으로 데이터를 수집했다.물론 MLS 구현이 훨씬 빠르지만 동일한 유형의 데이터가 수집되고 동일한 방식으로 해석됩니다.따라서 두 용어는 동일한 개념을 나타냅니다.차등광산란 측정의 경우 광산란광도계는 1개의 검출기를 가지며, MLS광도계는 일반적으로 복수의 검출기를 가진다.

또 다른 유형의 MLS 장치는 1971년 Litton Systems Inc.^[12]를 위해 George 등이 발명한 광 패턴 검출기를 기반으로 1974년 Salzmann ^[11]등에 의해 개발되었다.Litton 검출기는 구면 렌즈의 후면 초점면의 빛 에너지 분포를 샘플링하여 기하학적 관계를 샘플링하고 필름 투명도에 기록된 물체의 스펙트럼 밀도 분포를 샘플링하기 위해 개발되었다.

Salzman 등에 의한 Litton 검출기의 적용은 0°와 30° 사이의 32개의 작은 산란 각도에서 측정했으며, 가장 중요한 각도가 정적 빛 산란을 위한 전방 각도이기 때문에 광범위한 방위각에서 평균을 산출했다.1980년까지, Bartholi et al.^[13]는 2.1° 분해능으로 2.5° ≤ θ 177 177.5° 범위에 걸쳐 30개의 극각에서 측정이 가능하도록 타원 반사경을 사용하여 이산 산란 각도에서 산란을 측정하는 새로운 접근방식을 개발했다.

멀티앵글 시스템의 상용화는 1977년 Science Spectrum,^[14] Inc.가 USFDA용으로 개발된 맞춤형 바이오아세이 시스템을 위한 플로우 스루 모세관 시스템을 특허 취득하면서 시작되었다.8개의 이산 검출기가 포함된 최초의 상용 MLS 계측기가 S.C.에 납품되었다.1983년 ^[15]와이어트 테크놀로지 컴퍼니의 존슨 앤 손(Johnson and Son)이 1984년에 최초의 15대의 검출기 흐름 계측기(Dawn-F)^[16]를 AMOCO에 매각했다.1988년에는 단일 에어로졸 입자의 산란 특성을 측정하기 위해 3차원 구성이 도입되었습니다^[9].이와 동시에 수중 장치는 단일 식물성 플랑크톤의 ^[10]산란된 빛 특성을 측정하기 위해 만들어졌다.신호는 광섬유로 수집되어 개별 광전자 증배관에 전송되었다.2001년 12월경에는 CCD 검출기를 이용하여 7개의 산란각을 측정하는 기기가 상용화되었다(BI-MwA: Brookhaven Instruments Corporation, Hotlsville, NY).

MALS 광도계에 의한 측정과 관련된 문헌은 ^[17]^[18]광범위하다. 입자/분자의 배치 측정과 크기 제외^[19] 크로마토그래피(SEC), 역상 크로마토그래피^[20](RPC), 필드 흐름 분획^[21](FFF)과 같은 크로마토그래피 수단에 의한 분획에 따른 측정과 관련된다.

이론.

다각형 위치에서 이루어지는 산란 측정의 해석은 측정된 입자 또는 분자의 선험적 특성에 대한 약간의 지식에 의존합니다.그러한 산란체의 다른 등급의 산란 특성은 적절한 이론을 적용함으로써 가장 잘 해석될 수 있다.예를 들어, 다음과 같은 이론이 가장 자주 적용된다.

레일리 산란은 가장 단순하며 입사 파장보다 훨씬 작은 물체에 의한 빛이나 다른 전자기 복사의 탄성 산란을 나타냅니다.이런 종류의 산란은 낮 동안 하늘의 푸른색을 담당하며 파장의 4승에 반비례한다.

이라는 가정이 흩어지는 알갱이가 굴절률, n1은 바로 주변 매체의 굴절률, n0에 가지고 해병대 항공 군수 대대 측정 해석하는데 그 Rayleigh–Gans 근사치인 수단이다.만약 있고 m-1<>를 취하다 m)n1/n0.<1매우 작은 요소, 각각의로 구성되었고 그러한 입자로 간주될 것이다.레일리 산란 입자로 표현될 수 있습니다.따라서 더 큰 입자의 각 작은 원소는 다른 원소와 독립적으로 산란한다고 가정한다.

로렌츠-미에^[22] 이론은 균일한 구면 입자에 의한 빛의 산란을 해석하는데 사용된다.레일리-간즈 근사치와 로렌츠-미에 이론은 1 - m → 0인 한계 내의 균질 구에 대해 동일한 결과를 산출한다.

로렌츠-미에 이론은 기준 ^[23]당 구형 대칭 입자로 일반화될 수 있다.보다 일반적인 형태와 구조는 에르마에 ^[24]의해 다루어져 왔다.

산란 데이터는 일반적으로 용액의 Rayleigh 비율 또는 운반체 유체의 Rayleigh 비율 및 기타 백그라운드 기여(있는 경우)를 뺀 단일 입자 이벤트의 Rayleigh 비율로 정의되는 이른바 초과 Rayleigh 비율로 표현됩니다.각도 θ에 놓여 있고 고체 각도 δ를 서브텐딩하는 검출기에서 측정된 Rayleigh Ratio는 단위 입사 강도 당₀ 단위 고체 각도 당 빛의 강도 I, 단위 조명 산란 부피 δV로 정의된다.산란된 빛이 검출기에 도달하는 산란 부피 δV는 일반적으로 개구부, 렌즈 및 정지부에 의해 제한된 검출기의 시야에 의해 결정된다.이제 레이저에 의해 생성된 미세한 광선에 의해 조명되는 ml당 동일한 입자/분자 N개의 현탁액에서 평면으로 이루어지는 MLS 측정을 생각해 보겠습니다.빛이 검출기 평면에 수직으로 편광된다고 가정합니다.현탁액에 의해 산란되는 광도를 초과하는 각도 θ에서 검출기에 의해 측정된 산란광 강도는 다음과 같다.

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

(

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

)

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

N

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

V (

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

r )

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

i (

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

) \

display

style I ( \ theta ) =

flac

{

I

_ {

0 } N

\

Delta

V } { (

kr

)^

2}i

( \

theta

)

I(\theta )={\frac {I_{0}N\Delta V}{(kr)^{2}}}i(\theta )

,

여기서 i(입자)는 단일 입자의 산란^[1] 함수, k = 2µn₀/latrix₀, n은₀ 현탁액의 굴절률, θ는₀ 입사광의 진공 파장이다.초과 레일리 비율 R(θ)은 다음과 같이 구한다.

R(\theta )={\frac {I(\theta )r^{2}}{I_{0}\Delta V}}=Ni(\theta )/k^{2}

I_{0}\Delta

V

}}=Ni(\theta)/k^{2

굴절률 n이 현탁유체의 굴절률₀ n과 매우 유사한 반지름 a의 단순한 균질구체라도, 즉 레일리-간스 근사치에서는 산란함수는 비교적 복잡한 양이다.

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

(

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

-

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

2 (

2

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

sin

fr

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

)

i(\theta )={\frac {k^{2}V^{2}\left|{m-1}\right|^{2}}{4\pi ^{2}}}G^{2}\left({2ka\sin {\frac {\theta }{2}}}\right)

{

k

^ {

2

}

V

^ {

2

} \

left ^

{ m - 1

}

{

4

\

pi

^

2

}

G

^

2 （ fr

2

）

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

k={\frac {2\pi n_{0}}{\lambda _{0}}}

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

(

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

)

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

2 ( sin

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

- -

G(\xi )={\frac {3}{\xi ^{2}}}(\sin \xi -\xi \cos \xi )

cos

display

) {

display

G ( \

xi

) =

sn \ xi \ cos

\

xi

{ \

xi

} 、

k={\frac {2\pi n_{0}}{\lambda _{0}}}

= 2

k={\frac {2\pi n_{0}}{\lambda _{0}}}

0

k={\frac {2\pi n_{0}}{\lambda _{0}}}

0

= display style kfrac 2

\ 0 \ 0 \ 0 λ 0 λ 0 \ 0 λ 0 {\ 0 {\ 0 {\ 0 {\ 0 λ 0 λ 0 { 0 { 0 { 0 { 0 { 0 { 0 g 0 g 0 { 0 g 0

θ는₀ 진공상태에서 입사광의 파장입니다.

적용들

Zim 그림 및 배치 수집

짐 플롯

MALS는 용액에 있는 분자의 질량과 크기를 특징짓는 데 가장 일반적으로 사용됩니다.브루노 짐(Bruno H. Zimm)이 그의 논문 "빛 산란의 각도 변동 측정 및 해석 방법; 폴리스티렌 ^[1]용액에 대한 예비 결과"에서 논의한 것과 같은 MALS의 초기 구현에는 투명한 용기 내에 포함된 샘플에 대해 회전하는 단일 검출기를 사용하는 것이 포함되었다.이와 같은 비유동 검체의 MALS 측정은 일반적으로 "배치 측정"이라고 합니다.여러 알려진 낮은 농도에서와 다양한 각도에서 샘플에 흩어져 있던 탐지 샘플을 만듦으로써,:K∗ cRθ{\displaystyle{\frac{K^{*}c}{R_{\theta}}}}과 죄 2⁡ θ 2+어디 c는 conce kc{\displaystyle\sin ^{2}{\frac{\theta}{2}}+kc}를 계획함으로썬 Zimm plot[25]를 만들 수 있습니다.ntr시료와 k의 이온은 $\sin ^{2}{\frac {\theta }{2}}$ 와 $\sin ^{2}{\frac {\theta }{2}}$ 2 $\sin ^{2}{\frac {\theta }{2}}$ $\sin ^{2}{\frac {\theta }{2}}$ {\ $displaystyle \sin ^{2}{\frac$ {\ $theta$ }{ $2}}$ 을 $\sin ^{2}{\frac {\theta }{2}}$ (를) 동일한 수치 범위에 넣기 위해 사용되는 스트레치 팩터이다.

플롯을 작성하면 0의 각도와 0의 농도로 추정할 수 있으며, 플롯 분석을 통해 c=0 라인의 초기 기울기에서 샘플 분자의 평균 제곱 반지름과 농도와 각도가 모두 0인 지점에서 분자의 몰 질량을 얻을 수 있다.수집된 모든 데이터를 통합한 Zim 그림(일반적으로 "글로벌 적합"이라고 함)이 현대 배치 ^[26]분석에서 Zim 그림을 대체했습니다.

SEC 및 흐름 모드

폴리스티렌 구체의 MALS 신호

크기 제외 크로마토그래피(SEC)의 등장으로, 교정 기법에 의존하지 않고 온라인 농도 검출기와 함께 MLS 측정이 사용되어 컬럼에서 유출되는 시료 분율의 절대 몰 질량과 크기를 결정하기 시작했다.이러한 흐름 모드의 MLS 측정은 필드 흐름 분류, 이온 교환 크로마토그래피 및 역상 크로마토그래피와 같은 다른 분리 기술로 확장되었습니다.

광산란 데이터의 각도 의존성은 SEC에 의해 분리된 폴리스티렌 구체의 혼합 그림으로 아래에 나와 있다.가장 작은 두 검체(오른쪽 가장 빠른 검체)가 마지막으로 용출되어 각도 의존성을 보이지 않습니다.오른쪽 두 번째 샘플은 낮은 산란 각도에서 강도가 증가하는 선형 각도 변동을 보여줍니다.왼쪽의 가장 큰 표본이 먼저 용출하여 비선형 각도 변동을 보여줍니다.

MALS 측정 유틸리티

몰 질량 및 크기

BSA 분리 및 MM 배포

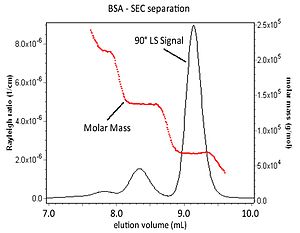
MALS를 SEC 등의 시료분리수단에 따른 인라인 농도검출기와 결합함으로써 용출샘플의 몰질량을 근평균제곱반경에 더해 계산할 수 있다.아래 그림은 BSA Aggregate의 크로마토그래피 분리를 나타내고 있습니다.MLS 검출기의 90° 광산란 신호와 각 용출 슬라이스에 대한 몰 질량 값이 표시됩니다.

분자 상호작용

MALS는 분자의 몰 질량과 크기를 제공할 수 있기 때문에 단백질-단백질 결합, 올리고머화 및 자가조립, 결합 및 해리의 역학에 대한 연구를 가능하게 한다.시료의 몰 질량과 농도를 비교함으로써 상호작용하는 분자의 결합 친화력 및 화학량법을 결정할 수 있다.

분기 및 분자 구조

폴리머의 분기 비율은 무작위로 분기된 폴리머의 분기 단위 수와 스타 분기된 폴리머의 팔 수와 관련이 있으며 Zim과 Stockmayer에 의해 다음과 같이 정의되었습니다.

$({displaystyle g=marchfrac {R_{b}^2}}{R_{l}^2}}})$

$R^{2}$ 서 R 2 $({$ R $^{2}})$ 는 $R^{2}$ 몰 ^[27]질량이 동일한 분기 및 선형 고분자의 평균 제곱 반지름입니다.위와 같이 MALS를 농도검출기와 연계하여 제곱근 평균 반지름 대 몰 질량의 로그 로그도를 작성한다.이 그래프의 기울기는 분기 비율 ^[28]g를 산출합니다.

분기와 더불어 크기 대 몰 질량의 로그 로그 그림은 고분자의 모양 또는 구조를 나타냅니다.플롯의 기울기가 증가하면 구형에서 랜덤 코일, 선형으로 폴리머의 배치가 변화한다.MALS로부터의 평균 제곱 반지름과 DLS 측정으로 얻은 유체 역학적 $r_{h}$ $r_{h}$ h {\ $displaystyle r_{h}}$ 를 $r_{h}$ 조합하면 각 고분자 크기 분율마다 형상 계수 = ${\frac {r_{g}}{r_{h}}}$ g ${\frac {r_{g}}{r_{h}}}$ h {\ $displaystyle {r_{g}}$ { $r_{h$ 가 된다.

기타 응용 프로그램

다른 MLS 응용 프로그램에는 나노 입자 크기 조정,^[29]^[30]^[31] 단백질 응집 연구, 단백질-단백질 상호작용, 전기영동성 또는 제타 전위가 포함됩니다.MALS 기술은 의약품 안정성과 나노의학에서의 사용을 연구하기 위해 채택되었다.

레퍼런스

^ ^a ^b ^c B. A. Zimm (1948). "Apparatus and methods for measurement and interpretation of the angular variation of light scattering; preliminary results on polystyrene solutions". J. Chem. Phys. 16 (12): 1099–1116. Bibcode:1948JChPh..16.1099Z. doi:10.1063/1.1746740.
^ B. A. Brice; M. Halwer & R. Speiser (1950). "Photoelectric light scattering photometer for determining high molecular weights". J. Opt. Soc. Am. 40 (11): 768–778. Bibcode:1950JOSA...40..768B. doi:10.1364/JOSA.40.000768.
^ 미국 특허의 P. J. 와이어트는 1968년 출원했다.
^ G. C. Salzmann; J. M. Crowell; C. A. Goad; K. M. Hansen; et al. (1975). "A Flow-System Multiangle Light-Scattering Instrument for Cell Characterization". Clinical Chemistry. 21 (9): 1297–1304. doi:10.1093/clinchem/21.9.1297. PMID 1149235.
^ A. Brunsting & P. F. Mullaney (1974). "Differential Light Scattering from Spherical Mammalian Cells". Biophys. J. 14 (6): 439–453. Bibcode:1974BpJ....14..439B. doi:10.1016/S0006-3495(74)85925-4. PMC 1334522. PMID 4134589.
^ P. J. Wyatt (1968). "Differential Light Scattering: A Physical Method for Identifying Living Bacterial Cells". Applied Optics. 7 (10): 1879–1896. Bibcode:1968ApOpt...7.1879W. doi:10.1364/AO.7.001879. PMID 20068905.
^ Cf. L. I. 쉬프, Quantum Mechanics(McGrow-Hill Book Company, 뉴욕 1955).
^ S. Fernbach (1958). "Nuclear Radii as Determined by Scattering of Neutrons". Rev. Mod. Phys. 30 (2): 414–418. Bibcode:1958RvMP...30..414F. doi:10.1103/RevModPhys.30.414.
^ ^a ^b ^c P. J. Wyatt; Y. J. Chang; C. Jackson; R. G. Parker; et al. (1988). "Aerosol Particle Analyzer". Applied Optics. 27 (2): 217–221. Bibcode:1988ApOpt..27..217W. doi:10.1364/AO.27.000217. PMID 20523583.
^ ^a ^b ^c P. J. Wyatt & C. Jackson (1989). "Discrimination of Phytoplankton via Light-Scattering Properties". Limnology & Oceanography. 34 (I): 96–112. Bibcode:1989LimOc..34...96W. doi:10.4319/lo.1989.34.1.0096.
^ G. C. Salzmann; J. M. Crowell; C. A. Goad; K. M. Hansen; et al. (1975). "A Flow-System Multiangle Light-Scattering Instrument for Cell Characterization". Clinical Chemistry. 21 (9): 1297–1304. doi:10.1093/clinchem/21.9.1297. PMID 1149235.>
^ N. 조지, A. 스핀들, J. T.미국 특허 3689772A(1972)의 Thomasson은 1971년 출원했다.
^ M. Bartholdi; G. C. Salzman; R. D. Hiebert & M. Kerker (1980). "Differential light scattering photometer for rapid analysis of single particles in flow". Applied Optics. 19 (10): 1573–1581. Bibcode:1980ApOpt..19.1573B. doi:10.1364/AO.19.001573. PMID 20221079.
^ L. V. 말다렐리, D.T. Phillips, W. L. Proctor, P. J. Wiret 및 T. C. Urquhart, Programmable Action Sampler System, 미국 특허 4,140,018(1979)은 1977년 출원했다.
^ "Evolution of Wyatt Technology Corp". www.americanlaboratory.com. Retrieved 2017-02-23.
^ "museum about". www.wyatt.com. Retrieved 2017-02-23.
^ 예를 들어 화학적 추상화를 참조하십시오.
^ "MALS Bibliography". www.wyatt.com. Retrieved 2017-02-23.
^ A. M. Striegel; W. W. Yau; J. J. Kirkland & D. D. Bly (2009). Modern Size-Exclusion Liquid Chromatography: Practice of Gel Permeation and Gel Filtration Chromatography. John Wiley and Sons. ISBN 978-0-471-20172-4.
^ I. V. Astafieva; G. A. Eberlein; Y. J. Wang (1996). "Absolute on-line molecular mass analysis of basic fibroblast growth factor and its multimers by reversed-phase liquid chromatography with multi-angle laser light scattering detection". Journal of Chromatography A. 740 (2): 215–229. doi:10.1016/0021-9673(96)00134-3. PMID 8765649.
^ M. Schimpf; K. Caldwell; J. C. Giddings, eds. (2000). Field-Flow Fractionation Handbook. Wiley-IEEE. ISBN 978-0-471-18430-0.
^ L. V. Lorenz (1890). "Light propagation in and outside a sphere illuminated by plane waves of light". Videnski.Selsk.Skrifter. 6: 1–62.
^ P. J. Wyatt (1962). "Scattering of Electromagnetic Plane Waves from Inhomogeneous Spherically Symmetric Objects". Physical Review. 127 (5): 1837–1843. Bibcode:1962PhRv..127.1837W. doi:10.1103/PhysRev.127.1837.Balázs, Louis (1964). "Errata Ibid". Physical Review. 134 (7AB): AB1. Bibcode:1964PhRv..134....1B. doi:10.1103/physrev.134.ab1.2.
^ V.A. Erma (1968a). "An exact solution for the scattering of electromagnetic waves from conductors of arbitrary shape: I. Case of cylindrical symmetry". Physical Review. 173 (5): 1243–1257. Bibcode:1968PhRv..173.1243E. doi:10.1103/physrev.173.1243.V.A. Erma (1968b). "Exact solution for the scattering of electromagnetic waves from conductors of arbitrary shape: II. General case". Physical Review. 176 (5): 1544–1553. Bibcode:1968PhRv..176.1544E. doi:10.1103/physrev.176.1544.V.A. Erma (1969). "Exact solution for the scattering of electromagnetic waves from bodies of arbitrary shape: III. Obstacles with arbitrary electromagnetic properties". Physical Review. 179 (5): 1238–1246. Bibcode:1969PhRv..179.1238E. doi:10.1103/physrev.179.1238.
^ Wyatt, P.J. (1993). "Light Scattering and the Absolute Characterization of Macromolecules". Analytica Chimica Acta. 272: 1–40. doi:10.1016/0003-2670(93)80373-S.
^ Trainoff, S.P. (November 18, 2003). "U.S. Patent No. 6,651,009 B1". US Patent Office.
^ Zimm, Bruno H. (1949). "The Dimensions of Chain Molecules Containing Branches and Rings". J. Chem. Phys. 17 (12): 1301. Bibcode:1949JChPh..17.1301Z. doi:10.1063/1.1747157.
^ Podzimek, Stepan (1994). "The Use of GPC Coupled with a Multiangle Laser Light Scattering Photometer for the Characterization of Polymers. On the Determination of Molecular Weight, Size and Branching". Journal of Applied Polymer Science. 54: 91–103. doi:10.1002/app.1994.070540110.
^ Waghwani HK, Douglas, T (March 2021). "Cytochrome C with peroxidase-like activity encapsulated inside the small DPS protein nanocage". Journal of Materials Chemistry B. 9: 3168–3179. doi:10.1039/d1tb00234a. PMID 33885621.
^ Waghwani HK, Uchida M, Douglas, T (April 2020). "Virus-Like Particles (VLPs) as a Platform for HierarchicalCompartmentalization". Biomacromolecules. 21 (6): 2060–2072. doi:10.1021/acs.biomac.0c00030. PMID 32319761.
^ Wang Y, Uchida M, Waghwani HK, Douglas, T (December 2020). "Synthetic Virus-like Particles for Glutathione Biosynthesis". ACS SyntheticBiology. 9 (12): 3298–3310. doi:10.1021/acssynbio.0c00368. PMID 33232156.

[Zimm1-1] B. A. Zimm (1948). "Apparatus and methods for measurement and interpretation of the angular variation of light scattering; preliminary results on polystyrene solutions". J. Chem. Phys. 16 (12): 1099–1116. Bibcode:1948JChPh..16.1099Z. doi:10.1063/1.1746740.

[2] B. A. Brice; M. Halwer & R. Speiser (1950). "Photoelectric light scattering photometer for determining high molecular weights". J. Opt. Soc. Am. 40 (11): 768–778. Bibcode:1950JOSA...40..768B. doi:10.1364/JOSA.40.000768.

[3] 미국 특허의 P. J. 와이어트는 1968년 출원했다.

[CC21-4] G. C. Salzmann; J. M. Crowell; C. A. Goad; K. M. Hansen; et al. (1975). "A Flow-System Multiangle Light-Scattering Instrument for Cell Characterization". Clinical Chemistry. 21 (9): 1297–1304. doi:10.1093/clinchem/21.9.1297. PMID 1149235.

[5] A. Brunsting & P. F. Mullaney (1974). "Differential Light Scattering from Spherical Mammalian Cells". Biophys. J. 14 (6): 439–453. Bibcode:1974BpJ....14..439B. doi:10.1016/S0006-3495(74)85925-4. PMC 1334522. PMID 4134589.

[Wyatt5-6] P. J. Wyatt (1968). "Differential Light Scattering: A Physical Method for Identifying Living Bacterial Cells". Applied Optics. 7 (10): 1879–1896. Bibcode:1968ApOpt...7.1879W. doi:10.1364/AO.7.001879. PMID 20068905.

[7] Cf. L. I. 쉬프, Quantum Mechanics(McGrow-Hill Book Company, 뉴욕 1955).

[8] S. Fernbach (1958). "Nuclear Radii as Determined by Scattering of Neutrons". Rev. Mod. Phys. 30 (2): 414–418. Bibcode:1958RvMP...30..414F. doi:10.1103/RevModPhys.30.414.

[Wyatt1-9] P. J. Wyatt; Y. J. Chang; C. Jackson; R. G. Parker; et al. (1988). "Aerosol Particle Analyzer". Applied Optics. 27 (2): 217–221. Bibcode:1988ApOpt..27..217W. doi:10.1364/AO.27.000217. PMID 20523583.

[Wyatt2-10] P. J. Wyatt & C. Jackson (1989). "Discrimination of Phytoplankton via Light-Scattering Properties". Limnology & Oceanography. 34 (I): 96–112. Bibcode:1989LimOc..34...96W. doi:10.4319/lo.1989.34.1.0096.

[11] G. C. Salzmann; J. M. Crowell; C. A. Goad; K. M. Hansen; et al. (1975). "A Flow-System Multiangle Light-Scattering Instrument for Cell Characterization". Clinical Chemistry. 21 (9): 1297–1304. doi:10.1093/clinchem/21.9.1297. PMID 1149235.>

[12] N. 조지, A. 스핀들, J. T.미국 특허 3689772A(1972)의 Thomasson은 1971년 출원했다.

[13] M. Bartholdi; G. C. Salzman; R. D. Hiebert & M. Kerker (1980). "Differential light scattering photometer for rapid analysis of single particles in flow". Applied Optics. 19 (10): 1573–1581. Bibcode:1980ApOpt..19.1573B. doi:10.1364/AO.19.001573. PMID 20221079.

[14] L. V. 말다렐리, D.T. Phillips, W. L. Proctor, P. J. Wiret 및 T. C. Urquhart, Programmable Action Sampler System, 미국 특허 4,140,018(1979)은 1977년 출원했다.

[15] "Evolution of Wyatt Technology Corp". www.americanlaboratory.com. Retrieved 2017-02-23.

[16] "museum about". www.wyatt.com. Retrieved 2017-02-23.

[17] 예를 들어 화학적 추상화를 참조하십시오.

[18] "MALS Bibliography". www.wyatt.com. Retrieved 2017-02-23.

[19] A. M. Striegel; W. W. Yau; J. J. Kirkland & D. D. Bly (2009). Modern Size-Exclusion Liquid Chromatography: Practice of Gel Permeation and Gel Filtration Chromatography. John Wiley and Sons. ISBN 978-0-471-20172-4.

[20] I. V. Astafieva; G. A. Eberlein; Y. J. Wang (1996). "Absolute on-line molecular mass analysis of basic fibroblast growth factor and its multimers by reversed-phase liquid chromatography with multi-angle laser light scattering detection". Journal of Chromatography A. 740 (2): 215–229. doi:10.1016/0021-9673(96)00134-3. PMID 8765649.

[21] M. Schimpf; K. Caldwell; J. C. Giddings, eds. (2000). Field-Flow Fractionation Handbook. Wiley-IEEE. ISBN 978-0-471-18430-0.

[22] L. V. Lorenz (1890). "Light propagation in and outside a sphere illuminated by plane waves of light". Videnski.Selsk.Skrifter. 6: 1–62.

[23] P. J. Wyatt (1962). "Scattering of Electromagnetic Plane Waves from Inhomogeneous Spherically Symmetric Objects". Physical Review. 127 (5): 1837–1843. Bibcode:1962PhRv..127.1837W. doi:10.1103/PhysRev.127.1837.Balázs, Louis (1964). "Errata Ibid". Physical Review. 134 (7AB): AB1. Bibcode:1964PhRv..134....1B. doi:10.1103/physrev.134.ab1.2.

[24] V.A. Erma (1968a). "An exact solution for the scattering of electromagnetic waves from conductors of arbitrary shape: I. Case of cylindrical symmetry". Physical Review. 173 (5): 1243–1257. Bibcode:1968PhRv..173.1243E. doi:10.1103/physrev.173.1243.V.A. Erma (1968b). "Exact solution for the scattering of electromagnetic waves from conductors of arbitrary shape: II. General case". Physical Review. 176 (5): 1544–1553. Bibcode:1968PhRv..176.1544E. doi:10.1103/physrev.176.1544.V.A. Erma (1969). "Exact solution for the scattering of electromagnetic waves from bodies of arbitrary shape: III. Obstacles with arbitrary electromagnetic properties". Physical Review. 179 (5): 1238–1246. Bibcode:1969PhRv..179.1238E. doi:10.1103/physrev.179.1238.

[WyattActa-25] Wyatt, P.J. (1993). "Light Scattering and the Absolute Characterization of Macromolecules". Analytica Chimica Acta. 272: 1–40. doi:10.1016/0003-2670(93)80373-S.

[Gobal_Fit_Patent-26] Trainoff, S.P. (November 18, 2003). "U.S. Patent No. 6,651,009 B1". US Patent Office.

[ZimmStockBranch-27] Zimm, Bruno H. (1949). "The Dimensions of Chain Molecules Containing Branches and Rings". J. Chem. Phys. 17 (12): 1301. Bibcode:1949JChPh..17.1301Z. doi:10.1063/1.1747157.

[PodzimekBranching-28] Podzimek, Stepan (1994). "The Use of GPC Coupled with a Multiangle Laser Light Scattering Photometer for the Characterization of Polymers. On the Determination of Molecular Weight, Size and Branching". Journal of Applied Polymer Science. 54: 91–103. doi:10.1002/app.1994.070540110.

[29] Waghwani HK, Douglas, T (March 2021). "Cytochrome C with peroxidase-like activity encapsulated inside the small DPS protein nanocage". Journal of Materials Chemistry B. 9: 3168–3179. doi:10.1039/d1tb00234a. PMID 33885621.

[30] Waghwani HK, Uchida M, Douglas, T (April 2020). "Virus-Like Particles (VLPs) as a Platform for HierarchicalCompartmentalization". Biomacromolecules. 21 (6): 2060–2072. doi:10.1021/acs.biomac.0c00030. PMID 32319761.

[Wang2020-31] Wang Y, Uchida M, Waghwani HK, Douglas, T (December 2020). "Synthetic Virus-like Particles for Glutathione Biosynthesis". ACS SyntheticBiology. 9 (12): 3298–3310. doi:10.1021/acssynbio.0c00368. PMID 33232156.

[1]

[2]

[3]

[4]

[5]

[7]

[6]

[8]

[9]

[10]

[12]

[11]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[26]

[27]

[28]

[29]

[30]

[31]

Search