선도오더 용어

Leading-order term

수학 방정식, 식 또는 모형 내의 선행 항(또는 수정)은 크기가 가장 큰 항이다.[1][2]변수가 변함에 따라 방정식의 여러 항의 크기가 변경되므로 어떤 항이 선행하는지 또한 변경될 수 있다.

와 이해를 복잡한 수학적 모델의 다양한 단순화시키는 유력한 일반적인 방법은 변수와 매개 변수의 특별한 크기에 대한 조건들은 큰(며 따라서 가장 중요한),의 행동과 이 조건(무시할 수 있는으로서 다른 작은 조건에 관한)에 의해 생산된 개별적으로 분석 조사하기 위함이다.[3][4]이것은 주요 행동을 제공한다 – 참된 행동은 이것으로부터 아주 작은 편차일 뿐이다.이러한 주요 행동은 엄밀히 선도적인 용어만으로 충분히 잘 포착될 수도 있고, 약간 더 작은 용어들도 포함되어야 한다고 결정할 수도 있다.이 경우 선행 주문 용어는 이 전체 용어 그룹을 의미하기 위해 비공식적으로 사용될 수 있다.단지 선행 조건 그룹에 의해 생성되는 행동을 모형의 선행 조건 행동이라고 한다.

기본 예

개별 항의 크기3(y = x + 5x + 0.1). (선도 순서는 분홍색으로 강조 표시됨)
x 0.001 0.1 0.5 2 10
x3 0.000000001 0.001 0.125 8 1000
5배 0.005 0.5 2.5 10 50
0.1 0.1 0.1 0.1 0.1 0.1
y 0.105000001 0.601 2.725 18.1 1050.1

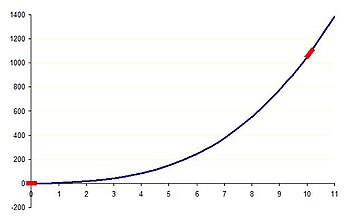
y = x3 + 5x + 0.1 등식을 고려하십시오.x의 다섯 가지 다른 값에 대해 표는 이 방정식의 네 항 크기 및 어떤 항이 선행하는지 보여 준다.x가 더 증가하면 선도주문조건은3 x와 y로 유지되지만, x가 감소했다가 점점 음수가 되면서 다시 선도주문조건이 바뀌는 것이다.

두 항을 거의 동일한 순서 또는 크기로 간주해야 하는 경우 엄격한 컷오프는 없다.한 가지 가능한 경험 법칙은 서로 10배(크기율 1배) 이내의 두 항은 거의 같은 순서로 간주해야 하며, 100배(크기율 2배) 이내의 항은 그렇지 않아야 한다는 것이다.그러나 중간은 회색 영역이기 때문에 용어가 대략 선도적인 것으로 간주되고 그렇지 않은 경우 고정된 경계가 없다.대신에 항은 변수가 변함에 따라 점점 희미해진다.모형의 항이 선도 순서(또는 대략 선도 순서)인지, 그렇지 않을 경우 무시해도 될 정도로 작은지(두 개의 다른 질문)를 결정하는 것은 종종 조사와 판단의 문제로서 맥락에 따라 달라질 것이다.

선도-주문 행동

선행 항이 하나만 있는 방정식은 가능하지만 드물다[dubious – discuss].예를 들어, 방정식 100 = 1 + 1 + 1 + ...+ 1, (우측 면이 1001로 구성된 경우).변수와 모수에 대한 값의 특정 조합의 경우 방정식은 일반적으로 최소 두 개의 선행 항과 다른 저차 항을 포함한다.이 경우 저차 항, 그리고 저차 항과 같은 크기(아마도 제2, 제3의 유의미한 수치)인 선도 항들의 부분은 무시해도 좋다고 가정함으로써 이러한 저차 항과 선도 항들의 일부를 모두 삭제함으로써 새로운 방정식을 형성할 수 있다.나머지 항은 선행 방정식, 즉 선행 순서 균형,[5] 또는 지배적인 균형을 제공하며,[6][7][8] 이러한 항만을 포함하는 새로운 방정식을 만드는 것을 선도 순서에 대한 방정식을 취하는 것으로 알려져 있다.이 새로운 방정식의 해법은 원래 방정식의 선도적 해법이라고[9][10] 불린다.이 새로운 방정식에 의해 주어진 행동을 분석하면 변수와 매개변수의 이러한 값에 대한 모델의 선행 순서 동작을[11][12] 제공한다.이 근사치를 만들 때 오차의 크기는 일반적으로 무시되는 최대 항의 크기입니다.

y = x3 + 5x + 0.1의 그래프.x = 0.001에서 선행 순서 또는 주 동작은 y가 일정하다는 것이고 x = 10에서 y는 x와 함께 입체적으로 증가한다는 것이다.

위 예제의 선도적인 행동을 이해하고 싶다고 가정합시다.

  • x = 0.001일 때, x와3 5x 항은 무시해도 되는 것으로 간주될 수 있으며, 나머지 두 항에서 세 번째 소수 자릿수의 모든 값과 함께 삭제될 수 있다.이것은 선도주문 잔액 y = 0.1을 제공한다.따라서 x=0.001에서 이 방정식의 선행 순서는 y가 일정하다는 것이다.
  • 마찬가지로, x = 10일 때, 5x 및 0.1 항은 무시해도 되는 것으로 간주될 수 있으며, 나머지 두 항에 있는 세 번째 유의미한 그림의 값과 함께 삭제될 수 있다.이것은 선도-주문 잔액 y = x를3 제공한다.따라서 x=10에서 이 방정식의 선행 순서는 y가 x와 함께 입체적으로 증가한다는 것이다.

따라서 y의 주요 행동은 x의 어떤 값에서도 조사될 수 있다.선도주문 행태는 더 많은 용어들이 선도주문일 때 더 복잡하다.x=2에서는 x에 대한 y의 입방체 및 선형 종속성 사이에 선행 순서 균형이 있다.

선도적 균형과 행동을 찾는 이 설명은 프로세스에 대한 개략적인 설명만 제공하므로 수학적으로 엄격하지 않다는 점에 유의하십시오.

차세대주문

물론 y는 실제로 x = 0.001에서 완전히 일정하지는 않다 – 이것은 단지 이 지점 근처에서 그것의 주요 행동일 뿐이다.선행(또는 대략 선행) 항만 유지하고 다른 모든 작은 항을 무시할 수 있는 수준으로 유지하는 것이 불충분할 수 있으므로(예를 들어, 미래 예측을 위해 모형을 사용할 때), 다음으로 큰 항 집합도 유지할 필요가 있을 수 있다.이를 차세대 주문(NLO) 용어 또는 수정이라고 할 수 있다.[13][14]그 이후의 다음 항은 NLO(Next-to-Next-to-Leading Order) 항 또는 수정이라고 할 수 있다.[15]

사용법

일치된 점근 팽창

각 서브 도메인에서 정확한 근사치 솔루션이 선도적 해결책인 경우, 선도적 단순화 기법은 대응된 점증적 팽창 방법과 함께 사용된다.[3][16][17]

Navier 단순화–스토크 방정식

특정 유체 흐름 시나리오의 경우 (매우 일반) Navier–스토크 방정식은 선도적 요소만을 고려하여 상당히 단순화할 수 있다.예를 들어, 스톡스 흐름 방정식.[18]또한 윤활 이론의 박막 방정식.

참고 항목

참조

  1. ^ J.K.헌터, 점근 분석 및 특이 섭동 이론, 2004.http://www.math.ucdavis.edu/~http://www.math.ucdavis.edu//notes/asy.pdf
  2. ^ NYU 과정 노트
  3. ^ a b Mitchell, M. J.; et al. (2010). "A model of carbon dioxide dissolution and mineral carbonation kinetics". Proceedings of the Royal Society A. 466 (2117): 1265–1290. Bibcode:2010RSPSA.466.1265M. doi:10.1098/rspa.2009.0349.
  4. ^ Woollard, H. F.; et al. (2008). "A multi-scale model for solute transport in a wavy-walled channel" (PDF). Journal of Engineering Mathematics. 64 (1): 25–48. Bibcode:2009JEnMa..64...25W. doi:10.1007/s10665-008-9239-x.
  5. ^ Sternberg, P.; Bernoff, A. J. (1998). "Onset of Superconductivity in Decreasing Fields for General Domains". Journal of Mathematical Physics. 39 (3): 1272–1284. Bibcode:1998JMP....39.1272B. doi:10.1063/1.532379.
  6. ^ Salamon, T.R.; et al. (1995). "The role of surface tension in the dominant balance in the die swell singularity". Physics of Fluids. 7 (10): 2328–2344. Bibcode:1995PhFl....7.2328S. doi:10.1063/1.868746. Archived from the original on 2013-07-08.
  7. ^ Gorshkov, A. V.; et al. (2008). "Coherent Quantum Optical Control with Subwavelength Resolution". Physical Review Letters. 100 (9): 93005. arXiv:0706.3879. Bibcode:2008PhRvL.100i3005G. doi:10.1103/PhysRevLett.100.093005. PMID 18352706. S2CID 3789664.
  8. ^ Lindenberg, K.; et al. (1994). "Diffusion-Limited Binary Reactions: The Hierarchy of Nonclassical Regimes for Correlated Initial Conditions" (PDF). Journal of Physical Chemistry. 98 (13): 3389–3397. doi:10.1021/j100064a020.
  9. ^ Żenczykowski, P. (1988). "Kobayashi–Maskawa matrix from the leading-order solution of the n-generation Fritzsch model". Physical Review D. 38 (1): 332–336. Bibcode:1988PhRvD..38..332Z. doi:10.1103/PhysRevD.38.332. PMID 9959017.
  10. ^ Horowitz, G. T.; Tseytlin, A. A. (1994). "Extremal black holes as exact string solutions". Physical Review Letters. 73 (25): 3351–3354. arXiv:hep-th/9408040. Bibcode:1994PhRvL..73.3351H. doi:10.1103/PhysRevLett.73.3351. PMID 10057359. S2CID 43551044.
  11. ^ Hüseyin, A. (1980). "The leading-order behaviour of the two-photon scattering amplitudes in QCD". Nuclear Physics B. 163: 453–460. Bibcode:1980NuPhB.163..453A. doi:10.1016/0550-3213(80)90411-3.
  12. ^ Kruczenski, M.; Oxman, L.E.; Zaldarriaga, M. (1999). "Large squeezing behaviour of cosmological entropy generation". Classical and Quantum Gravity. 11 (9): 2317–2329. arXiv:gr-qc/9403024. Bibcode:1994CQGra..11.2317K. doi:10.1088/0264-9381/11/9/013. S2CID 13979794.
  13. ^ Campbell, J.; Ellis, R.K. (2002). "Next-to-leading order corrections to W + 2 jet and Z + 2 jet production at hadron colliders". Physical Review D. 65 (11): 113007. arXiv:hep-ph/0202176. Bibcode:2002PhRvD..65k3007C. doi:10.1103/PhysRevD.65.113007. S2CID 119355645.
  14. ^ Catani, S.; Seymour, M.H. (1996). "The Dipole Formalism for the Calculation of QCD Jet Cross Sections at Next-to-Leading Order". Physics Letters B. 378 (1): 287–301. arXiv:hep-ph/9602277. Bibcode:1996PhLB..378..287C. doi:10.1016/0370-2693(96)00425-X. S2CID 15422325.
  15. ^ Kidonakis, N.; Vogt, R. (2003). "Next-to-next-to-leading order soft-gluon corrections in top quark hadroproduction". Physical Review D. 68 (11): 114014. arXiv:hep-ph/0308222. Bibcode:2003PhRvD..68k4014K. doi:10.1103/PhysRevD.68.114014. S2CID 5943465.
  16. ^ Rubinstein, B.Y.; Pismen, L.M. (1994). "Vortex motion in the spatially inhomogeneous conservative Ginzburg–Landau model" (PDF). Physica D: Nonlinear Phenomena. 78 (1): 1–10. Bibcode:1994PhyD...78....1R. doi:10.1016/0167-2789(94)00119-7.
  17. ^ Kivshar, Y.S.; et al. (1998). "Dynamics of optical vortex solitons" (PDF). Optics Communications. 152 (1): 198–206. Bibcode:1998OptCo.152..198K. doi:10.1016/S0030-4018(98)00149-7. Archived from the original (PDF) on 2013-04-21. Retrieved 2012-10-31.
  18. ^ 코넬 대학교 노트