켈빈-헬름홀츠 불안정성

Kelvin–
켈빈과 혼동하지 말구요헬름홀츠 메커니즘.
시간 켈빈의 수치 시뮬레이션-헬름홀츠 불안정성

켈빈-헬름홀츠 불안정성(Lord Kelvin and Hermann von Helmholtz 이후)은 단일 연속 유체에서 속도 전단이 발생하거나 두 유체 사이의 계면에서 속도 차이가 발생할 때 발생하는 유체 불안정성입니다. 켈빈-헬름홀츠 불안정성은 지구의 구름층이나 목성의 적점과 같은 행성과 달의 대기, 태양과 다른 별의 대기에서 볼 수 있습니다.[1]

레이놀즈 수가 적은 상태에서 공간적으로 2D 켈빈-헬름홀츠 불안정성을 발전시킵니다. 접선 속도의 입구에 부과된 작은 섭동은 계산 상자에서 진화합니다. 레이놀즈 수가 높으면 작은 규모의 움직임이 증가하는 것으로 표시됩니다.

이론개요 및 수학개념

호주 듀발산 [2]상공에서 구름에 의해 보이는 변동성으로 알려진 KH 불안정
토성 대기의 두 밴드의 상호작용으로 형성된 토성의 KH 불안정성
켈빈-헬름홀츠, 대서양 수심 500m에 물이 넘칩니다.
2차 2차원 유한체적법을 이용한 KH 불안정성의 애니메이션

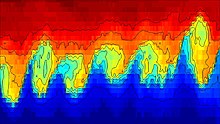
유체 역학은 다른 속도로 움직이는 다른 밀도의 유체 내에서 불안정의 시작과 난류 흐름으로의 전환을 예측합니다.[3] 표면 장력이 무시되면 속도와 밀도가 다른 평행 운동을 하는 두 유체는 모든 속도에 대해 단파장 섭동으로 불안정한 인터페이스를 생성합니다. 그러나 표면 장력은 임계 속도까지 단파장 불안정성을 안정화시킬 수 있습니다.

밀도와 속도가 공간에서 연속적으로 변하면 (유체가 RT-안정적일 수 있도록 가장 가벼운 층을 사용하여) 켈빈-헬름홀츠 불안정성의 역학은 테일러-골드스타인 방정식에 의해 설명됩니다.

서 = g/L ρ {\textstyle N = {\sqrt {/L_{\rho}}}는 Brunt–Väisälä 주파수, U는 수평 평행 속도, k는 파수, c는 문제의 고유값 매개변수, ϕ ~ {\displaystyle {\tilde {\phi}}는 스트림 함수의 복소 진폭입니다. Richardson 번호 \ {Ri의해시작됩니다 일반적으로 레이어는 < 0 <0에 대해 불안정합니다 이러한 효과는 클라우드 레이어에서 일반적입니다. 이러한 불안정성에 대한 연구는 플라즈마 물리학, 예를 들어 관성 구속 융합 및 플라즈마-베릴륨 계면에 적용할 수 있습니다. 낮은 유체보다 더 무거운 유체가 발견되는 정적 안정 상태가 있는 경우, 레일리-테일러 불안정성은 켈빈-로 무시될 수 있습니다.조건을 감안하면 헬름홀츠 불안정성은 충분합니다.[clarification needed]

수치상으로는 켈빈-헬름홀츠 불안정성은 시간적 또는 공간적 접근 방식으로 시뮬레이션됩니다. 시간적 접근에서 흐름은 평균 속도로 "움직이는" 주기적(순환적) 상자에서 고려됩니다(절대 불안정성). 공간 접근 방식에서 시뮬레이션은 자연 유입 및 유출 조건(대류 불안정성)을 가진 실험실 실험을 모방합니다.

2010년 4월 8일 촬영된 태양 대기의 KH 불안정.[1][4]

발견과 역사

켈빈-헬름홀츠 불안정성의 존재는 1868년 독일의 생리학자이자 물리학자인 헤르만 폰 헬름홀츠에 의해 처음 발견되었습니다. 헬름홀츠는 "유체가 흐르는 모든 완벽한 기하학적으로 날카로운 가장자리는 그것을 아래로 찢고 분리 표면을 확립해야 한다"고 확인했습니다.[5][3] 그 후 1871년, 공동 연구자 윌리엄 톰슨(훗날 켈빈 경)은 해상 풍파의 형성을 모델링하는 과정에서 선형 불안정성의 수학적 해결책을 개발했습니다.[6]

켈빈-헬름홀츠 불안정성의 아이디어는 20세기 초에 걸쳐 다양한 층화 유체 응용 분야에 적용되었습니다. 1920년대 초, 루이스 프라이 리처드슨(Lewis Fry Richardson)은 이러한 전단 불안정성이 리처드슨 번호에 캡슐화된 계층화로 인해 전단이 정적 안정성을 극복한 곳에서만 형성된다는 개념을 개발했습니다.

켈빈-헬름홀츠 불안정에 대한 지구물리학적 관측은 1960년대 후반부터 1970년대 초반까지 이루어졌으며,[7] 구름과 그 후 바다를 대상으로 이루어졌습니다.

하트포드 코네티컷 상공의 켈빈-헬름홀츠 구름 형성

참고 항목

메모들

  1. ^ a b Fox, Karen C. (30 December 2014). "NASA's Solar Dynamics Observatory Catches "Surfer" Waves on the Sun". NASA-The Sun-Earth Connection: Heliophysics. NASA.
  2. ^ Sutherland, Scott (March 23, 2017). "Cloud Atlas leaps into 21st century with 12 new cloud types". The Weather Network. Pelmorex Media. Retrieved 24 March 2017.
  3. ^ a b Drazin, P. G. (2003). Encyclopedia of Atmospheric Sciences. Elsevier Ltd. pp. 1068–1072. doi:10.1016/B978-0-12-382225-3.00190-0.
  4. ^ Ofman, L.; Thompson, B. J. (2011-06-01). "SDO/AIA Observation of Kelvin-Helmholtz Instability in the Solar Corona". The Astrophysical Journal. 734: L11. arXiv:1101.4249. doi:10.1088/2041-8205/734/1/L11. ISSN 0004-637X.
  5. ^ Helmholtz (1 November 1868). "XLIII. On discontinuous movements of fluids". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 36 (244): 337–346. doi:10.1080/14786446808640073.
  6. ^ Matsuoka, Chihiro (2014-03-31). "Kelvin-Helmholtz Instability and Roll-up". Scholarpedia. 9 (3): 11821. doi:10.4249/scholarpedia.11821. ISSN 1941-6016.
  7. ^ Ludlam, F. H. (October 1967). "Characteristics of billow clouds and their relation to clear-air turbulence". Quarterly Journal of the Royal Meteorological Society. 93 (398): 419–435. Bibcode:1967QJRMS..93..419L. doi:10.1002/qj.49709339803.
  8. ^ Woods, J. D. (18 June 1968). "Wave-induced shear instability in the summer thermocline". Journal of Fluid Mechanics. 32 (4): 791–800. Bibcode:1968JFM....32..791W. doi:10.1017/S0022112068001035. S2CID 67827521.

참고문헌

  • Lord Kelvin (William Thomson) (1871). "Hydrokinetic solutions and observations". Philosophical Magazine. 42: 362–377.
  • Hermann von Helmholtz (1868). "Über discontinuierliche Flüssigkeits-Bewegungen [On the discontinuous movements of fluids]". Monatsberichte der Königlichen Preussische Akademie der Wissenschaften zu Berlin. 23: 215–228.
  • 심해에서 K-H파의 발견을 설명하는 기사:

외부 링크

위키미디어 커먼즈에는 켈빈-헬름홀츠 파동과 관련된 미디어가 있습니다.