카르노 지도

Karnaugh 지도 예시. 이 이미지는 실제로 두 개의 Karnaugh 지도를 보여준다: ƒ 기능에 대해서는 minterms(색 사각형)를 사용하고, 그 보완에 대해서는 maxterms(회색 사각형)를 사용한다. 이미지에서 E()는 m

{\

로 표시된 minterms의 합계를 나타낸다

\sum m_{i}

Karnaugh map(KM 또는 K-map)은 부울 대수표현을 단순화하는 방법이다. 모리스 카노가 1953년^[1]^[2] 에드워드 W의 정제라고 소개했다. 1952년 Veitch의 Veitch 도표는 앨런 마퀀드의 1881년 논리 다이어그램^[5](일명 마퀀드 도표^[4])을 재발견했지만 지금은 회로 전환에 대한 효용성에 초점을 맞추고 있다.^[3]^[4]^[4] 따라서 Veitch 차트는 Marquand-Vitch 도표로도 알려져 있으며,^[4] Karnaugh 지도는 Karnaugh-Vitch 지도(KV 지도)로도 알려져 있다.

Karnaugh 지도는 인간의 패턴 인식 능력을 이용하여 광범위한 계산의 필요성을 감소시킨다.^[1] 그것은 또한 잠재적인 경주 조건의 신속한 식별과 제거를 허용한다.

필요한 부울 결과는 진실 표에서 2차원 그리드로 전달되며, 카노 지도에서 셀은 그레이 코드로 정렬되며,^[6]^[4] 각 셀 위치는 입력 조건의 하나의 조합을 나타낸다. 각 셀 값은 부울 함수의 해당 출력 값을 나타내는 반면, 셀은 최소값이라고도 한다. 1초 또는 0의 최적 집단이 확인되는데, 이는 원래의 진리표에서 논리의 표준적 형태의 용어를 나타낸다.^[7] 이 용어들은 필요한 논리를 나타내는 최소한의 부울 식을 쓰는 데 사용될 수 있다.

Karnaugh 맵은 최소한의 논리 관문을 사용하여 구현될 수 있도록 실제 논리 요건을 단순화하는 데 사용된다. 제품 총량 표현식(SOP)은 항상 수술 게이트에 공급되는 AND 게이트를 사용하여 구현될 수 있으며, 총량 표현식(POS)은 수술 게이트에 공급되는 수술 게이트로 이어진다. POS 표현식은 함수의 보완점을 제공한다(F가 함수를 의미하므로 그 보완물은 F'^[8]가 될 것이다). Karnaugh 지도는 또한 소프트웨어 설계에서 논리 표현을 단순화하는 데 사용될 수 있다. 예를 들어 조건문에서 사용되는 부울 조건은 매우 복잡해질 수 있으며, 따라서 코드를 읽고 유지하기 어렵게 된다. 일단 최소화되면, AND 및 OR 로직 연산자를 사용하여 표준적인 제품 합과 합산 표현을 직접 구현할 수 있다.^[9]

예

Karnaugh 지도는 부울 대수 함수의 단순화를 용이하게 하기 위해 사용된다. 예를 들어, 다음 진실 표에서 설명하는 부울 함수를 생각해 보십시오.

함수의 진실 표
	A	B	C	D	$f(A,B,C,D)$
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

다음은 부울 변수 $A$ , $B$ , $C$ , $D$ 와 그 반대로 동일한 함수를 비증정 부울 대수에서 설명하는 두 개의 다른 표기법이다.

$f(A,B,C,D)=\sum _{}m_{i},i\in \{6,8,9,10,11,12,13,14\}$ where $m_{i}$ are the minterms to map (i.e., rows that have output 1 in the truth table).
$f(A,B,C,D)=\prod _{}M_{i},i\in \{0,1,2,3,4,5,7,15\}$ where $M_{i}$ are the maxterms to map (i.e., rows that have output 0 in the truth table).

Torus에 그려진 K-map과 평면에 그려진 K-map 점으로 표시된 세포는 인접해 있다.

K맵 구성. 출력 값(진리표에서 가장 오른쪽 값) 대신 이 도표는 입력 ABCD(진리표에서 가장 왼쪽 값)의 십진수 표현을 나타내므로 Karnaugh 지도가 아니다.

3차원에서는 직사각형을 토러스 모양으로 구부릴 수 있다.

건설

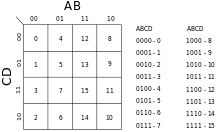
위의 예에서 4개의 입력 변수를 16개의 다른 방법으로 조합할 수 있으므로 진리표는 16개의 행이 있고, 카노우 지도는 16개의 위치가 있다. 따라서 Karnaugh 지도는 4 × 4 격자로 배열된다.

행과 컬럼 지수(카르노 지도 왼쪽 위와 아래에 표시)는 이진수 순서가 아닌 그레이 코드로 정렬된다. 회색 코드는 인접한 셀의 각 쌍 사이에서 오직 하나의 변수만 변화하도록 보장한다. 완성된 Karnaugh 지도의 각 셀은 입력 조합에 대한 함수의 출력을 나타내는 이진 숫자를 포함한다.

그룹화

Karnaugh 지도가 만들어진 후, 그것은 진리표에서 정보를 위해 가능한 가장 간단한 형태 중 하나인 표준 형태를 찾는 데 사용된다. Karnaugh 지도에서 인접한 1s는 표현을 단순화할 수 있는 기회를 나타낸다. 최종 표현식의 최소 용어('최소 용어')는 지도에서 1초의 그룹을 포위하여 찾을 수 있다. 민기 그룹은 직사각형이어야 하며 두 개의 힘(즉, 1, 2, 4, 8...)인 영역을 가져야 한다. 최소 직사각형은 0을 포함하지 않고 가능한 한 커야 한다. 집단은 각각의 집단을 더 크게 만들기 위해 겹칠 수 있다. 아래 예에서 최적의 그룹화는 녹색, 빨간색, 파란색 선으로 표시되며 빨간색과 녹색 그룹이 겹친다. 빨간색 그룹은 2 x 2 제곱이고, 녹색 그룹은 4 x 1 직사각형이며, 겹치는 부분은 갈색이다.

셀은 종종 셀이 커버하는 입력의 논리적 가치를 설명하는 속기로 표시된다. 예를 들어 $AD$ 는 $A$ 와 $D$ 가 참인 2x2 영역을 커버하는 셀을 의미하며, 즉 위의 다이어그램에서 13, 9, 15, 11번으로 번호가 매겨진 셀을 의미한다. 반면에 $AD$ 는 $A$ 가 참이고 $D$ 가 거짓인 세포( $즉$ D가 참이다)를 의미할 것이다.

그리드는 가장자리를 가로질러 직사각형 그룹이 감길 수 있다는 것을 의미한다(그림 참조). 맨 오른쪽의 셀은 해당 입력 값이 단지 1비트씩만 다르다는 점에서 사실상 왼쪽 끝에 있는 셀과 '인접'되어 있다. 마찬가지로 맨 위에 있는 셀과 맨 아래에 있는 셀도 마찬가지다. 따라서 $AD$ 는 유효한 용어일 수 있다. 즉, 위에 12와 8을 포함하며 아래쪽에 감아서 10과 14를 포함하도록 한다. 이 용어는 네 모서리를 포함하는 $BD$ 이다.

해결책

두 개의 K맵을 보여주는 다이어그램. 함수 f(A, B, C, D)에 대한 K맵은 minterms에 해당하는 색상의 직사각형으로 표시된다. 갈색 부분은 빨간색 2×2 정사각형과 녹색 4×1 직사각형의 중첩이다. f의 역에 대한 K맵은 최대값에 해당하는 회색 사각형으로 표시된다.

Karnaugh 지도가 생성되고 인접한 1s가 직사각형과 사각형 박스로 연결되면 각 박스 내에서 어떤 변수가 동일하게 유지되는지 조사하여 대수적 분광법을 찾을 수 있다.

빨간색 그룹의 경우:

A는 상자 전체에서 1과 같으며, 따라서 적색 민어의 대수적 표현에 포함되어야 한다.
B는 (1에서 0으로 바뀌는) 같은 상태를 유지하지 않으므로 제외되어야 한다.
C는 변하지 않는다. 항상 0이므로 보완인 NOT-C가 포함되어야 한다. 따라서 $C$ 가 포함되어야 한다.
D는 변하기 때문에 제외된다.

따라서 부울 산물의 총합 표현식의 첫 번째 미니어는 $AC$ 이다.

녹색 그룹의 경우 A와 B는 동일한 상태를 유지하는 반면 C와 D는 변경된다. B는 0이고 포함되기 전에 부정되어야 한다. 그러므로 두 번째 학기는 $AB$ 이다. 녹색 그룹이 빨간색 그룹과 겹치는 것은 허용된다는 점에 유의하십시오.

같은 방법으로, 블루 그룹은 $BCD$ 라는 용어를 제공한다.

각 그룹의 솔루션은 조합된다. 회로의 일반적인 형태는 $A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}$ $A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}$ + $A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}$ 의 + $A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}$ B의 + $A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}$ 의 + B C $A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}$ 의 ${\$ 이다 $A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}$

따라서 카노우 지도는 다음과 같은 단순화를 안내했다.

{\begin}f(A,B,C,D)={}&{\overline{A}BC{\overline{D}+A{\overline{B}\,{\overline{C}\,{\overline{D}+A{\overline{B}\,{\overline{C}D}D+A{{\overline{B}C{\overline{D}+{}\&gt;A{\overline{B}CD+AB{\overline{C}\,{\overline{D}+AB{\overline{C}D+ABC{\overline{D}\\={}&A{\overline{C}+A{\overline{B}+BC{\overline{D}\ended}}}}

부울대수의 공리를 신중하게 적용함으로써 이러한 단순화를 도출할 수도 있었을 것이지만, 그렇게 하는 데 걸리는 시간은 항 수에 따라 기하급수적으로 증가한다.

반비례

함수의 역은 0을 대신 그룹화하여 같은 방법으로 해결된다.^{[note 1]}

반전을 포괄하는 세 가지 항은 모두 다른 색상의 테두리를 가진 회색 상자로 표시된다.

$갈색$ : $A$ B
금: $A$ $C$
파란색: $BCD$

이렇게 하면 다음과 같은 역효과를 얻을 수 있다.

{f(A,B,C,D)}}={\overline {A}\,{\overline {B}+{\overline {A}\,{\overline {C}+BCD

De Morgan의 법칙을 사용하여 합계의 산출물은 다음과 같이 결정할 수 있다.

{\begin{aligned}f(A,B,C,D)&={\overline {\overline {f(A,B,C,D)}}}\\&={\overline {{\overline {A}}\,{\overline {B}}+{\overline {A}}\,{\overline {C}}+BCD}}\\&=\left({\overline {{\overline {A}}\,{\overline {B}}}}\right)\left({\overline {{\overline {A}}\,{\overline {C}}}}\right)\left({\overline {BCD}}\right)\\&=\왼쪽(A+B\오른쪽)\왼쪽(A+C\오른쪽)\왼쪽({\overline {B}+{\overline{C}+{\overline {D}\오른쪽)\ended{aigned}}}}}

신경 쓰지 마

ABCD = 1111에 대한

f(A,B,C,D)

f(A,B,C,D)

f(A,B,C,D)

f(A,B,C,D)

D

){\displaystyle f(A,B,C,D)}

값은 "상관 없음"으로 대체된다. 이것은 녹색 용어를 완전히 제거하고 빨간색 용어를 더 크게 할 수 있게 한다. 또한 파란색 역항은 변화하고 더 커지게 한다.

Karnaugh 지도는 또한 진실 표에 "상관 없음" 조건이 포함되어 있는 기능을 더 쉽게 최소화할 수 있다. "상관 없음" 조건은 설계자가 출력이 무엇인지 상관하지 않는 입력의 조합이다. 따라서 "상관 없음" 조건은 직사각형 그룹에 포함되거나 직사각형 그룹에서 제외될 수 있다. 그것들은 보통 지도에 대시나 X와 함께 표시된다.

오른쪽의 예는 위의 예와 동일하지만 f(1,1,1,1)의 값이 "상관없다"로 대체된다. 이것은 빨간색 용어가 아래로 확장될 수 있게 하고, 따라서 녹색 용어는 완전히 제거한다.

이는 새로운 최소 방정식을 산출한다.

f(A,B,C,D)=A+BC{\overline{D}

첫 번째 용어는 $AC$ 가 아니라 $A$ 에 불과하다는 점에 유의하십시오. 이 경우 Don't care는 용어(녹색 사각형)를 삭제하고, 다른 용어(빨간색 사각형)를 단순화하며, 경주 위험(경주 위험에 대한 다음 절에서 볼 수 있는 노란색 용어 제거)을 삭제했다.

역 대소문자를 다음과 같이 단순화한다.

{f(A,B,C,D)}}={\overline{A}\,{\overline{B}+{\overline {A}\,{\overline {C}+{\overline {A}D

De Morgan의 법칙을 사용하여 합계의 산출물은 다음과 같이 결정할 수 있다.

{\displaystyle{\begin{정렬}(A,B,C,D)&, ={\overline{\overline{f(A,B,C,D)}}}\\&, ={\overline{{\overline{A}}\,{\overline{B}}+{\overline{A}}\,{\overline{C}}+{\overline{A}}\,D}}\\&, =\left({\overline{{\overline{A}}\,{\overline{B}}}}\right)\left({\overline{{\overline{A}}\,{\overline{C}}}}\right)\left(}{\overline{{\overline{A}\,.D}}\right)\\&=\좌측(A+B\우측)\좌측(A+C\우측)\좌측(A+{\overline {D}\우측)\종료{정렬}}}}

인종 위험

제거

Karnaugh 지도는 경주 조건을 탐지하고 제거하는 데 유용하다. 경주 위험은 Karnaugh 지도를 사용하여 발견하기 매우 쉽다. 왜냐하면 지도에서 제한되어 있는 인접하지만 분리된 지역들 사이를 이동할 때 경주 조건이 존재할 수 있기 때문이다. 그러나, 그레이 코딩의 특성상, 인접한 곳에는 위에서 설명한 특별한 정의가 있다 – 실제로 우리는 위, 아래, 옆면을 감싸고 직사각형이 아닌 토러스 위에서 움직이고 있다.

위의 예에서 C가 1이고 D가 0이고 A가 1이고 B가 1에서 0으로 변할 때(파란색 상태에서 녹색 상태로 이동) 잠재적 경주 조건이 존재한다. 이 경우 출력은 1에서 변하지 않는 것으로 정의되지만, 이 전환은 방정식의 특정 용어로 다루어지지 않기 때문에 글리치(출력의 순간적인 0으로의 전환)의 가능성이 존재한다.
동일한 예에서 더 찾기 어려운 두 번째 잠재적 결함이 있다: D가 0이고 A와 B가 모두 1일 때, C가 1에서 0으로 변화한다(파란색 상태에서 적색 상태로 이동). 이 경우 글리치는 지도 위에서 아래로 감싼다.

이 다이어그램에는 인종적 위험이 존재한다.

레이스 위험을 피하기 위해 합의 항이 추가된 위의 다이어그램.

실제로 결함이 발생할지는 구현의 물리적 특성에 따라 달라지며, 이에 대해 걱정할 필요가 있을지는 애플리케이션에 달려 있다. 클록 처리된 논리에서는 논리가 타이밍 데드라인을 충족시키기 위해 원하는 값으로 정해지는 것으로 충분하다. 우리의 예에서, 우리는 정해진 논리를 고려하지 않고 있다.

우리의 경우, $A{\overline {D}}$ $A{\overline {D}}$ 의 ${\$ 를 추가로 사용하면 녹색과 파란색 출력 상태 또는 청색과 적색 출력 상태 사이를 연결하는 잠재적 경주 위험이 제거된다 $A{\overline {D}}$ . 이는 인접한 다이어그램에서 황색 영역(오른쪽 절반의 아래쪽에서 위쪽으로 감싸고 있음)으로 표시된다.

이 용어는 시스템의 정적 논리 측면에서 중복되지만, 그러한 중복성, 즉 합의된 용어는 인종 없는 동적 성능을 보장하기 위해 종종 필요하다.

이와 유사하게, 또 다른 잠재적 경주 위험을 제거하기 위해 역에 ${\overline {A}}D$ 의 ${\overline {A}}D$ ${\overline{A}D$ 를 추가해야 한다 ${\overline {A}}D$ De Morgan의 법칙을 적용하면 f에 대한 총액표현의 또 다른 산출물이 만들어지지만 $\left(A+{\overline {D}}\right)$ ( $'){\$ 의 새로운 요소와 함께 .

2-모듈 맵 예제

다음은 가능한 2변수 2×2 Karnaugh 지도들이다. 각 항목에는 $\sum m()$ ( $\sum m()$ ) $\sum m()$ 의 $\sum m()$ 함수로서 최소 조건이 수록되어 있으며, 경주 위험 없음(이전 섹션 참조) 최소 방정식이 수록되어 있다. minter는 매핑된 변수의 가장 최소한의 표현 형식을 제공하는 표현으로 정의된다. 가능한 모든 수평 및 수직 상호연결 블록이 형성될 수 있다. 이 블록은 2의 검정력 크기(1, 2, 4, 8, 16, 32, ...)여야 한다. 이러한 표현식은 매핑할 이진 표현식에 대한 최소 논리 변수 표현식의 최소 논리 매핑을 생성한다. 여기 한 필드의 블록이 모두 있다.

차트의 하단, 상단, 왼쪽 또는 오른쪽에서 블럭을 계속할 수 있다. 그것은 가변적 최소화를 위해 차트의 가장자리를 넘어서는 범위까지 확장될 수 있다. 각 논리 변수는 각 수직 열과 수평 행에 해당하기 때문이다. k-map의 시각화는 원통형이라고 볼 수 있다. 왼쪽과 오른쪽 가장자리에 있는 필드가 인접하고, 위쪽과 아래쪽이 인접해 있다. 네 변수에 대한 K-맵은 도넛 또는 토러스 모양으로 표시되어야 한다. k맵이 그린 사각형의 네 모서리가 인접해 있다. 5개 변수 이상에는 여전히 더 복잡한 지도가 필요하다.

σm(0), K = 0
σm(1); K = A′B′
σm(2), K = AB′
σm(3), K = A′B
σm(4), K = AB
σm(1,2); K = B′
σm(1,3); K = A′
σm(1,4); K = A′B′ + AB
σm(2,3); K = AB′ + A′B
σm(2,4); K = A
σm(3,4); K = B
σm(1,2,3); K = A' + B′
σm(1,2,4); K = A + B′
σm(1,3,4); K = A′ + B
σm(2,3,4); K = A + B
σm(1,2,3,4); K = 1

참고 항목

대수 정규 형태(ANF)
BDD(Binary Decision Diagraphy Diagraphy Diagram, BDD), 부울 함수의 압축 표현인 데이터 구조
에스프레소 휴리스틱 로직 미니마이저
부울 대수 주제 목록
로직 최적화
Punnett 제곱(1905) 생물학에서 유사한 도표
Quine-McCluskey 알고리즘
리드-뮬러 확장
벤 다이어그램(1880)
절갈킨다항식

메모들

^ 이는 이전에 찾은 함수의 결과 부정과 혼동해서는 안 된다.

참조

^ ^a ^b Karnaugh, 모리스(11월 1953년)[1953-04-23, 1953-03-17]."지도 방법 Combinational 논리 회선의 강지 진동 합성에"(PDF).미국 전기 기술자의 Part1:통신 및 전자입니다. 72(5):593–599. 거래는 반드시 doi:10.1109/TCE.1953.6371932.종이 53-217.2017-04-16에 있는 원본(PDF)에서 Archived..(NB다. 또한 사무엘 H.Caldwell의 짧은 검토가 포함되어 있습니다.)2017-04-16 Retrieved.
^ Curtis, Herbert Allen (1962). A new approach to the design of switching circuits. The Bell Laboratories Series (1 ed.). Princeton, New Jersey, USA: D. van Nostrand Company, Inc. ISBN 0-44201794-4. OCLC 1036797958. S2CID 57068910. ISBN 978-0-44201794-1. ark:/13960/t56d6st0q. (vii+635쪽)(NB). 이 책은 1969년에 진지가 다시 인쇄하였다.)
^ ^a ^b Veitch, Edward Westbrook (1952-05-03) [1952-05-02]. "A Chart Method for Simplifying Truth Functions". Transactions of the 1952 ACM Annual Meeting. ACM Annual Conference/Annual Meeting: Proceedings of the 1952 ACM Annual Meeting (Pittsburgh, Pennsylvania, USA). New York, USA: Association for Computing Machinery (ACM): 127–133. doi:10.1145/609784.609801.
^ ^a ^b ^c ^d ^e ^f ^g Brown, Frank Markham (2012) [2003, 1990]. Boolean Reasoning - The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-42785-0. [1]
^ ^a ^b 마퀀드, 앨런(1881년)."XXXIII:논리 도표에 n제로".그 런던, 에딘버러,과 더블린 철학. Science지의. 5.12(75):266–270. doi:10.1080/14786448108627104..(NB 단단하다. 많은 제2의 자료들을 잘못되게 또는"n조건에 대한 논리 선도에서""n조건에 대한 논리 선도"로 이 일을 언급합니다.)2017-05-15 Retrieved.
^ Wakerly, John F. (1994). Digital Design: Principles & Practices. New Jersey, USA: Prentice Hall. pp. 48–49, 222. ISBN 0-13-211459-3. (NB. 함께 찍은 두 페이지 섹션에는 K-맵에 회색 코드가 표시되어 있다고 되어 있다. 첫 번째 절에는 입력 간 1비트만 변경하는 코드 라벨이 부착되어 있으며, 두 번째 절에는 이러한 코드를 회색 코드라고 한다.)
^ Belton, David (April 1998). "Karnaugh Maps – Rules of Simplification". Archived from the original on 2017-04-18. Retrieved 2009-05-30.
^ Dodge, Nathan B. (September 2015). "Simplifying Logic Circuits with Karnaugh Maps" (PDF). The University of Texas at Dallas, Erik Jonsson School of Engineering and Computer Science. Archived (PDF) from the original on 2017-04-18. Retrieved 2017-04-18.
^ Cook, Aaron. "Using Karnaugh Maps to Simplify Code". Quantum Rarity. Archived from the original on 2017-04-18. Retrieved 2012-10-07.

추가 읽기

Katz, Randy Howard (1998) [1994]. Contemporary Logic Design. The Benjamin/Cummings Publishing Company. pp. 70–85. doi:10.1016/0026-2692(95)90052-7. ISBN 0-8053-2703-7.
Vingron, Shimon Peter (2004) [2003-11-05]. "Karnaugh Maps". Switching Theory: Insight Through Predicate Logic. Berlin, Heidelberg, New York: Springer-Verlag. pp. 57–76. ISBN 3-540-40343-4.
Wickes, William E. (1968). "3.5. Veitch Diagrams". Logic Design with Integrated Circuits. New York, USA: John Wiley & Sons. pp. 36–49. LCCN 68-21185. p. 36: […] a refinement of the Venn diagram in that circles are replaced by squares and arranged in a form of matrix. The Veitch diagram labels the squares with the minterms. Karnaugh assigned 1s and 0s to the squares and their labels and deduced the numbering scheme in common use.
Maxfield, Clive "Max" (2006-11-29). "Reed-Muller Logic". Logic 101. EE Times. Part 3. Archived from the original on 2017-04-19. Retrieved 2017-04-19.
Lind, Larry Frederick; Nelson, John Christopher Cunliffe (1977). "Section 2.3". Analysis and Design of Sequential Digital Systems. Macmillan Press. ISBN 0-33319266-4. (일반 페이지)
Holder, Michel Elizabeth (March 2005) [2005-02-14]. "A modified Karnaugh map technique". IEEE Transactions on Education. IEEE. 48 (1): 206–207. doi:10.1109/TE.2004.832879. eISSN 1557-9638. ISSN 0018-9359. S2CID 25576523. [2]
Cavanagh, Joseph (2008). Computer Arithmetic and Verilog HDL Fundamentals (1 ed.). CRC Press.
Kohavi, Zvi; Jha, Niraj K. (2009). Switching and Finite Automata Theory (3 ed.). Cambridge University Press. ISBN 978-0-521-85748-2.

외부 링크

Herbert Glarner에 의해 겹치는 직사각형을 감지하십시오.
Karnaugh 지도를 실제 응용에 사용하여, 신호등을 제어하는 회로 설계 프로젝트.
2,3,4 및 5 변수에 대한 K-Map 자습서
Karnaugh 지도 예제
포켓-PC 부울 기능 단순화, 레디온 비틴카 — 조지 E. 안토니우
K-Map 문제 해결

[10] 이는 이전에 찾은 함수의 결과 부정과 혼동해서는 안 된다.

[Karnaugh_1953-1] Karnaugh, 모리스(11월 1953년)[1953-04-23, 1953-03-17]."지도 방법 Combinational 논리 회선의 강지 진동 합성에"(PDF).미국 전기 기술자의 Part1:통신 및 전자입니다. 72(5):593–599. 거래는 반드시 doi:10.1109/TCE.1953.6371932.종이 53-217.2017-04-16에 있는 원본(PDF)에서 Archived..(NB다. 또한 사무엘 H.Caldwell의 짧은 검토가 포함되어 있습니다.)2017-04-16 Retrieved.

[Curtis_1962-2] Curtis, Herbert Allen (1962). A new approach to the design of switching circuits. The Bell Laboratories Series (1 ed.). Princeton, New Jersey, USA: D. van Nostrand Company, Inc. ISBN 0-44201794-4. OCLC 1036797958. S2CID 57068910. ISBN 978-0-44201794-1. ark:/13960/t56d6st0q. (vii+635쪽)(NB). 이 책은 1969년에 진지가 다시 인쇄하였다.)

[Veitch_1952-3] Veitch, Edward Westbrook (1952-05-03) [1952-05-02]. "A Chart Method for Simplifying Truth Functions". Transactions of the 1952 ACM Annual Meeting. ACM Annual Conference/Annual Meeting: Proceedings of the 1952 ACM Annual Meeting (Pittsburgh, Pennsylvania, USA). New York, USA: Association for Computing Machinery (ACM): 127–133. doi:10.1145/609784.609801.

[Brown_2012-4] ^ ^a ^b ^c ^d ^e ^f ^g Brown, Frank Markham (2012) [2003, 1990]. Boolean Reasoning - The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-42785-0. [1]

[Marquand_1881-5] 마퀀드, 앨런(1881년)."XXXIII:논리 도표에 n제로".그 런던, 에딘버러,과 더블린 철학. Science지의. 5.12(75):266–270. doi:10.1080/14786448108627104..(NB 단단하다. 많은 제2의 자료들을 잘못되게 또는"n조건에 대한 논리 선도에서""n조건에 대한 논리 선도"로 이 일을 언급합니다.)2017-05-15 Retrieved.

[Wakerly_1994-6] Wakerly, John F. (1994). Digital Design: Principles & Practices. New Jersey, USA: Prentice Hall. pp. 48–49, 222. ISBN 0-13-211459-3. (NB. 함께 찍은 두 페이지 섹션에는 K-맵에 회색 코드가 표시되어 있다고 되어 있다. 첫 번째 절에는 입력 간 1비트만 변경하는 코드 라벨이 부착되어 있으며, 두 번째 절에는 이러한 코드를 회색 코드라고 한다.)

[Belton_1998-7] Belton, David (April 1998). "Karnaugh Maps – Rules of Simplification". Archived from the original on 2017-04-18. Retrieved 2009-05-30.

[Dodge_2016-8] Dodge, Nathan B. (September 2015). "Simplifying Logic Circuits with Karnaugh Maps" (PDF). The University of Texas at Dallas, Erik Jonsson School of Engineering and Computer Science. Archived (PDF) from the original on 2017-04-18. Retrieved 2017-04-18.

[Cook_2012-9] Cook, Aaron. "Using Karnaugh Maps to Simplify Code". Quantum Rarity. Archived from the original on 2017-04-18. Retrieved 2012-10-07.

[1]

[2]

[5]

[4]

[3]

[6]

[7]

[8]

[9]

[note 1]

Search