골든 앵글

기하학에서 황금각은 원주 둘레를 황금비율에 따라 분할하여 만든 두 각 중 작은 각이다. 즉, 원주 전체 둘레에 대한 더 작은 원호 길이 대 더 큰 원호 길이의 비율과 같은 두 개의 호로 된 것이다..

대수학적으로 a+b를 원의 원주가 되게 하고, 길이가 더 긴 a호와 길이가 더 작은 b로 나누어 다음과 같이 한다.

${\displaystyle {\frac {a+b}{a}}}}={\frac{a}{b}}}$

황금각은 길이 b의 작은 호에 의해 하위 각이 된다. 약 137.5077640500378546463487...° OEIS: A096627 또는 라디안 2.3996322972865332... OEIS: A131988.

이름은 금각과 금비 φ의 연결에서 유래한 것으로, 금각의 정확한 값은 다음과 같다.

${\displaystyle 360\left(1-{\frac {1}{\barphi }}\right)=360(2-\barphi )={\barphi ^{2}}=180({\sqrt{5}}}}{\text{di}}}}}}}}}}}}}}}}}}}}}:{\text{\diod}}}}}}}}}}}}}}}}}}}}}}}}}}$

또는

${\displaystyle 2\pi \왼쪽(1-{\frac {1}{\barphi }}\pi(2-\barphi )={\barphi ^{2}}}=\pi(3-{\sqrt{5}}}}{\text{라디안}}},}},}}},}$

여기서 등가치는 황금비율의 잘 알려진 대수적 특성에서 비롯된다.

사인(sine)과 코사인(cosine)은 초월수이기 때문에 직선과 나침반을 이용해 황금각을 구성할 수 없다.^[1]

파생

위의 조건을 감안할 때 황금 비율은 φ = a/b와 같다.

ƒ은 원주의 분수를 황금 각도로, 또는 동등하게 원의 각도 측정으로 나눈 황금 각도로 나눈 값이다.

${\displaystyle f={\frac {b}{a+b}={\frac {1}{1+\varphi }}.}$

하지만 그 이후로

${\displaystyle {1+\varphi }=\varphi ^{2},}$

그 뒤를 잇다

${\displaystyle f={\frac {1}{\barphi ^{2}}$

이는 φ ² 황금 각도가 원 안에 들어갈 수 있다는 말과 맞먹는다.

따라서 황금 각도가 차지하는 원의 분율은 다음과 같다.

$약 0.381966\,}$

따라서 골든 앵글 g는 다음과 같이 도 단위로 수치 근사치가 될 수 있다.

$(\displaystyle g\reason 360\reason 0.381966\ 약 137.508^{\reason },\,})$

또는 다음과 같이 라디안 단위로 표시:

$2\displaystyle g\ 약 2\pi \cHB 0.381966\ 약 2.3996\,}$

자연의 황금각

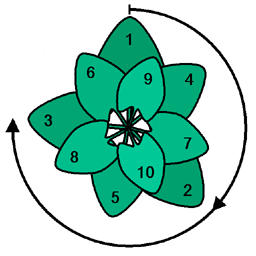
황금각은 식물성 이론에 중요한 역할을 한다. 예를 들어, 황금각은 해바라기의 플로어를 분리하는 각이다.^[2] 패턴 분석 결과 피보나치 각도가 최적의 패킹 밀도를 가진 파라스티치를 제공하는 등 개별 원초도를 분리하는 각도에 매우 민감하다는 것을 알 수 있다.^[3]

플뢰트 개발을 위한 그럴듯한 물리적 메커니즘의 수학적 모델링은 평면의 비선형 부분 미분 방정식의 해법에서 자연적으로 발생하는 패턴을 보여주었다.^[4][5]

참조

외부 링크

위키미디어 커먼즈에는 골든 앵글과 관련된 미디어가 있다.

• 수학계의 골든 앵글