기하학에서 일반화된 헬리코이드는 곡선, 종단 곡선, 그 축을 따라 곡선을 회전하고 동시에 치환함으로써 생성되는 유클리드 공간의 표면이다.주어진 곡선의 어떤 점이라도 원나선의 시작점이다.종단 곡선이 축을 통과하는 평면에 포함되는 경우 일반화된 헬리코이드의 자오선이라고 한다.일반화된 헬리코이드의 간단한 예는 헬리코이드들이다.헬리코이드의 자오선은 직교로 축을 교차하는 선이다.
일반화된 헬리코이드의 필수적인 형태는
- 일반화된 헬리코이드를 지배했다.그들의 종단 곡선은 선이고 표면은 지배적인 표면이다.
- 원형 일반화된 헬리코이드그들의 종단 곡선은 원이다.
수학에서 헬리코이드들은 최소한의 표면으로서 필수적인 역할을 한다.기술 영역에서 일반화된 헬리코이드는 계단, 슬라이드, 나사 및 파이프에 사용된다.
해석적 표현
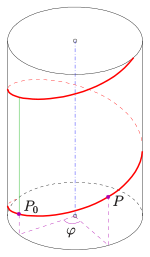
점의 움직임을 방해하다.녹색: 피치,파란색: 나사 축 점의 나사 움직임
나사형 곡선에서 점을 이동한다는 것은 점을 회전하고 선(축)을 따라 이동시켜 변위가 회전 각도에 비례하도록 한다.결과는 원형 나선형이다.
축이 z축인 경우 P =( 0 z ) 의 모션을 파라메트릭 방식으로 설명할 수 있다 .
.

≠ 0을 (를) 경사라고 하고, 각도를 radian으로 측정하며
(를) 경사라고 하고, 각도를 radian으로 측정하며 = c 피치
= c 피치 (녹색)라고 한다.점의 흔적은 원형나선(빨간색)이다.그것은 오른쪽 원형 실린더의 표면에 포함되어 있다.그것의 반지름은 지점 P 의 z축까지의
(녹색)라고 한다.점의 흔적은 원형나선(빨간색)이다.그것은 오른쪽 원형 실린더의 표면에 포함되어 있다.그것의 반지름은 지점 P 의 z축까지의 거리다.
거리다.
c> 의 경우 나선을 오른손이라고 하고 그렇지 않으면 왼손이라고 한다 (= 의 경우 모션은
(= 의 경우 모션은 z축을 중심으로 회전하는 것이다.
z축을 중심으로 회전하는 것이다.
원곡선의 나사 운동
곡선의 나사 운동

모수적 표현으로 일반화된 헬리코이드를 산출하다.

곡선 = ) )은 원형 나선형이다.
나선형이다.
곡선 ,= ) 는 주어진 프로파일 곡선의 복사본이다 .
.
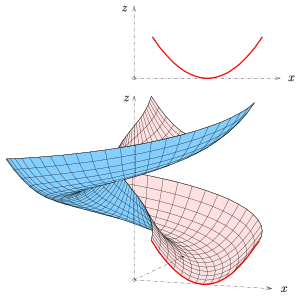
예:위의 첫 번째 그림에서 자오선은 포물선이다.
일반화된 헬리코이드를 지배
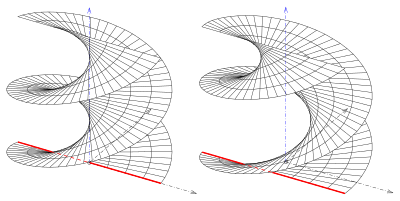
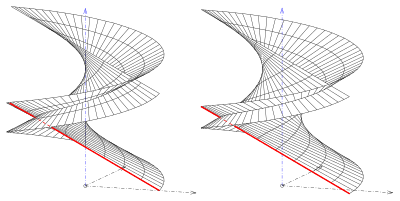
오른쪽 일반화 헬리코이드: 닫힘(왼쪽) 및 열림(오른쪽) 종류들
종단 곡선이 선인 경우 일반화된 헬리코이드를 받는다.네 가지 유형이 있다.
- (1) 직교로 축과 교차한다.하나는 헬리코이드(오른쪽 닫힘으로 일반화된 헬리코이드)를 갖게 된다.
- (2) 선은 축과 교차하지만 직교하지 않는다.사람은 비스듬히 닫힌 활자를 받는다.
주어진 선과 축이 스큐 선인 경우, 열린 유형을 얻게 되며 축이 표면의 일부가 아니다(s. 그림).
- (3) 주어진 선과 축이 스큐 선이고 축에 직교하여 평면에 포함된 경우, 직교형 또는 짧은 시간 내에 열린 헬리코이드를 얻는다.
- (4) 선과 축이 꼬불꼬불하고 선이 ... (s. 3)에 포함되지 않으면 사선형 오픈형이 된다.
사선형은 서로 교차하지만(s. picture), 올바른 형태(헬리코이드)는 교차하지 않는다.
라인이 축에 기울어져 있고 의 거리가 축에 대한 산물이 정확히 c 인 경우 흥미로운 사례를 얻을 수 있다
대한 산물이 정확히 c 인 경우 흥미로운 사례를 얻을 수 있다 이 경우 표면은 접선 개발 가능한 표면이며 다이렉트릭스 sin ) ,d에 의해 생성된다
이 경우 표면은 접선 개발 가능한 표면이며 다이렉트릭스 sin ) ,d에 의해 생성된다 
비고:
- 헬리코이드는 카탈로니아 표면이다.폐쇄형(공통 헬리코이드)은 심지어 코노이드다.
- 일반화된 헬리코이드는 대수학적 표면이 아니다.
폐쇄형 일반 헬리코이드 위에
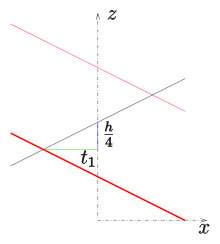
폐쇄된 일반화된 헬리코이드의 자기절개 부분에 대해 폐쇄형 일반 헬리코이드에는 축을 교차하는 종단선이 있다.프로파일 라인이 (, , 0+ t) 1은 다음과 같은 파라메트릭 표현을 얻음
다음과 같은 파라메트릭 표현을 얻음

=  공통 헬리코이드)일 경우 표면이 스스로 교차하지 않는다.
공통 헬리코이드)일 경우 표면이 스스로 교차하지 않는다.
 불꽃형)이 표면과 곡선이 교차하는 경우(표면 위)
불꽃형)이 표면과 곡선이 교차하는 경우(표면 위)
 ,) )및 i= (+ 1), = ,,
,) )및 i= (+ 1), = ,,
이중으로 구성되다무한 이중 곡선이 존재한다. m이(가) 작을수록 이중 곡선 사이의 거리가 커진다.
이중 곡선 사이의 거리가 커진다.
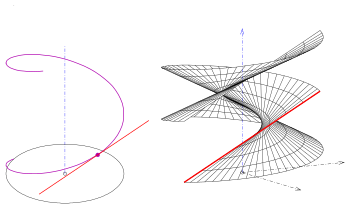
접선 전개식
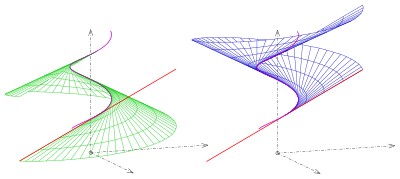
탄젠트 개발 가능: 일반 부품(녹색 및 파란색) 및 다이렉트릭스(직접) 다이렉트릭스(나선)의 경우

탄젠트 개발 가능 표면의 다음과 같은 파라메트릭 표현을 얻는다.

표면 정규 벡터는

= 의 경우 정규 벡터는 null 벡터가 된다.따라서 다이렉트릭스는 단수 점으로 구성된다.다이렉트릭스는 표면의 두 가지 일반적인 부분(s. picture)을 분리한다.
벡터는 null 벡터가 된다.따라서 다이렉트릭스는 단수 점으로 구성된다.다이렉트릭스는 표면의 두 가지 일반적인 부분(s. picture)을 분리한다.
원형 일반화 헬리코이드
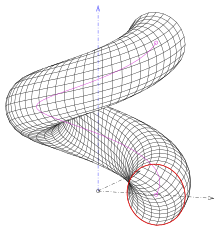
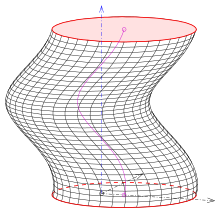
원형 일반화 헬리코이드에는 다음과 같은 3가지 흥미로운 유형이 있다.
- (1) 원형이 자오선이고 축(s. 그림)과 교차하지 않는 경우
- (2) 원을 포함하는 평면은 원 중심부의 나선에 직교한다.파이프 표면을 얻는다.
- (3) 원의 평면은 축과 직교하며, 그 축 점(s. 그림)으로 구성된다.이 활자는 바로크 색채에 사용되었다.
독일 노이엔펠데 성 판크라티우스 제단(16888)
참고 항목
외부 링크
참조
- 엘사 압베나, 시몬 살라몬, 알프레드 그레이:현대적 미분 기하학적 곡선 및 표면 기하학, 3. 에디션, 고급 수학 연구, Chapman & Hall, 2006, ISBN1584884487, 페이지 470
- E. 크라이스치히: 미분 기하학.뉴욕: 도버, 페이지 88, 1991.
- U. Graf, M. Barner: Darstellende Geometrie.퀼 & 마이어, 하이델베르크 1961년 ISBN 3-494-00488-9, 페이지 218
- K. Strubecker: Vorlesungen über Darstellende Geometrie, Vandenhoek & Ruprecht, Götingen, 1967, 페이지 286



 (를) 경사라고 하고,
(를) 경사라고 하고, 
 (녹색)라고 한다.점의 흔적은 원형나선(빨간색)이다.그것은
(녹색)라고 한다.점의 흔적은 원형나선(빨간색)이다.그것은